致远教育集团高三年级2005－2006学年度第二学期联考
数 学 试 卷
一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中只有一项符合题目要求的）
1．已知集合U=R，集合
= （
）
A．
B．
C．
D．
2．若
则下列不等式中一定成立的是
（ ）
A．
B．
C．
D．
3．函数
的反函数是 （
）
A．
B．
C．
D．
4．要得到函数
的图象,只需将函数
的图象作下列平移（ ）
A．按向量
平移 B．按向量
平移
C．按向量
平移 D．按向量
平移
5．
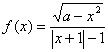为奇函数的充要条件是
（ ）
A．
B．
C．
D．
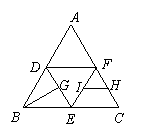6．如图，在正三角形ABC中，D、E、F分别为各边的中点，G、H、I分别为DE、FC、EF的中点，将△ABC沿DE、EF、FD折成三棱锥以后，BG与IH所成角的弧度数为
( )
A．
B．
C．
D．
7．不等式
在
上恒成立，则
的取值范围是 ( )
A．
B．
C．
D．
8．设函数
的最小值为
,最大值为
,设
,则数列｛
｝是
( )
A．公差不为0的等差数列 B．公比不为1的等比数列
C．常数数列 D．不是等差数列，也不是等比数列
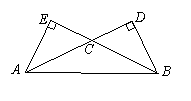9．如图，在△ABC中，
，AC、BC边上的高分别为BD、AE，则以A、B为焦点，且过D、E的椭圆与双曲线的离心率的倒数和为
（ ）
A．
B．1 C．
D．2
10．掷一个骰子的试验，事件A表示“小于5的偶数点出现”，事件B表示“小于4的点数出现”，则一次试验中，事件
发生的概率为
( )
A． B． C． D．
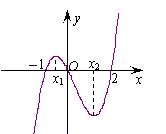11．如图是函数
的大致图象，则
等于
( )
A．
B．
C．
D．
12．从集合
中任选两个元素作为椭圆方程
中的m和n，则能组成落在矩形区域B=
内的椭圆个数为
（ ）
A．43 B．72 C ．80 D．90
二．填空题（本大题共6小题，每小题4分，共24分。把答案填在答题卡相应位置）
13．已知
,则
与
的夹角为 __________.
14．对甲乙两同学的成绩进行抽样分析，各抽取五门功课，得到的观测值如下：
甲：95 100 110 120 125 乙：100 104 110 120 116
那么，两人中各门功课发展较平稳的是__________．
15．圆心为（2，－3），且被直线
截得的弦长为
的圆的标准方程为
．
16．若
， 则
_________________.（用数字作答）
17．已知函数
同时满足五个条件： ①的定义域是［－4,4］；② 
；
③
； ④在［－4,0）上单调递减； ⑤没有最大值.
则不等式
≤0的解集是 _____________________ ．
18．设有四个条件：
①平面
与平面
所成的锐二面角相等；
②直线∥
，
；
③
是异面直线，
且∥
，∥
；
④平面内距离为
的两条平行直线在平面内射影仍为两条距离为的平行直线．
其中能推出∥的条件有
．（把所有正确条件的代号都填上）
三．解答题（本大题共5小题，共60分，解答应写出文字说明、证明过程或演算步骤）.
19．(本小题满分12分，第一小问满分6分，第二小问满分6分)
已知锐角△ABC中，三个内角为A、B、C，两向量
，
，若
与
是共线向量．
（Ⅰ）求∠A的大小；
（Ⅱ）求
取最大值时，∠B的大小．
20. (本小题满分12分)
随着机构改革工作的深入进行，各单位要减员增效，有一家公司现有职员
，（
，且为偶数），每人每年可创利万元.据评估，在经营条件不变的
前提下，每裁员
人，则留岗职员每人每年多创利
万元，但公司需付下岗职员
每人每年
万元的生活费，并且该公司正常运转所需人数不得小于现有职员的
，
为获得最大的经济效益，该公司应裁员多少人？
21．(本小题满分14分，第一小问满分4分，第二小问满分5分,第三小问满分5分)
如图，四棱锥P－ABCD的底面是正方形，PA⊥底面ABCD，PA＝AD＝2，点M、N分别在棱PD、PC上，且PC⊥平面AMN．
(Ⅰ)求证：AM⊥PD；
(Ⅱ)求二面角P－AM－N的大小；
(Ⅲ)求直线CD与平面AMN所成角的大小．
22．(本小题满分14分，第一小问满分4分，第二小问满分4分,第三小问满分6分)
已知双曲线
（
）的右准线
与一条渐近线
交于点P，F是双曲线的右焦点．
（Ⅰ）求证：PF⊥；
（Ⅱ）若PF=3，且双曲线的离心率
，求该双曲线方程；
（Ⅲ）延长FP交双曲线左准线
和左支分别为点M、N，若M为PN的中点,求双曲线的离心率．
23．(本小题满分14分，第一小问满分4分，第二小问满分5分,第三小问满分5分)
已知数列
的前
项和为
，满足：
．
(Ⅰ)当
为何值时，数列是等比数列；
(Ⅱ)在(Ⅰ)的条件下，设数列的公比为
，作数列
使
，求数列的通项公式；
(Ⅲ)在(Ⅱ)条件下，如果对一切
，不等式
恒成立，求实数
的取值范围．
致远教育集团高三年级2006届第二学期数学联考答题纸
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
13． 14． 15．
16． 17． 18．
19．
| |||
 | |||
 | ||||
| ||||
致远中
|
致远教育集团高三年级2005－2006学年度第二学期联考
数学试卷参考答案及评分标准
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | B | A | B | B | A | B | A | A | C | C | C |
13．
14. 乙
15. 
16. 2006
17. 
18. ②③
19．解：(1)=(2－2sinA,cosA+sinA)，=(sinA－cosA,1+sinA)，
∵//
∴（2－2sinA）(1+sinA)－(cosA+sinA)(sinA－cosA)=0; 3分
∵△ABC为锐角形，sinA=
∴A=60° 6分
（2）y=2sin2B+cos(
)=2sin2B+cos
(
)
=2sin2B+cos (2B－60°)
=1－cos2B+cos (2B－60°) =1+sin(2B－30°) 10分
当B=60°时取最大值2 12分
20. 解： 设裁员
人，可获得的经济效益为
万元,
则 
=
4分
依题意 
≥
∴0＜≤
.
又140＜＜420, 70＜＜210. 6分
(1)当0＜
≤,即70＜≤140时，
, 取到最大值; 8分
(2)当＞,即140＜＜210时，
, 取到最大值; 10分
综上所述，当70＜≤140时，应裁员人；
当140＜＜210时，应裁员人.
12分
21．解：(1)PA⊥面ABCD
PA⊥CD又CD⊥AD，∴CD⊥面PAD
∴CD⊥AM，又PC⊥面AMN，∴PC⊥AM
∴AM⊥面PCD，∴AM⊥PD． 4分
(2)PN⊥面AMN，PM⊥AM，∴NM⊥AM，∴∠PMN即为所求．
又∠PMN＝∠PCD，(易证Rt△PNM∽Rt△PDC)，PA＝AD＝2，
∴∠PMN＝arctan． 9分
(3)过M作ME∥CD交PC于E，则∠NME即求．
且∠NME＝∠DPC＝arcsin． 14分
22．解：（1）右准线为x=
，由对称性不妨设渐近线l为y=
x，
则P（
），又F（c，0）， ∴
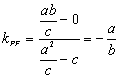， 2分
又∵
，∴kPF·kl =－
=－1，
∴PF⊥l． 4分
（2）∵PF的长即F（c，0）到l:bx－ay=0的距离，
∴
=3，即b=3， 6分
又
， ∴
， ∴a=4，
故双曲线方程为
=1．
8分
（3）PF的方程为：y=－
（x－c），
由
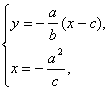得
，
∵M是PN的中点 ∴
，
10分
∵N在双曲线上， ∴
，
即
，
令t=e2，则t2－10t+25=0，∴t=5，即e=
．
14分
23．解．(1)(2＋t)Sn＋1－tSn＝2t＋4 ①
n≥2时，(2＋t)Sn－tSn－1＝2t＋4 ②
两式相减：(2＋t)(Sn＋1－Sn)－t(Sn－Sn－1)＝0，
(2＋t)an＋1－tan＝0，＝．即n≥2时，为常数． 2分
当n＝1时，(2＋t)S2－tS1＝2t＋4，
(2＋t)(a2＋a1)－ta1＝2t＋4，解得a2＝．
要使{an}是等比数列，必须＝．
∴＝，解得a1＝2． 4分
(2)由(1)得，f (t)＝，因此有bn＝，
即＝＋1，整理得＋1＝2(＋1)． 6分
则数列{＋1}是首项为＋1＝2，公比为2的等比数列， 7分
＋1＝2·2n－1＝2n，
bn＝． 9分
(3)把bn＝，bn＋1＝代入得：＋＜，
即c＞＋， 11分
要使原不等式恒成立，c必须比上式右边的最大值大．
∴＋＝＋＝＋＋单调递减．
∴＋的值随n的增大而减小，
则当n＝1时，＋取得最大值4．
因此，实数c的取值范围是c＞4． 14分