培优练习(3)
一、选择题
1、设A、B两点的坐标分别为(-1,0),(1,0),条件甲:![]() ; 条件乙:点C的坐标是方程 + = 1 (y¹0)的解. 则甲是乙的
( )
; 条件乙:点C的坐标是方程 + = 1 (y¹0)的解. 则甲是乙的
( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不是充分条件也不是必要条件
2、长为2的线段PO⊥平面α,O为垂足,A、B是平面α内两动点,若tan∠PAO= ![]() ,
,
tan∠PBO=2,则P点到直线AB的距离的最大值是
( ) A.2![]() cm B.
cm B.![]() cm C.
cm C.![]() cm D.
cm D.![]() cm
cm
3、三个数![]() 成等比数列,若有
成等比数列,若有![]() 成立,则
成立,则![]() 的取值范围是
( )
的取值范围是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、在某次数学测验中,学号![]() 的四位同学的考试成绩
的四位同学的考试成绩![]() ,
,
且满足![]() ,则这四位同学的考试成绩的所有可能情况的种数为
,则这四位同学的考试成绩的所有可能情况的种数为
( )
A.9种 B.5种 C.23种 D.15种
二、填空题
5、已知△ABC中,角A、B、C所对的边分别为a,b,c。若a=1,∠B= 45°,△ABC的面积S=2,那么△ABC的外接圆的直径等于 .
6、已知复数![]() 满足:
满足:![]() ,则
,则![]() __________.
__________.
7、设m、n都是不大于6的自然数,则方程![]() 表示的双曲线的个数是 .
表示的双曲线的个数是 .
8、以下命题:
①二直线平行的充要条件是它们的斜率相等;
②过点(x0,y0)与圆![]() 相切的直线方程是
相切的直线方程是![]() ;
;
③平面内到两定点的距离之和等于常数的点的轨迹是椭圆;
④抛物线上任意一点M到焦点的距离都等于点M到其准线的距离.
其中正确命题的标号是 .
三、解答题
9、(本小题满分12分)
在实数范围内解不等式:![]() 。并利用解此题的方法证明:
。并利用解此题的方法证明:![]() 有唯一解。
有唯一解。
10、(本小题满分12分)
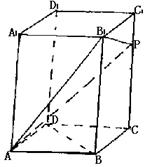
在正四棱柱ABCD—A1B1C1D1中,侧棱是底面边长的2倍,P是侧棱CC1上的任一点.
(1)求证:不论P在侧棱CC1上何位置,总有BD⊥AP;
(2)若CC1=3C1P,求平面AB1P与平面ABCD所成二面角的余弦值;
(3)当P点在侧棱CC1上何处时,AP在平面B1AC上的射影是∠B1AC的平分线.
|
11、(本小题满分14分)
P为椭圆c:![]() 上除
上除![]() ,
,![]() 的两点外的一点。
的两点外的一点。
(Ⅰ)求直线![]() P与
P与![]() 的斜率的乘积;
的斜率的乘积;
(Ⅱ)设P(x,y),求证:![]() ;
;
(Ⅲ)设![]() ,求证:
,求证:![]() 。
。
12、(本小题满分12分)
设数列![]() 是等比数列,
是等比数列,![]() ,公比q是
,公比q是![]() 的展开式中的第二项
的展开式中的第二项
(按x的降幂排列).
(1)用n,x表示通项an与前n项和Sn;
(2)若![]() ,用n,x表示An.
,用n,x表示An.
13、(本小题满分12分)
已知点H(-6,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足![]()
(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过点T(-2,0)作直线l与轨迹C交于A、B两点,若在x轴上存在一点![]() ,
,
使得△AEB是以点E为直角顶点的直角三角形,求直线l的斜率k的取值范围.
14、(本小题满分14分)
对于函数![]() ,若存在实数
,若存在实数![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点.
的不动点.
(1)当a=2,b=-2时,求![]() 的不动点;
的不动点;
(2)若对于任何实数b,函数![]() 恒有两相异的不动点,求实数a的取值范围;
恒有两相异的不动点,求实数a的取值范围;
(3)在(2)的条件下,若![]() 的图象上A、B两点的横坐标是函数
的图象上A、B两点的横坐标是函数![]() 的不动点,
的不动点,
且直线![]() 是线段AB的垂直平分线,求实数b的取值范围.
是线段AB的垂直平分线,求实数b的取值范围.
参考答案
一、选择题 BCDD
二、填空题 5、5 6、 7、16 8、④
三、解答题
9、解:(1)由![]() 得
得![]() ,显然
,显然![]() 是减函数,又当
是减函数,又当![]() 时,
时, ![]() 即
即![]() ;当
;当![]() 时,
时, ![]() ;不等式的解集为
;不等式的解集为![]() .
.
(2)由方程![]() 得,
得, ![]() ,显然函数
,显然函数![]() 是减函数,又当
是减函数,又当![]() 时,
时,![]() ,当
,当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,方程
,方程![]() 有唯一解.
有唯一解.
10、解(1)由题意可知,不论P点在棱CC1上的任何位置,AP在底面ABCD内射影都是AC, ![]() ,
, ![]()
(2)延长B1P和BC,设B1P∩BC=M,连结AM,则AM=平面AB1P∩平面ABCD. 过B作BQ⊥AM于Q,连结B1Q,由于BQ是B1;Q在底面ABCD内的射影,所以B1Q⊥AM,
故∠B1QB就是所求二面角的平面角,依题意,知CM=2B1C1,从而BM=3BC.
所以![]() . 在
. 在![]()
|
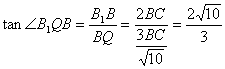 ,
,
![]()
![]() 得
得
![]()
![]() 为所求.
为所求.
(3)设CP=a,BC=m,则BB1=2m,C1P=2m-a,从而![]()
![]()
在![]()
依题意,得![]() .
. ![]() .
.
![]() .
.
即![]()
![]() 故P距C点的距离是侧棱的
故P距C点的距离是侧棱的![]()
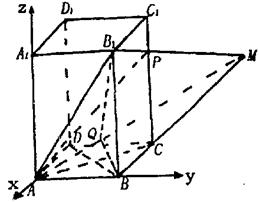
另解:如图,建立空间直角坐标系.
设![]()
![]()
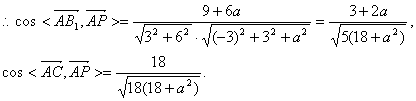
依题意,得![]()
即![]()
故P距C点的距离是侧棱的![]()
11、(Ⅰ)解:设点P(x,y),则有
![]() ,………………………………………………2分
,………………………………………………2分
由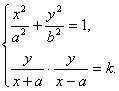 变形为
变形为 ……………………4分
……………………4分
∴![]() 。即
。即![]() 。 ……………………………………5分
。 ……………………………………5分
(Ⅱ)证明:(1)当点P在x轴的上方时,y>0。
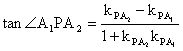 ,
,
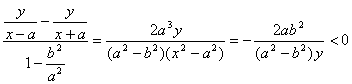 。 …………7分
。 …………7分
(2)当点P在x轴的下方时,y<0,同理可得![]() 。
。
∴![]() 是钝角,
是钝角,![]() …………………………10分
…………………………10分
(Ⅲ)证明:由三角形的面积公式得![]() 。………………12分
。………………12分
![]() 。
。
∴![]() 。
。
得![]()
∴![]() 。 ……………………………………………………14分
。 ……………………………………………………14分
12、解(1)![]()
由![]()
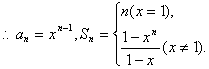
(2)当x=1时,Sn=n, ![]()
又![]()
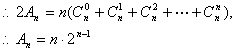
当![]()
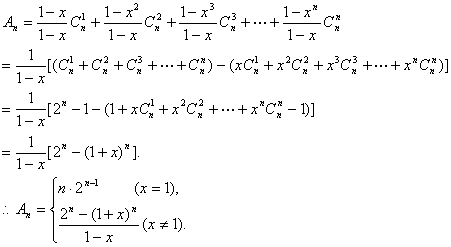
13、解(1)设点M的坐标为![]()
由![]()
由点Q在x轴的正半轴上,得![]() .
.
所以,动点M的轨迹C是以(0,0)为顶点,以(2,0)为焦点的抛物线,除去原点.
(2)设直线![]()
![]()
设![]() 的两个实数根,由韦达定理得
的两个实数根,由韦达定理得
![]() ,
,
所以,线段AB的中点坐标为![]()
而![]()
![]() 轴上存在一点E,使△AEB为以点E为直角顶点的直角三角形,
轴上存在一点E,使△AEB为以点E为直角顶点的直角三角形,
∴点F到x轴的距离不大于![]()
所以 ![]()
化简得![]() ,解之得
,解之得![]() ,结合(*)得
,结合(*)得![]()
又因为直线![]() 的斜率
的斜率![]() 所以
所以![]() ,显然
,显然![]()
故所求直线![]() 的斜率k的取值范围为
的斜率k的取值范围为![]()
14、解![]()
(1)当a=2,b=-2时, ![]()
设x为其不动点,即![]()
则![]()
![]() 的不动点是-1,2.
的不动点是-1,2.
(2)由![]() 得:
得:![]() . 由已知,此方程有相异二实根,
. 由已知,此方程有相异二实根,
![]() 恒成立,即
恒成立,即![]()
即![]() 对任意
对任意![]() 恒成立.
恒成立.
![]()
(3)设![]() ,
,
直线![]() 是线段AB的垂直平分线,
是线段AB的垂直平分线, ![]()
记AB的中点![]() 由(2)知
由(2)知![]()
![]()
化简得: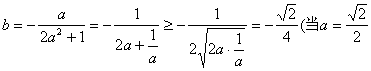 时,等号成立).
时,等号成立).
即![]()
∴ b Î [-,0 ) .