保定市2005--2006年度期末调研考试
数学试题（文史财经类）
命题人：蒋文利 陈云平 冯振好
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分共150分，考试用时120分钟。
（第Ⅰ卷选择题部分，共60分）
一、选择题（本大题共12小题，每个小题5分，共60分，在每小题给出的四个选项中，只有一个是符合要求的）
1、 设集合P=
，Q=
，若P
Q=
，那么
的取值范围是 A 
B 
C 
D
2、0<x<5是不等式x-2<4成立的（ ）
A充分不必要条件 B必要不充分条件 C充要条件 D不充分不必要条件
3、满足f(x)＝f ′(x)的函数是
A．f(x)＝1－x B．f(x)＝x C．f(x)＝0 D．f(x)＝1
4、函数y=
的图象向左平移
个单位，所得的图形对应的函数是
A、偶函数，值域为
B、奇函数，值域为
C、偶函数，值域为 D、奇函数，值域为
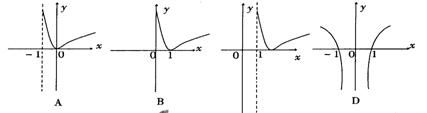
5、函数y= lg（x-1） 的图象是（ ）
|
6、平面上存在两定点M、N，且MN=2,动点P满足
则点P的轨迹是
A、直线 B、线段 C、圆 D、椭圆
7、在数列
中，
（m为非零常数）且前n项和
(k为常数)则
的 值（ ） A、2003 B、2004 C、2005 D、2006
8 直线方程Ax+By=0，若从0，1，2，4，,5，7这六个数字中每次取两个不同的数作为系数A、B的值，则方程表示不同直线的条数是 A．20 B、18 C．14 D．12
9如图已知正方体ABCD－A1B1C1D1，点M、N分别在AB1、BC1上，且AM＝BN．则
①AA1⊥MN；②A1C1∥MN；③MN∥平面A1B1C1D1；④MN与A1C1异面．
以上4个结论中，不正确的结论的个数为
（A）1 （B）2 （C）3 （D）4
10、已知O,A,B三点的坐标分别为O(0,0),A(3,0),
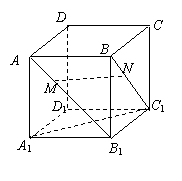B(0,3)。点P在线段AB上，且
(0≤t≤1),
则
的最大值是( )
A.3 B.6 C.9 D.12
11、已知
的值为
A．
B．
C．
ycy D．或
12椭圆
（
）的左右焦点分别为
，若线段
恰好被抛物线
的焦点及顶点四等分，则椭圆的离心率为（ ）
A、
B、
C、
D、
第Ⅱ卷（非选择题部分，共90分）
二、填空题：（本大题共4个小题，每小题4分共16分。把正确的答案填在题后的横线上）
13、某校为了解在校2700名学生的学习情况,从高一、高二、高三各年级采用分层抽样的方法抽取了容量为90的一个样本，已知依次从各年级抽取的人数成等差数列，那么每个学生被抽到的概率及高二年级的学生总数分别为
14、 
的展开式中含
项，则最小自然数n是
.
15、已知O为直角坐标原点，点P在单位圆
上运动，点Q在曲线
(
为参数)上运动，当PQ=
时,
16 已知M（2，-1），N（1，1）A=
,
,O为坐标原点,
，则
最大值为 .
三、解答题：（本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤。）
17、（12分）在同一时间段，由甲乙两个天气预报站，相互独立的对本地天气进行预报，根据以往的统计规律，甲预报站对天气预报的准确率为0.8，乙预报站对天气预报的准确率为0.9
（1）在同一时间段，至少有一个预报站预报准确的
（2）若甲独立预报三次，求甲至多预报一次准确的概率
18. 命题A: 
R, 关于x的方程
有两个非零实数解; 命题B:
R, 关于x的不等式
的解集为空集; 当A、B中有且仅有一个为真命题时, 求实数a的取值范围.
19、已知向量a=(3cos
,sin)
,e=(1,0), 向量a与e的夹角为
.求：tan(
-)的最大值，并求相应的值.
20已知边长为2的菱形ABCD,
BAD=
,AM与边AB、AD所成的角都是
,且AM=
，将
沿BD折起折成直二面角A-BD-
C
，连接
得到几何体MC
-ABD,
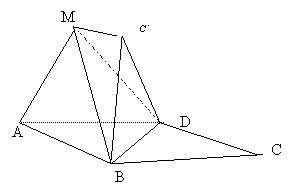(1)求证：MC//平面ABD
（２）求直线CD与BM所成的角.
21、（本题12分）设函数f(x)=x
(x>0)图像上一点(
)的切线交轴于点(
),
（1）求数列
的通项公式(2)设g(n)数列前项的积，求g(n)最大值。
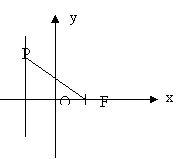
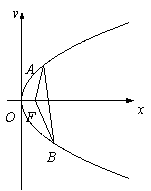
22、已知O为原点, 点P是直线x=-1上一动点,
满足
,
,
(1) 求Q点的轨迹方程
(2)直线 l的方程 y = k(x
–2)与Q点的轨迹交于两点 A、B，设∠AFB = θ，试问 θ 角能否等于 
？若能，求出相应的直线 l 的方程；若不能，请说明理由．
 |
参考答案：
一、选择题：BCCAD CCDBD BD
二、填空题：13、5 14、
、900 15、
16 11
三、解答题：
17, （1）设
A为 “甲预报站预报准确”B为“乙预报站预报准确”则在同一时间段里至少有一个预报准确的概率为
-------4分
（2）P(0)+P(1)=
18、解：对于命题甲：当x>0时， (1-a)x-1=0 即 x=
得 0<a<1；
当x<0时，
(-1-a)x-1=0 即 x=-
得 a>0,要使命题为真命题则有0<a<1；---4分
对于命题乙：当a=1时，显然成立；a=-1是不合题意；当
时不等式的解集为空集的充要条件是
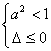解不等式得
--------------10分
由A、B中有且仅有一个为真命题，则
或a=1。---12分
19解；
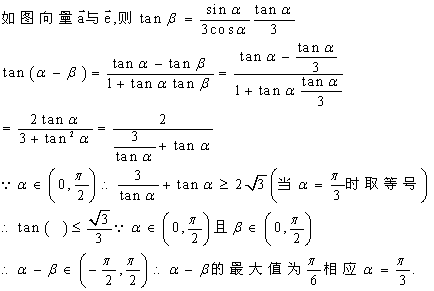
20解：(1)连接AC交于O,连接CO得CO
面ABD,由已知条件MA在面ABD上的射影为<BAD得平分线，过M做MGAo垂足为G, 做GEAB垂足为E,连接ME,
由三垂线定理得连接ME AB，可求得MG=
，因为MG 
Co又COAO
四边形GOCM为矩形M C//面ABD-----6分
(2)由
AMB
AMD得MB=MD
又B C= CD M CBM CD
CM在面MBD上的射影一定在MO上
为H,连接HD,则CDH为
直线CD与平面BMD所成的角;
由(1)知M C面CBD,根据等体积法可求得CH=
,
sin
=
21、（1）设Q
, 由已知得Q点在FP的中垂线上,
即
, 根据抛物线的定义知Q点的轨迹为抛物线.设
所以Q点的轨迹方程为.………4分
(1) 设l方程为 y = k(x – 2)与抛物线 y 2 = 4x 的交点坐标
分别为 A(x1, y1)、B(x2, y2)，假定θ = p，则有 cos θ = －，
如图，即 = － (*) 6分
由
得 ky 2－4y -8 = 0 (k ≠ 0)
得 y1y2 = －8，x1x2 = = 4．
由定义得 AF = x1 + 1， BF = x2 + 1．
从而有 AF 2 + BF 2－ AB 2
= (x1 + 1) 2 + (x2 + 1) 2－(x1－x2) 2－(y1－y2) 2
= －2 (x1 + x2)－6，
AF · BF = (x1 + 1) (x2 + 1)
= x1x2 + x1 + x2 + 1 = x1 + x2 + 5------10分
将代入 (*) 得 = －，
即 x1 + x2 + 1 = 0．
这与 x1 > 0 且 x2 > 0 相矛盾！
所以不能。 12分
22、解
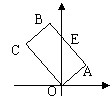
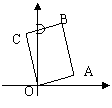（1）
所以四边形OABC为矩形.---3分
(2)当1-2t>0，即0<t<时
直线BC的方程y-2=t(x+2t).
令x=o,y=2t+2，点B在第一象限，
BC与y轴交于点D，
为四边形OABD的面积，
=
-------------6分
当1-2t
0，即t
时，直线AB的方程y-t=-
(x-1).令x=o,y=
，
AB与y轴交于点E, 
-----8分
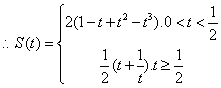---------10分
(3)当 0<t<时，
恒成立。
所以在（0，）内为减函数。
利用单调性定义可证明在[，1]内为减函数，在[1，+
]上为增函数。
所以在（0，1）内为减函数，在[1，+]上为增函数。--------14分