高三百日冲刺·强化训练之《 极限与导数、复数 》
2006. 3
一、选择题：
⒈ 函数在
在
处的切线与直线
平行，则A的值（ ）
A.0 B.1 C.2 D.3
2．如果
为偶函数，且导数存在，则
的值为
（ ）
A.2 B.1 C.0 D.-1
3． 
=
（ ）
A. 
B. 
C. 
D. 
4．已知
，则
等于
（ ）
A.2 B.0 C.-2 D.-4
⒌ 复数
的虚部为
（ ）
A. 
B. 
C. 
D. 
⒍ 若
，则
（ ）
A. 
B. 
C. 
D. 
⒎ 设函数
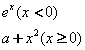为R上的连续函数，则
等于
（ ）
A.-1 B.0 C.1 D.2
⒏ 已知函数
在区间
内单调递减，则实数的取值范围是（ ）
A. 
B. 
C. 
D. 
⒐ 方程
在上
的实根个数为
（ ）
A.1 B.2 C.3 D.4
⒑ 设在点
处可导，、
为非零常数，则
等于 （ ）
A. 
B. 
C. 
D. 
⒒ 函数极限
的值为
（ ）
A. 
B. 
C. 
D. 
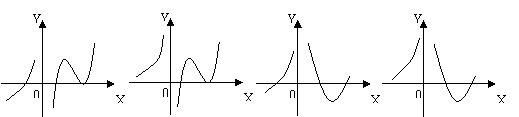
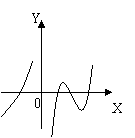
⒓ 设函数在定义域内可导，
的图象如右图所示，则导函数
可能为下列图中所示图象的（ ）
A. B. C. D.
二．填空题：
⒔ 函数
的单调减区间为
。
⒕ 函数
在处有极值10，则
。
⒖ 设
，则
。
⒗ 有如下四个命题：
①
函数
在处连续且
；
②
在
处可导
在处不可导，则
在处一定不可导；
③函数在
内可导且为奇函数，则
为偶函数；
④函数在取得极值，则
，其中正确的命题序号是
。
三．解答题：
⒘ 函数
，当
时，取得极大值8；当
时，有极小值-19，求的表达式。
18．已知曲线
与曲线
交于O、A两点，直线
与曲线
分别交于B、D。
⑴写出四边形ABOD的面积S与
的函数关系
；
⑵讨论
的单调性，并求的最大值。
19．已知曲线
，曲线
，直线
与都有相切，求直线的方程。
⒛ ⑴证明：对任意正数，有不等式
⑵若
,且
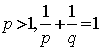，求证：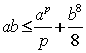
21．已知抛物线
，过C上点M，且与M处的切线垂直的直线称为C在点M的法线。
⑴若C在点M的法线的斜率为
，求点M的坐标（
）；
⑵设
为C对称轴上的一点，在C上是否存在点，使得C在该点的法线通过点P？若有，求出这些点，以及C在这些点的法线方程；若没有，请说明理由。
22．设函数
⑴证明
，其中
为整数
⑵设为的一个极值点，证明
⑶设在
内的全部极值点按从小到大的顺序排列为
，证明
极限与导数、复数参考答案
一、选择题：
1.B 2.C 3.A 4.D 5.B 6.C 7.D 8.B 9.A 10.C 11.B 12.D
二、填空题：
13. 
14. 4 15. 
16. ③
三、解答题：
17.依题意，有
，
在
内是减函数，
且
，
又
，
，
，故
。
18.（1）由方程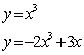 
得交点 
又
（2）
令
19.设直线
与
的切点分别为
，
又
或
， 
的方程为：
或 
。
20.（1）讨论函数
在区间
上的最大值，
，令
，将区间分成两个区间
与
，
列表：
|
| 1 |
| |
|
|
| 0 |
|
|
|
| 极大值点 |
|
故当
时，
有最大值，又
，
。
（2）在不等式
中，令
有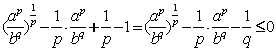
不等式两端乘以
，有
，
。
21.(1) 
的导数
上点
处切线的斜率
，因过点的法线斜率为
，所以
，解得
，故点M的坐标为
。
（2）设
为C上一点，①若
，则C上点
处的切线斜率
，过点的法线方程为
，此法线过点
；②若
，则过点的法线方程为：
①
若法线过，则
，即 
②
若
，则
，从而
，将上式代入①，
化简得：
，
若
与矛盾，若
，则②式无解。
综上，当时，在C上有三点
及
，在这三点的法线过，其方程分别是：
。
当
时，在C上有一点，在这点的法线过点，其方程为：。
22.（1）由函数的定义，对任意整数
，有
，
（2）函数在R上可导：
①
令，得
，此方程一定有解，的极植点
一定满足
，由
得
，
。
（3）设
，是的任意正实根，即，
则存在一个非负整数，使
，即在第二或第四象限内，由①式，
在第二或第四象限中的符号可列表如下：
|
|
|
|
| |
|
|
|
| 0 |
|
|
|
| 0 |
| |
所以，满足的正根都为的极值点，由题设条件，
为方程
的全部正实根，且满足
，那么对于
，
②
由于
，
，
，
由于
，由②式知
，
由此综上，
。