2006年高三第一轮单元练习
数学学科 撰稿：黄冈 刘杰峰 张峰
第一单元 <<集合与简易逻辑>>
一.选择题:
1．如果C、R和I分别表示复数集、实数集和纯虚数集，其中C是全集。则有( )
A. C=R∪I
B. R∩I=｛0｝
C. R∩I=
D. ＣcR=C∩I
2．集合M=
，且
.则实数a的取值范围是( )
A. a
-1 B.
a1 C. a
-1 D.a1
3．满足｛a，b｝UM=｛a，b，c，d｝的所有集合M的个数是（ ）
A. 7 B. 6 C. 5 D. 4
4．a
R,
<3成立的一个必要不充分条件是（ ）
A. a<3 B. <2 C. 
<9
D. 0<a<2
5．若命题P：xA
B
，则
P是（ ）
A. x
A
B B. xA或xB C. xA且xB D. xAB
6．已知集合M=｛,a｝.P=｛-a,2a-1｝；若card(MP)=3，则MP= ( )
A.｛-1｝ B.｛1｝ C.｛0｝ D.｛3｝
7．设集合P=｛3,4,5｝.Q=｛4,5,6,7｝.定P*Q=
，则P*Q中元素的个数是 ( )
A. 3 B. 7 C. 10 D. 12
8．不等式
<0的解集为全体实数，则实数a的取值范围是 ( )
A. 
<a<1
B. <a1 C. a1
D.a<-1或a>1
9．用反证法证明：“若mZ且m为奇数，则
均为奇数”，其假设正确的是 ( )
A. 都是偶数 B. 都不是奇数 C. 不都是奇数 D. 都不是偶数
10．命题P:若a.bR，则
>1是
>1的充分而不必要条件：命题q:函数
的定义域是
.则 （ ）
A.“ p或q”为假 B. “p且q”为真 C. p真q假 D. p假q真
11．若集合
,
，满足=A，则称(,) 为集合A的一种分析，并规定：当且仅当=时，(,)与(,)为集合A的同一种分析，则集合的A=
不同分析种数是 ( )
A. 27 B. 26 C. 9 D. 8
12．50名学生参加跳远和铅球两项测验，跳远和铅球两项及格的分别是40人和31人，两项均不及格的有4人，两项测验部分都及格的人数是 （ ）
A. 35 B. 25 C. 28 D. 15
选择题答题卡：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二．填空题：
13．设A=｛1，2｝，B=｛x｜x
A｝若用列举法表示，则集合B是
14．若不等式
和
>0均不成立，则a的取值范围是
15．含有三个实数的集合可表示为
，则
16．以下命题：①“菱形的两条对角线互相平分”的逆命题；②
或｛0｝
；③对于命题p且q,若p假q真,则p且q为假；④有两条相等且有一个角是
“是”一个三角形为等边三角形的充要条件。其中为真命题的序号为
三．解答题：
17．已知全集u=R，且
，求
18．解关于x的不等式：
（理）（ax-1）(x-1)>0 （文）(x-1)(x-a)>0
19．已知命题p:
有两个不相等的负数根；命题q:方程
无实根，若“p或q”为真，而“p且q”为假，求实数m的取值范围。
20．已知集合
,且
，求a,b的值
21．已知不等式
⑴若对于所有实数x，不等式恒成立，求m的取值范围
⑵若对于m[-2,2]不等式恒成立，求x的取值范围
22．对于函数
，若=x，则称x为的“不动点”；若
，则称x为 “稳定点”，函数的“不动点”和“稳定点”的集合分别记为A和B，既
.
⑴求证：AB
⑵若
，且
,求实数a的取值范围.
参 考 答 案
一. 集合与简单逻辑
一.选择题:
1.C 2.C 3.D 4.A 5.B 6.B 7.D 8.B 9.C 10.D 11.A 12.B
二.填空题:
13. 
14.
15.-1
16.② ③ ④
三.解答题:
17.
∴
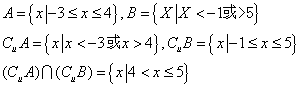
18.(理)当a<0时,不等式的解集为
当a=0时,原不等式的解集为
当0<a<1时,原不等式的解集为
当a1时,原不等式的解集为
(文)当a<1时,原不等式的解集为
当a1时,原不等式的解集为
19.命题p为真时,
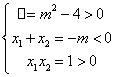
所以m>2,
命题q为真是,
又∵“p或q”为真 “p且q”为假
∴p,q必为一真一假, ∴1<m2或3m
20. 
∵
∴
中元素必是B的元素
又∵
, ∴
中的元素属于B,
故
而
.
∴-1,4是方程
的两根
∴a=-3,b=-4
21.(1)原不等式等价于
对任意实数x恒成立
∴
∴
(2)设
要使
在[-2,2]上恒成立,当且仅当
∴
∴
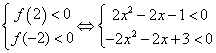
的取值范围是
22.(1)若A=,则AB显然成立,若
则
(t)=t, [(t)]=[t]=t,既tB
从而AB
(2)A中元素是方程
的根，既
的根
由
，∴
或既
B中元素是方程
既
的根
由
，则方程可化为
要使A=B，既使方程
①/无实根，
或实根是方程
②/的根
若①无实根，则
解得
若②有实根，且①的实根是②的实根，由②有
代入①得
，由此解得
，再代入②得
∴
故a的取值范围是