江苏省成化高中06届高三第四次月考数学试卷
(考查范围:全部高中内容)
第Ⅰ卷(选择题 共60分)
一. 选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设![]() 为全集,
为全集,![]() 是
是![]() 的三个非空子集,且
的三个非空子集,且![]() ,则下面论断正确的是
(
)
,则下面论断正确的是
(
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.数列![]() 的前
的前![]() 项和
项和![]() ( )
( )
A.1 B.-1 C. 2 D. -2
3.从6人中选4人分别到南京、无锡、苏州、扬州四个城市游览,要求每个城市有一人游览,每人只游览一个城市,且这6人中甲、乙两人不去南京游览,则不同的选择方案共有 ( )
A.300种 B.240种 C.144种 D.96种
4.“a=b”是“直线![]() ”的 ( )
”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
5.已知![]() ,
,![]()
![]() ,则x,y之间的大小关系是( )
,则x,y之间的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.不能确定
D.不能确定
6.若函数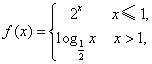 则y=f(1-x)的图象可以是
( )
则y=f(1-x)的图象可以是
( )
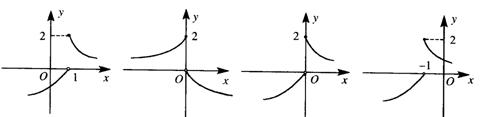
A
B
C
D
7.过抛物线![]() 的焦点作一条直线与抛物线相交于A、B两点,它们的横坐标之和等于5,则这样的直线
( )
的焦点作一条直线与抛物线相交于A、B两点,它们的横坐标之和等于5,则这样的直线
( )
A.有且仅有一条 B.有且仅有两条 C.有无穷多条 D.不存在
8.不共面的四个定点到平面![]() 的距离都相等,这样的平面
的距离都相等,这样的平面![]() 共有 ( )
共有 ( )
A.3个 B.4个 C.6个 D.7个
9.若函数![]() 在区间
在区间![]() 内恒有f(x)>0,则f(x)的单调递增区间为
( )
内恒有f(x)>0,则f(x)的单调递增区间为
( )
A.![]() B.
B. ![]() C. (0,¥) D.
C. (0,¥) D. ![]()
10 ![]() 是定义在R上的以3为周期的偶函数,且
是定义在R上的以3为周期的偶函数,且![]() ,则方程
,则方程![]() =0在区间
=0在区间
(0,6)内解的个数的最小值是 ( )
A.5 B.4 C.3 D.2
11.已知向量![]() ≠
≠![]() ,
,![]() =1,对任意t∈R,恒有
=1,对任意t∈R,恒有![]() -t
-t![]() ≥
≥![]() -
-![]() ,则( )
,则( )
A. ![]() ⊥
⊥![]() B.
B. ![]() ⊥(
⊥(![]() -
-![]() ) C.
) C. ![]() ⊥(
⊥(![]() -
-![]() ) D. (
) D. (![]() +
+![]() )⊥(
)⊥(![]() -
-![]() )
)
12.若三棱锥A-BCD的侧面ABC内一动点P到底面BCD的距离与到棱AB的距离相等,则动点P的轨迹与△ABC组成图形可能是 ( )
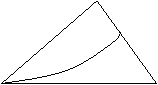 | 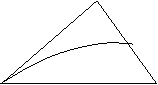 |
|
|
|
|
|
|
|
|
A B
 |  |
|
|
|
|
|
|
|
|
C D
第Ⅱ卷(本卷共12题,共90分)
二.填空题:本大题共6小题,每小题4分,共24分。把答案填在题中横线上.
13.![]() 的展开式中,常数项为
。(用数字作答)
的展开式中,常数项为
。(用数字作答)
 14.如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,则O到平面AB
C1D1的距离为
14.如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,则O到平面AB
C1D1的距离为
15.已知单调函数y=f(x)的定义域是[0,2],且![]() ,那么函数
,那么函数![]() 的定义域是_____________________
的定义域是_____________________
16.函数![]() 的图象与直线
的图象与直线![]() 有且仅有两个不同的交点,则
有且仅有两个不同的交点,则![]() 的取值范围是__________。
的取值范围是__________。
17.已知在△ABC中,∠ACB=90°,BC=3,AC=4,P是AB上的点,则点P到AC、BC的距离乘积的最大值是
18.将1,2,…,9这9个数平均分成三组,则每组的三个数都成等差数列的概率为(用分数作答)
三、解答题:本大题共5小题,满分66分,解答应写出文字说明,证明过程或演算步骤.
19. (本题满分12分)已知向量![]() 和
和![]() ,
,![]() 且
且![]() 求
求![]() 的值.
的值.
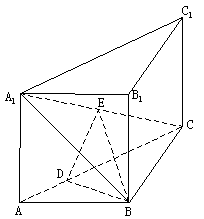
20. (本题满分12分)直三棱柱ABC-A1B1C1中,![]() ,E是A1C的中点,
,E是A1C的中点,![]() 且交AC于D,
且交AC于D,![]() 。 (I)证明:
。 (I)证明:![]() 平面
平面![]() ;
;
(II)求平面![]() 与平面EDB所成的二面角的大小(仅考虑平面角为锐角的情况)。
与平面EDB所成的二面角的大小(仅考虑平面角为锐角的情况)。
21. (本题满分14分)设数列{an}的首项a1=![]() ,且
,且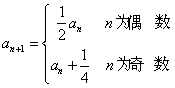 ,
,
记![]() ,n==l,2,3,…·.
,n==l,2,3,…·.
(I)求a2,a3;(II)判断数列{bn}是否为等比数列,并证明你的结论;
(III)求![]() 的表达式。
的表达式。
22. (本题满分14分)已知椭圆C:![]() +
+![]() =1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线l:y=ex+a与x轴.y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
=1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线l:y=ex+a与x轴.y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设![]() =λ
=λ![]() .
.
(Ⅰ)证明:λ=1-e2; (Ⅱ)确定λ的值,使得△PF1F2是等腰三角形.
23. (本题满分14分)函数![]() 的图象上有两点A(0,1)和B(1,0)
的图象上有两点A(0,1)和B(1,0)
(Ⅰ)在区间(0,1)内,求实数a使得函数![]() 的图象在x=a处的切线平行于直线AB; (Ⅱ)设m>0,记M(m,
的图象在x=a处的切线平行于直线AB; (Ⅱ)设m>0,记M(m,![]() ),求证在区间(0,m)内至少有一实数b,使得函数图象在x=b处的切线平行于直线AM.
),求证在区间(0,m)内至少有一实数b,使得函数图象在x=b处的切线平行于直线AM.
06届高三第四次月考数学试卷参考答案
一.选择题:本大题共12小题,每小题5分,共60分.
1.C 2. D 3. B 4. A 5. A 6. C 7. B 8. D 9. D 10. B 11. C 12. D
二.填空题:本大题共6小题,每小题4分,共24分
13. 672 14. ![]() 15.
15. ![]() 16.
16. ![]() 17. 3 18.
17. 3 18. ![]()
三、解答题:本大题共5小题,共66分. 解答应写出文字说明,证明过程或演算步骤.
19.解:![]()
![]() =
=
![]() =
=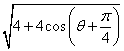 =
=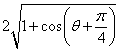
由已知![]() ,得
,得![]() ……… 6分
……… 6分
又![]()
![]()
![]() …… 9分
…… 9分 ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() …… 12分
…… 12分
20.(I)证: ![]() 三棱柱
三棱柱![]() 中
中![]() ,
,
![]() 中
中![]()
![]() 是等腰三角形
是等腰三角形
![]() E是等腰
E是等腰![]() 底边
底边![]() 的中点,
的中点, ![]()
又依条件知![]() 且
且![]()
由①,②,③得![]() 平面EDB ………5分
平面EDB ………5分
(II)解: ![]() 平面
平面![]() , 且
, 且![]() 不平行,
不平行,
故延长![]() ,ED后必相交, 设交点为E,连接EF,如下图
,ED后必相交, 设交点为E,连接EF,如下图
![]() 是所求的二面角 依条件易证明
是所求的二面角 依条件易证明![]()
![]() 为
为![]() 中点,
中点, ![]() A为
A为![]() 中点
中点 ![]()
![]()
![]() 即
即![]() 又
又![]() 平面EFB,
平面EFB, ![]()
![]() 是所求的二面角的平面角 ………10分
是所求的二面角的平面角 ………10分
![]() E为等腰直角三角形
E为等腰直角三角形![]() 底边中点,
底边中点, ![]()
故所求的二面角的大小为![]() ………12分
………12分

21.(I)a2=a1+![]() =1,a3=
=1,a3=![]() a2=
a2=![]() ;………2分
;………2分
(II){bn}是公比为![]() 的等比数列·………4分
的等比数列·………4分
证明如下:
因为bn+1=a2n+1-![]() =
=![]() a2n-
a2n-![]() =
=![]() (a2n-1-
(a2n-1-![]() )=
)=![]() bn, (n∈N*)
bn, (n∈N*)
所以{bn}是首项为![]() , 公比为
, 公比为![]() 的等比数列·………8分
的等比数列·………8分
(III)由(II)知![]() ,所以
,所以![]() ………10分
………10分
![]() =
=![]() ……….14分
……….14分
22.(Ⅰ)证法一:因为A、B分别是直线l:![]() 与x轴、y轴的交点,所以A、B的坐标分别是
与x轴、y轴的交点,所以A、B的坐标分别是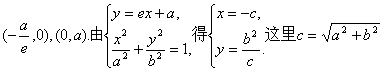 .
.
所以点M的坐标是(![]() ). 由
). 由![]()
即 ………7分
………7分
证法二:因为A、B分别是直线l:![]() 与x轴、y轴的交点,所以A、B的坐标分别是
与x轴、y轴的交点,所以A、B的坐标分别是![]() 设M的坐标是
设M的坐标是![]()
所以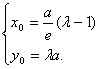 因为点M在椭圆上,所以
因为点M在椭圆上,所以 ![]()
即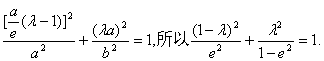
![]() 解得
解得![]()
(Ⅱ)解法一:因为PF1⊥l,所以∠PF1F2=90°+∠BAF1为钝角,要使△PF1F2为等腰三角形,必有PF1=F1F2,即![]()
设点F1到l的距离为d,由![]()
得![]() 所以
所以![]()
即当![]() △PF1F2为等腰三角形. ………14分
△PF1F2为等腰三角形. ………14分
解法二:因为PF1⊥l,所以∠PF1F2=90°+∠BAF1为钝角,要使△PF1F2为等腰三角形,必有PF1=F1F2,
设点P的坐标是![]() ,
,
则
由PF1=F1F2得![]()
两边同时除以4a2,化简得![]() 从而
从而![]()
于是![]() . 即当
. 即当![]() 时,△PF1F2为等腰三角形.
时,△PF1F2为等腰三角形.
23.(Ⅰ)解:直线AB斜率kAB=-1 ![]()
令![]()
解得 ![]() …………………………4分
…………………………4分
(Ⅱ)证明:直线AM斜率 ![]()
考察关于b的方程![]()
即3b2-2b-m2+m=0 ………………7分
在区间(0,m)内的根的情况
令g(b)= 3b2-2b-m2+m,则此二次函数图象的对称轴为![]()
而![]()
g(0)=-m2+m=m(1-m)
g(m)=2m2-m-m(2m-1) ………………10分
∴(1)当![]() 内有一实根
内有一实根
(2)当![]() 内有一实根
内有一实根
(3)当![]() 内有一实根
内有一实根
综上,方程g(b)=0在区间(0,m)内至少有一实根,故在区间(0,m)内至少有一实数b,使得函数图象在x=b处的切线平行于直线AM…………14分