南昌十六中2005-2006年高三周练卷（6）
2005-11-3
一、选择题（本题每小题5分，共60分）
1．
（
）
A.
B.
C.1
D.
2．圆
的右焦点到直线
的距离是（
）
A.
B.
C.1
D.
3．已知函数y＝4 x－3·2 x＋3, 当其值域为[1, 7 ]时, 自变量x的取值范围是( )
A．
B．
C．
∪
D．∪
4．若锐角
终边上一点的坐标为（2sin3,－2cos3），则的值为（ ） A．
B．3 C．
D．
5．为了得到函数
的图象，可以将函数
的图象（ ）
A.向右平移
个单位长度 B．向右平移
个单位长度
C．向左平移个单位长度 D．向左平移个单位长度
6．已知点
在椭圆
上，则
的最大值是（ ）
A．
B．
C．
D．
7．圆心在直线
上，且与两坐标轴都相切的圆的方程为 （ ）
A．
B．
C．
D． 
8．是双曲线
右支上一点，
是右焦点，
是
的中点，
为坐标原点，若
，则点到该双曲线右准线的距离为（ ）
A．
B．
C．
D．6
9．函数f(x)=sinxcosx的图象相邻的两条对称轴间的距离是 （ ）
A．
B．
C．
D．
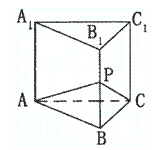
10．如图正三棱柱ABC—A1B1C1底面边长与高相等，截面PAC
把棱柱分成两部分的体积之比为5∶1，则二面角P—AC—B
的大小为 （ ）
A．30° B．45°
C．60° D．75°
11．已知双曲线
的一条渐近线与直线垂直，则该双曲线的离心率是 （ ）
A．
B．
C．
D．
12．若P为双曲线
上的一点，F为一个焦点，以PF为直径的圆与以实轴为直径的圆的位置关系是（ ）
A．相交 B．相切 C．相离 D．以上三种情况均有可能
二、填空题（每小题4分，共16分）
13．已知椭圆
与双曲线
具有相同的焦点F1，F2，设两曲线的一个交点为Q,∠QF1F2＝90°，则双曲线的离心率为
14．双曲线的离心率e=2，则它的一个顶点把焦点之间的线段分成长、短两段的比是 .
15．函数
的最大值等于
16．当
时，函数
的最小值为
三、解答题（共74分）
17．（本小题满分12分）
已知向量a=(1,2),b=(－2,1),k ,t为正实数，向量x=a+(t2+1)b,
y=－ka+
b.
（1） 若x⊥y，求k的最小值；
（2） 否存在k , t ,使x∥y？若存在，求出k的取值范围；若不存在，请说明理由.
18. （本小题满分12分）
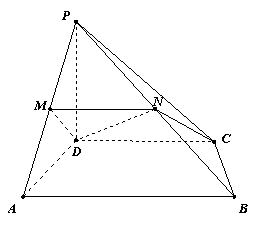
在四棱锥P－ABCD中，AD⊥AB，CD∥AB，PD⊥底面ABCD，
,直线PA与底面ABCD成60°角，点M、N分别是PA、PB的中点．
（1） 求二面角P－MN－D的大小；
（2） 如果△CDN为直角三角形，求
的值．
19．本小题满分12分)
袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为
现有甲、乙两人从袋中轮流摸取1球，甲先取，乙后取，然后甲再取……取后不放回，直到两人中有一人取到白球时既终止，每个球在每一次被取出的机会是等可能的，用
表示取球终止所需要的取球次数.
（I）求袋中原有白球的个数；
（II）求随机变量的概率分布；
（III）求甲取到白球的概率.
20．设M是椭圆
上的一点，P、Q、T分别为M关于y轴、原点、x轴的对称点，N为椭圆C上异于M的另一点，且MN⊥MQ，QN与PT的交点为E，当M沿椭圆C运动时，求动点E的轨迹方程．
21．已知函数f(x)=－x3＋3x2＋ax＋b在x＝(1，f(1))处的切线与直线12x－y－1＝0平行．
（1）求实数a的值；
（2）求f(x)的单调递减区间；
（3） 若f(x)在区间[－2，2]上的最大值为20，求它在该区间上的最小值．
22．已知椭圆C：
＋
＝1（a＞b＞0）的左．右焦点为F1、F2，离心率为e. 直线
l：y＝ex＋a与x轴．y轴分别交于点A、B，M是直线l与椭圆C的一个公共点，P是点F1关于直线l的对称点，设
＝λ
.
（Ⅰ）证明：λ＝1－e2；
（Ⅱ）若
，△PF1F2的周长为6；写出椭圆C的方程；
（Ⅲ）确定λ的值，使得△PF1F2是等腰三角形.
南昌十六中2006届高三数学周考试卷（6） 考试时间：2005-11-03
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 得分 | 17 | 18 | 19 | 20 | 21 | 22 | |||
|
|
|
|
|
|
| ||||
一、选择题答题表：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题答题表：
13、 14、
15、 16、
三、解答题（本题17—21小题每题12分，22小题14分，共74分）
17、(本小题满分12分)
18、(本小题满分12分)
19、(本小题满分12分)
20、(本小题满分12分)
21、(本小题满分12分)
22、(本小题满分14分)
参考答案及部分解答
一、选择题（每小题5分，共60分）：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| D | A | A | C | B | C | A | A | C | A | C | B |
二、填空题（每小题4分，共16分）
13． 
； 14．； 15．
； 16．
三、解答题（共74分，按步骤得分）
17．解：（1）向量x、y的坐标………………2分
列式、整理得
…………5分
由基本不等式求得k的最小值为2…………7分
（2）假设存在正实数k，t，使得x∥y，则
整理，得
……………………12分
满足上述等式的正实数k，t不存在。…………14分
18．解法一：（1）∠PMD为二面角P－MN－D的平面角。…………4分
计算得二面角P－MN－D的大小为120°。…………8分
（2）①若∠CDN＝90°，与题意不符………………10分
②若∠DCN＝90°，可算得
…………12分
③若∠DNC＝90°，可算得
…………15分
解法二：用向量方法
（1）略………………7分
（2）①∠CDN＝90°，………………9分
②若∠DCN＝90°，………………12分
③若∠DNC＝90°，………………15分
19.（考查知识点：概率及分布列）
解:(I)设袋中原有
个白球,由题意知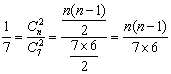
∴(－1)=6得
或
(舍去)即袋中原有3个白球.
(II)由题意,的可能取值为1,2,3,4,5
所以的分布列为:
|
| 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
|
(III)因为甲先取,所以甲只有可能在第1次,第3次和第5次取球,记”甲取到白球”为事件
,则
∵事件
两两互斥，
∴
20．解：设点的坐标
则
……1分
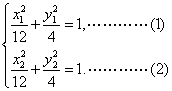…………………………………………………………3分
由（1）－（2）可得
………………………………6分
又MN⊥MQ，
所以
直线QN的方程为
，又直线PT的方程为
……10分
从而得
所以
代入（1）可得
此即为所求的轨迹方程.………………13分
21．解：（1） ∵f ’(x)＝－3x2＋6x＋a …………………………………1’
∴f ’(1)＝3＋a=12,∴a=9 …………………………………3’
（2） f ’(x)＝－3x2＋6x＋9．
令f ‘(x)<0，解得x<－1或x>3， …………………………………5’
所以函数f(x)的单调递减区间为（－∞，－1），（3，＋∞）．………………7’
（3）因为f(－2)＝8＋12－18＋b=2＋b，
f(2)＝－8＋12＋18＋b＝22＋b，
所以f(2)>f(－2)． ……………………………8’
因为在（－1，3）上f ‘(x)>0，
所以f(x)在[－1, 2]上单调递增，又由于f(x)在[－2，－1]上单调递减，
因此f(2)和f(－1)分别是f(x)在区间[－2，2]上的最大值和最小值，
于是有 22＋b＝20，解得 b＝－2． …………………………………10’
故f(x)=－x3＋3x2＋9x－2，因此f(－1)＝1＋3－9－2＝－7，
即函数f(x)在区间[－2，2]上的最小值为－7． ………………………………12’
22（Ⅰ）证法一：因为A、B分别是直线l：
与x轴、y轴的交点，所以A、B的坐标分别是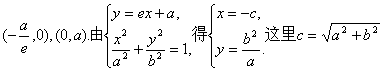
.
所以点M的坐标是（
）. 由
即
证法二：因为A、B分别是直线l：与x轴、y轴的交点，所以A、B的坐标分别是
设M的坐标是
所以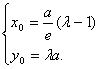
因为点M在椭圆上，所以 
即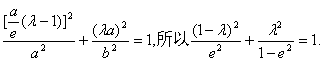
解得
（Ⅱ）当时，
，所以
由△MF1F2的周长为6，得
所以
椭圆方程为
（Ⅲ）解法一：因为PF1⊥l，所以∠PF1F2=90°+∠BAF1为钝角，要使△PF1F2为等腰三角形，必有PF1=F1F2，即
设点F1到l的距离为d，由
得
所以
即当
△PF1F2为等腰三角形.
解法二：因为PF1⊥l，所以∠PF1F2=90°+∠BAF1为钝角，要使△PF1F2为等腰三角形，必有PF1=F1F2，
设点P的坐标是
，
则
由PF1=F1F2得
两边同时除以4a2，化简得
从而
于是
. 即当
时，△PF1F2为等腰三角形.