南昌十六中2005-2006年高三周练卷(7)
2005-11-9
一、选择题(本题每小题5分,共60分)
1.命题甲:![]() ;命题乙:
;命题乙:![]() ,则命题甲是命题乙的
,则命题甲是命题乙的
A.充分非必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要的条件
2.设函数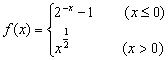 若
若![]() 的取值范围是( )
的取值范围是( )
A.(-1,1) B.(-1,+∞)
C.![]() D.
D.![]()
3.已知函数![]() 的反函数
的反函数![]() ,若
,若![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A.1
B.![]() C.
C.![]() D.
D.![]()
4.若函数![]() 是定义在
是定义在![]() 上的偶函数,在区间
上的偶函数,在区间![]() 上是减函数,且
上是减函数,且![]() ,则使
,则使![]() 的
的![]() 的取值范围为 ( )
的取值范围为 ( )
![]() .
. ![]()
![]() .
. ![]()
![]() .
. ![]()
![]() .
. ![]()
5.已知![]() 在区间
在区间![]() 上递增,则实数
上递增,则实数![]() 的取值范围是( )
的取值范围是( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
6. 已知
{ a![]() }的前n项S
}的前n项S![]() =n
=n![]() - 4n + 1 则∣a
- 4n + 1 则∣a![]() ︱+︱a
︱+︱a![]() ︱+ ……+︱a
︱+ ……+︱a![]() ︱等于
︱等于
A 67 B 65 C 61 D 56
7.在等比数列![]() 中,则
中,则![]() ·
·![]() =6,
=6,![]() ,则
,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
8.函数![]() 的图象为
的图象为![]() ,而
,而![]() 关于直线
关于直线![]() 对称的图象为
对称的图象为![]() ,将
,将![]() 向左平移1个单后得到的图象为
向左平移1个单后得到的图象为![]() ,则
,则![]() 所对应的函数为
所对应的函数为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.设函数![]() 是定义
是定义![]() 在上的且以为3周期的奇函数,若
在上的且以为3周期的奇函数,若![]() ,则
,则
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10若动点![]() 的横坐标
的横坐标![]() 、纵坐标
、纵坐标![]() 使
使![]() 、
、![]() 、
、![]() 成等差数列,则点
成等差数列,则点![]() 的轨迹图形是
的轨迹图形是




11.如果圆![]() 至少覆盖函数
至少覆盖函数![]() 的一个最大点和一个最小点,则正整数
的一个最大点和一个最小点,则正整数![]() 的最小值为
的最小值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.规定记号“![]() ”表示一种运算,即
”表示一种运算,即![]() .若
.若![]() ,则函数
,则函数![]() 的值域是 ( )
的值域是 ( )
A. ![]() B.
B. ![]() C.
C.
![]() D .
D .![]()
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在题中横线上.
13.已知等差数列![]() 的公差
的公差![]() 且
且![]() 成等比数列,则
成等比数列,则![]() 的值为 。
的值为 。
14.在等比数列{an}中,前n项和![]() ,则a12+a22+a32+…+an2等于
。
,则a12+a22+a32+…+an2等于
。
15、已知函数![]() 函数
函数![]() 则
则![]() ;
;
16.函数![]() 是R上的单调函数且对任意的实数都有
是R上的单调函数且对任意的实数都有![]() ,
,![]() 则不等式
则不等式![]() 的解集为__________________________.
的解集为__________________________.
三、解答题:本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤.
17、(本小题满分12分)
已知函数![]() ,
,
(1) 若x∈![]() ,求
,求![]() 的最值。
的最值。
(2) 求解不等式![]() ≤
≤![]() ,
,
18.已知数列![]() 是等差数列,其前项和为
是等差数列,其前项和为![]() 。
。
(1)求数列![]() 的通项公式
的通项公式
(2)设p,q是正整数,且p![]() q,证明
q,证明![]()
19. 袋中有大小相同的5个白球和3个红球,从中任意摸出3个,记摸出白球为-1分,摸出红球为1分。ξ表示摸出3个球后的总分,求ξ的数学期望。
20.数列{an}的首项a1=a≠![]() ,且
,且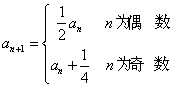 ,
,
记![]() ,n==l,2,3,…·.
,n==l,2,3,…·.
(I)求a2,a3;
(II)判断数列{bn}是否为等比数列,并证明你的结论;
(III)求![]() .
.
21. 已知三棱锥P-ABC中,E、F分别是AC、AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.
(Ⅰ)证明PC⊥平面PAB;
(Ⅱ)求二面角P-AB-C的平面角的余弦值;
(Ⅲ)若点P、A、B、C在一个表面积为12π的球面上,求△ABC的边长.
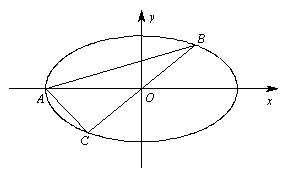
22. 已知椭圆![]() 为常数,且
为常数,且![]() ,向量
,向量![]() ,过点
,过点![]() 且以
且以![]() 为方向向量的直线与椭圆交于点
为方向向量的直线与椭圆交于点![]() ,直线
,直线![]() 交椭圆于点
交椭圆于点![]() (
(![]() 为坐标原点).
为坐标原点).
(Ⅰ) 用![]() 表示
表示![]() 的面积
的面积![]() ;
;
(Ⅱ) 若![]() ,求
,求![]() 的最大值.
的最大值.
 南昌十六中2006届高三数学周考试卷(7) 考试时间:2005-11-09
南昌十六中2006届高三数学周考试卷(7) 考试时间:2005-11-09
![]()
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 得分 | 17 | 18 | 19 | 20 | 21 | 22 | |||
|
|
|
|
|
|
| ||||
一、选择题答题表:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题答题表:
13、 14、
15、 16、
三、解答题(本题17—21小题每题12分,22小题14分,共74分)
17、(本小题满分12分)
18、(本小题满分12分)
19、(本小题满分12分)
20、(本小题满分12分)
21、(本小题满分12分)
22、(本小题满分14分)
参考答案及部分解答
一、选择题(每小题5分,共60分):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| B | D | B | C | B | A | C | B | D | C | B | A |
11.B 提示:因为![]() 为奇函数,图象关于原点对称,所以圆
为奇函数,图象关于原点对称,所以圆![]() 只要覆盖
只要覆盖![]() 的一个最值点即可,令
的一个最值点即可,令![]() ,解得
,解得![]() 距原点最近的一个最大点
距原点最近的一个最大点![]() ,由题意
,由题意![]() 得正整数
得正整数![]() 的最小值为2
的最小值为2
二、填空题(每小题4分,共16分)
13.![]() 14.
14.![]() ; 15.2005; 16.[5,10]
; 15.2005; 16.[5,10]
三、解答题(共74分,按步骤得分)
17.解:(1)∵f(x)= 2![]() cos2x-2sinxcosx-
cos2x-2sinxcosx-![]()
=![]() (cos2x+1)-sin2x-
(cos2x+1)-sin2x-![]()
=2cos(2x+![]() )
)
18.(1)设等差数列![]() 的公差为d, 依题意得
的公差为d, 依题意得
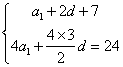 解得
解得![]()
∴![]() 的通项公式为
的通项公式为![]() =
=![]()
(2)证明∵![]() ∴
∴![]()
∵![]()
=![]()
∵![]() ∴
∴![]()
∴![]()
21解法一:
![]()
∴![]() 为所求二面角的平面角.
为所求二面角的平面角.
设AB=a,则![]() ,
,
∴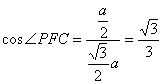 . ……8分
. ……8分
解法二:设P在平面ABC内的射影为O.
![]() ≌
≌![]() ,∴
,∴![]() ≌
≌![]()
得![]() . 于是O是△ABC的中心.
. 于是O是△ABC的中心.
∴![]() 为所求二面角的平面角.
为所求二面角的平面角.
设AB=a,则![]()
∴![]() ……8分
……8分
(Ⅲ)解法一:设PA=x,球半径为R.,
![]()
∴![]() ,
,
![]() ,
,
∴![]() ,得
,得![]() ,
,
∴![]() . ……12分
. ……12分
解法二:延长PO交球面于D,那么PD是球的直径.
连结OA、AD,可知△PAD为直角三角形.
设AB=x,球半径为R.
![]() ,
,
∴![]()
![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() .
.
(22) 解:(Ⅰ) 直线![]() 的方程为
的方程为![]() .………………………………………………2分
.………………………………………………2分
由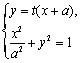 得
得![]() .……………………………………3分
.……………………………………3分
∴![]() 或
或![]() ,即点
,即点![]() 的纵坐标为
的纵坐标为![]() .……………………4分
.……………………4分
∵点![]() 与点
与点![]() 关于原点
关于原点![]() 对称,
对称,
∴![]() .……………………6分
.……………………6分
(Ⅱ) 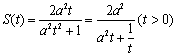 .
.
当![]() 时,
时,![]() ,
,![]() ,
,
当且仅当![]() 时,
时,![]() .…………………………………………………9分
.…………………………………………………9分
当![]() 时,可证
时,可证![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,
,
∴![]() 在
在![]() 上单调递增.
上单调递增.
∴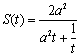 在
在![]() 上单调递减.
上单调递减.
∴当![]() 时,
时,![]() .………………………………………………13分
.………………………………………………13分
综上可得,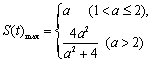 .………………………………………14分
.………………………………………14分