汉寿三中2007届高三第二次月考数学试卷（理科）
时量：120分钟 满分：150分
姓名： 班次： 总分：
一、填空题（每小题5分，共50分）
1. 已知全集Ｕ＝｛a,b,c,d,e,｝，集合A＝｛b,c｝,CUB={c,d},则
（CUA）
B等于（ ）
A．｛a,e｝ B。｛c,b,d｝ C。｛a.c.e｝ D 。｛e｝
2．已知集合M={x
,x、y
}，N={y
x、y},则MN等于（ ）
Ａ.
Ｂ.
R Ｃ. M Ｄ. N
3. 对于
，给出下列四个不等式：
①
；②
；
③
； ④
。
其中成立的是（ ）
A ①，③ B ①，④ C ②，③ D ②，④
4．下列命题中，p是q的充要条件的是（ ）
A．p:a>-1, q: 二元一次方程组
有唯一解
B．p:两条对角线互相垂直平分， q: 四边形是正方形
C．p:x+1>2x+1, q:
D. a,b,c为实数， p: ac2>bc2, q:a+c>b+c
5.甲、乙、丙、丁四位同学对参加29届奥运会的中国男110米栏的4个运动员A、B、C、D作赛前预猜：
甲说：“C或D将得冠军。” 乙说：“D将得冠军.”
丙说：“得冠军得应是C.” 丁说：“A和C不可能得冠军。”
赛后证明，以上四位同学得预猜中只有两句是对的，
那么冠军是谁（ ）
A. A B. B C. C D. D
6、 设集合P＝｛a，b，2｝，Q＝｛2a，2，b2｝，且P＝Q，则a与b的值为（ ）
A．a＝0，b＝1 B．a＝
，b ＝
C．a＝0，b＝1或a＝，b ＝ D．以上均不对
7.函数
的图象是曲线C，则曲线C与直线
（ ）
A一定有一个交点 B 至少有一个交点 C 最多有一个交点 D 有无数个交点。
8.当0≤x≤1时，函数y=ax+a－1的值有正值也有负值，则实数a的取值范围是（ ）
A.a<
B.a>1 C.a<或a>1 D.<a<1
9、已知：
则
（ ）
A 2 B 4 C 6 D 8
10、已知
是奇函数，且在
上是增函数，若
，则不等式
的解集是（ ）
A
B
C
D
二、填空（每小题4分，共20分）
11、已知p：2x－3＜1，q：x（x－3）＜0，则p是q的 条件
12、若集合A
B, AC, B=｛0,1,2,3,4,7,8｝, C=｛0,3,4,7,8｝, 则A的个数为 .
13、设集合
}则集合M
N中元素的个数为
.
14.函数y=
+log
x的值域是 。
15、函数的定义域是
，已知
是奇函数，当
时，
，则当
时，的递增区间是 。
三、解答题：（6个小题，共80分）
16、（12分）已知集合P={xx2－5x+4≤0},Q={xx2－2bx+b+2≤0}满足P
Q，求实数b的取值范围。
17．（12分）二次函数f(x)满足f (x＋1)－f (x)＝2x且f (0)＝1．
⑴求f (x)的解析式；⑵在区间[－1，1]上，y＝f (x)的图象恒在y＝2x＋m的图象上方，试确定实数m的范围．
18．（14分）已知集合A＝
，B＝
．
⑴当a＝2时，求AB； ⑵求使BA的实数a的取值范围．
19．（14分）已知命题
：方程
在[－1，1]上有解；命题
：只有一个实数
满足不等式
，若命题“p或q”是假命题，求实数a的取值范围．
20、（14分）设集合A={x4x－2x+2+a=0,x∈R}。
（1）若A中仅有一个元素，求实数a的取值集合B；
（2）若对于任意a∈B，不等式x2－6x<a(x－2)恒成立，求x的取值范围。
21、（14分）设a为实数，记函数
的最大值为g(a)。
（Ⅰ）设t＝
，求t的取值范围，并把f(x)表示为t的函数m(t)；
（Ⅱ）求g(a)；
（Ⅲ）试求满足
的所有实数a。
参考答案
1~10 ADBCC CCDBB
11~15
11.充分不必要 12.32个 13.2 14 
15. 
16. 解 显然P={x1≤x≤4}，记f(x)=x2－2bx+b+2
若Q为空集，则由Δ<0得：4b2－4(b+2)<0 ∴－1<b<2。
若Q不是空集，则应满足
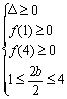即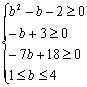
解之得：2≤b≤
综上得：－1<b≤
17. 解： (1)设f（x）＝ax2＋bx＋c，由f（0）＝1得c＝1，故f（x）＝ax2＋bx＋1．
∵f(x＋1)－f(x)＝2x，∴a(x＋1)2＋b(x＋1)＋1－(ax2＋bx＋1)＝2x．
即2ax＋a＋b＝2x，所以
，∴f(x)＝x2－x＋1．
(2)由题意得x2－x＋1>2x＋m在[－1，1]上恒成立．即x2－3x＋1－m>0在[－1，1]上恒成立．
设g(x)＝ x2－3x＋1－m，其图象的对称轴为直线x＝，所以g(x) 在[－1，1]上递减．
故只需g(1)>0，即12－3×1＋1－m>0，解得m<－1．
18. 解：（1）当a＝2时，A＝（2，7），B＝（4，5）∴ AB＝（4，5）．
（2）∵ B＝（2a，a2＋1），
当a＜
时，A＝（3a＋1，2）
要使BA，必须
，此时a＝－1；
当a＝时，A＝，使BA的a不存在；
当a＞时，A＝（2，3a＋1）
要使BA，必须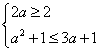
，此时1≤a≤3．
综上可知，使BA的实数a的取值范围为[1，3]∪{－1}
19.
20.
解：（1)令2x=t(t>0)，设f(t)=t2－4t+a,由f(t)=0在（0，+∞）上仅有一根或两相等实根、有
①f(t)=0有两等根时，△=0
16－4 a =0a=4.
验证:t2－4t+4=0t=2
(0,+∞)这时x=1.
②f(t)=0有一正根和一负根时，f(0)<0a<0.
③若f(0)=0，则a=0，此时4x－2·2x=0
，（舍去），或2x=4,∴x=2，此时A中只有一个元素。
∴实数a的取值集合为B={ a≤0或a=4}。
(2)要使原不等式对任意a(－∞,0
{4}恒成立，即g(a)=（x－2）a－(x2－6x)>0恒成立。
只须
5－
<x≤2.
21. （I）∵
，
∴要使
有意义，必须
且
，即
∵
，且
……① ∴的取值范围是
。
由①得：
，∴
，
。
（II）由题意知
即为函数
，的最大值，
∵直线
是抛物线的对称轴，∴可分以下几种情况进行讨论：
（1）当
时，函数
，的图象是开口向上的抛物线的一段，
由
知在上单调递增，故
；
（2）当
时，
，，有=2；
（3）当
时，，函数，的图象是开口向下的抛物线的一段，
若
即
时，
，
若
即
时，
，
若
即
时，。
综上所述，有=
。
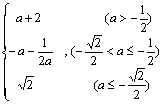（III）当
时，
；
当
时，
，
，∴
，
，故当
时，
；
当时，
，由
知：
，故
；
当时，
，故
或
，从而有
或
，
要使，必须有
，
，即
，
此时，。
综上所述，满足的所有实数a为：或。