2005学年杭州二中高三年级第四次月考
数学试卷 （理科） 06.1.13
命题：杨永华 校对：徐存旭
一．选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.
（1）设全集U=R，集合M={x x>1}，P={x x2>1}，则下列关系中正确的是 （ ）
（A）M＝P （B）P
M （C）MP （D）
（2）复数
等于 （ ）
（A）
（B）
（C）
（D）
（3）若“p或q”成立的充分条件是“┐r”，则推理：①p或q
┐r；②┐rp；③r ┐(p或q)
；④┐p且┐qr ，正确的个数为
( )
（A）0 （B）1 （C） 2 （D）3
（4）已知
是定义在实数集R上的函数，它的反函数为
，若
与
互为反函数，且
（
为非零常数），则
的值为 （ ）
（A）
（B）
（C）0
（D）
（5）市区某公共汽车站有10个候车位（成一排），现有4名乘客随便坐在某个座位上候车，则恰好有5个连续空座位的候车方式的概率为（ ）
（A）
（B）
（C）
（D）
（6）函数
的图象与直线
的位置关系是 ( )
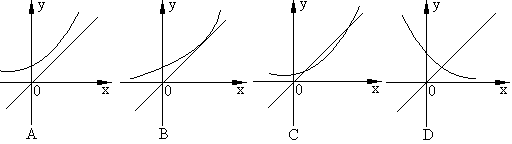（7）已知
是等比数列，公比为
，设
（其中
），且
（其中），如果数列
有极限，则公比的取值范围是
（ ）
（A）
且
（B）
且
（C）
且
（D）
且
（8）一同学在电脑中按
编制一个程序生成若干个实心圆（
表示第
次生成的实心圆的个数）并在每次生成后插入一个空心圆，当某次生成的实心圆个数达到2016时终止，则此时空心圆个数为
（ ）
（A）445 （B）64 （C）63 （D）62
（9）当
时，函数
的最小值为
( )
（A）2 （B）
（C）4 （D）
（10）已知向量
，则
的取值范围是
（ ）
（A）
（B）
（C）
（D）
二、填空题：本大题共4小题，每小题4分，共16分.
（11）在
的展开式中常数项是第 项.
（12）
.
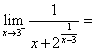（13）某次高三的两个班级数学单元测验服从正态分布N
，巳知第100名的成绩为60分，问笫20名的成绩为 . （参考数据：
）
（14）有9个乒乓球，其中2只是相同的，均为红色，有4只是白色的，也是相同的，剩下3只球均不相同，颜色为黄，兰，黑.某人从这9个球中至少拿一只，有多少种拿法 .
2005学年杭州二中高三年级第四次月考
数学（理科）答题卷
第Ⅰ卷（选择题 共50分）
一．选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.把答案填写在对应方格内.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
第Ⅱ卷（非选择题 共100分）
注意事项：
1．第Ⅱ卷共4页，用钢笔或圆珠笔直接答在答题卷中.
2．答卷前将密封线内的项目填写清楚.
二．填空题：本大题共4小题，每小题4分，共16分．把答案填在答卷中的横线上.
（11） （12）
（13） （14）
三．解答题：本大题共6小题，每小题14分，共84分．解答应写出文字说明，证明过程或演算步骤.
（15）（本小题满分14分）
已知集合
.
（Ⅰ）当
时，求
；
（Ⅱ）求使
的实数a的取值范围.
（16）（本小题满分14分）
在△ABC中，已知
，
（Ⅰ）求
；
（Ⅱ）设∠BAC=
，且已知
，求
.
（17）（本小题满分14分）
已知函数
，
在
处取得极小值
.
（Ⅰ）求函数的单调区间；
（Ⅱ）若
对
恒成立，求实数m的取值范围.
（18）（本小题满分14分）
数列{}满足递推式
其中
，
（Ⅰ）求
； （Ⅱ）若存在一个实数
，使得
为等差数列，求值;
（Ⅲ）求数列{}的前n项之和.
（19）（本小题满分14分） 某医院为了提高服务质量，进行了下面的调查发现：当还未开始挂号时，有N个人已经在排队等候挂号．开始挂号后排队的人数平均每分钟增加M人．假定挂号的速度是每窗口每分钟K个人，当开放一个窗口时，40分钟后恰好不会出现排队现象；若同时开放两个窗口时，则15分钟后恰好不会出现排队现象．根据以上信息，请你解决以下问题：
（Ⅰ）若要求8分钟后不出现排队现象，则至少需要同时开放几个窗口？
（Ⅱ）若医院做出承诺，开始挂号后每人等待的时间不超过25分钟，问：若
＝60，当只开放一个窗口时，能否实现做出的承诺？
（20）（本小题满分14分）
设关于x的方程
的两根为
函数
（Ⅰ）求
的值；
（Ⅱ）证明：在[
上是增函数；
（Ⅲ）对任意正数
,求证：
.
参考答案
一、选择题：每小题5分，共60分
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | B | B | C | A | C | A | D | C | D |
二、填空题，每小题4分，共16分
11． 7
12．
13．79.6 14．119
三、解答题（共74分）
15．解：（1）当a=2时，A=（2，7），B=（4，5）∴A∩B=（4，5）………………4分
（2）∵B=（2a,a2+1），当a<
时，A=（3a+1，2）………………………………6分
要使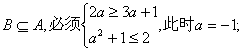
……………………………… 8分
当a=时，A=φ，使B
A的a不存在；………………………………… 10分
当a>时，A=（2，3a+1）
要使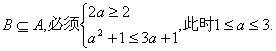
…………………………12分
综上可知，使BA的实数a的取值范围为[1，3]∪{－1}……………… 14分
16．（本小题满分14分）
（1）
，
(2)
17. （1）
，由
由
则
，
（2）由
则
要使对恒成立，只要
就可以了，
即 得
所以实数m的取值范围是
18．解：（1）由
同理求得a2=23, a1=5
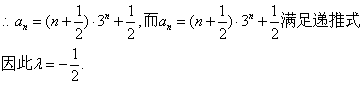
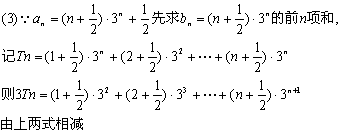
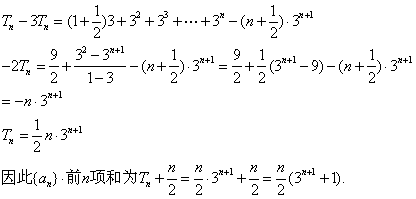
19．解：（Ⅰ）设要同时开放x个窗口才能满足要求，
则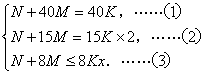 
由（1）、（2）得
代入（3）得60M＋8M ≤8×2.5Mx，解得x≥3.4．
故至少同时开放4 个窗口才能满足要求．
（Ⅱ）N＝60时，K＝2.5，M＝1，设第n个人的等待时间为
．
当n≤60时，第n个人的等待时间为他前面的n－1个人挂号完用去的时间；
当n＞60时，第n个人的等待时间为他前面的n－1个人挂号．
用去的时间减去他在开始挂号后到来挂号用去的时间 ，即
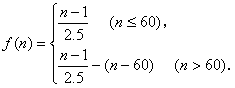
当n≤60时，则当n＝60时，取最大值为23.6分钟．
当n＞60时，则当n＝61时，取最大值为23分钟．
故等待时间最长为23.6分钟，说明能够实现承诺．
20．解析：（1）由根与系数的关系得，
同法得f(
(2).证明：
f/(x)=
而当x
时，
2x2-tx-2=2(x-
故当x时, f/(x)≥0,
函数f(x)在[上是增函数。
（3）。证明：
, 同理
.
又f(
两式相加得:
即
而由（1），f(
且f(
,
.