培优练习（1）2004－02－24
一、选择题：
1、已知函数
的图象过（1，0），则
的反函数的图象一定过点（ ）
A．（1，2） B．（2，1） C．（0，2） D．（2，0）
2、从P点引三条射线PA，PB，PC，每两条射线夹角为60°，则平面PAB和平面PBC所成二面角正弦值为 （ ）
A．
B．
C．
D．
3、已知x，y满足不等式组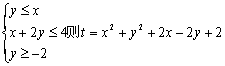
的最小值为 （ ）
A．
B．2 C．3 D．
|
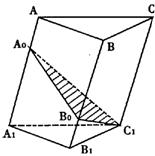
AA1，BB1上的点，且知BB0:B0B1=3:2，过A0，B0，C1
的截面将三棱柱分成上下两个部分体积之比为2:1，则
AA0:A0A1= （ ）
A．2:3 B．4:3
C．3:2 D．1:1
二、填空题：
5、
.
6、某气象站天气预报准确率是80%，5次预报中至少有4次准确的概率是
（精确到0.01）.
7、设a，b都是正实数，且2a+b=1，设
则当a=______且b=_______时，T的最大值为_______。
8、如图，矩形ABCD中，
，AD=1，在DC上截取DE=1，将△ADE沿AE翻折到
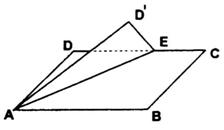D′点，当D′在平面ABC上的射影落在AE上时，四棱锥D′—ABCE的体积是________；当D′在平面ABC上的射影落在AC上时，二面角D′—AE—B的平面角的余弦值是_________。
三、解答题：（过程要完整、表述要规范）
9、（本小题满分12分）
是否存在常数c，使得不等式
对任意正实数x、y恒成立？证明你的结论．
10、（本小题满分12分）
甲乙两人独立解某一道数学题，已知该题被甲独立解出的概率为0.6，被甲或乙解出的概率为0.92.
（1）求该题被乙独立解出的概率；（2）求解出该题的人数
的数学期望和方差.
11、（本小题满分14分）
已知
（Ⅰ）若
能表示成一个奇函数
和一个偶函数
的和，求和
的解析式；
（Ⅱ）若和在区间
上都是减函数，求a的取值范
（Ⅲ）在（Ⅱ）的条件下，比较
的大小．
12、（本小题满分12分）
已知定义域为[0，1]的函数f (x)同时满足：
（1）对于任意x∈[0，1]，总有f (x)≥0；
（2）f (1) =1；
（3）若
，
，
，则有
。
（Ⅰ）试求f(0)的值；
（Ⅱ）试求函数f(x)的最大值；
（Ⅲ）试证明：满足上述条件的函数f(x)对一切实数x，都有f(x)≤2x 。
13、（本小题满分16分）
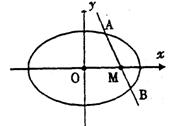
在直角坐标平面内，已知两点A（-2，0）及B（2，0），动点Q到点A的距离为6，线段BQ的垂直平分线交AQ于点P。
（Ⅰ）证明PA+PB为常数，并写出点P的轨迹T的方程；
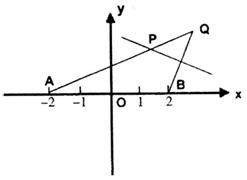（Ⅱ）过点B的直线l与曲线T相交于M、N两点，线段MN的中点R与点S（-1，0）的连线的纵截距为t，试求t 的取值范围。
14、（本小题满分14分）
（文科）已知椭圆C的中心在原点，焦点在x轴上，一条经过点
且方向向量为
的直线l通过椭圆C的右焦点F，且交椭圆C于A、B两点，又
（1）求直线l的方程； （2）求椭圆C的方程.
（理科）已知椭圆C的中心在原点，焦点在x轴上，一条经过点（3，－
）且方向向量为的直线l交椭圆C于A、B两点，交x轴于M点，又
.
（1）求直线l方程； （2）求椭圆C长轴长取值的范围.
培优练习（1）答案
一、选择题：AABA
二、填空题：5．
6．0.74; 7．
；
；
； 8．
；
三、9、（本题满分12分）
解： 当
时，由已知不等式得
……3分
下面分两部分给出证明：
⑴先证
，
此不等式
，此式显然成立；
……7分
⑵再证
，
此不等式
，此式显然成立．
……10分
综上可知，存在常数
，是对任意的整数x、y，题中的不等式成立．12分
10、（本题满分12分）
解：（1）记甲、乙分别解出此题的事件记为A、B.
设甲独立解出此题的概率为P1，乙为P2. （2分）
则P（A）=P1=0.6, P(B)=P2
|
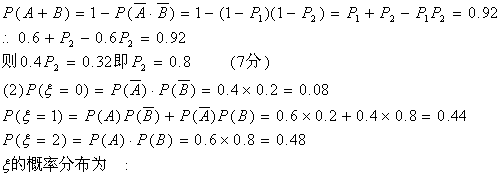
| 0 | 1 | 2 |
| P | 0.08 | 0.44 | 0.48 |
11、（本题满分14分）
解：（Ⅰ）设
①，其中是奇函数，是偶函数，
则有 
②
联立①，②可得
，
（直接给出这两个函数也给分）…3分
（Ⅱ）函数 当且仅当 
，即
时才是减函数，
∴
又
∴的递减区间是 
……5分
由已知得
∴ 
解得
∴
取值范围是
……8分
（Ⅲ）
在
上为增函数 ……10分
∴
∴
即
. ……14分
12、（本题满分12分）
解：（Ⅰ）令
，
依条件（3）可得f(0+0) ≥f(0)+f(0)，即f(0) ≤0。
又由条件（1）得f(0) ≥0，则f(0)=0…………………… 3分
（Ⅱ）任取
，可知
则
…………… 5分
即
，故
于是当0≤x≤1时，有f(x)≤f(1)=1
因此，当x=1时，f(x)有最大值为1，………………… 7分
（Ⅲ）证明：研究①当
时，f(x) ≤1<2x
②当
时，
首先，f(2x) ≥f(x)+f(x)=2f(x)，∴
………………9分
显然，当
时，
成立。
假设当
时，有
成立，其中k＝1，2，…
那么当
时，
可知对于
，总有
，其中n=1，2，…
而对于任意，存在正整数n，使得
，
此时
…………………
…11分
③当x=0时，f(0)=0≤2x………… ……12分
综上可知，满足条件的函数f(x)，对x∈[0，1]，总有f(x) ≤2x成立。
13、（本题满分16分）
解：（Ⅰ）连结PB。∵线段BQ的垂直平分线与AQ交于点P，
∴PB=PQ，又AQ=6，
∴PA+PB=PA+PQ=AQ=6（常数）。 …2分
又PA+PB>AB，从而P点的轨迹T是中心在原点，以A、B为两个焦点，长轴在x轴上的椭圆，其中，2a=6，2c=4，
∴椭圆方程为
…6分
（Ⅱ）当直线l与x轴垂直时，MN的中点为R（2，0）
直线RS的纵截距t =0 …7分
当直线l与x轴不垂直时，设其斜率为k，
点
、
、
。
由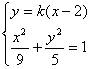
，消去y整理得：
…9分
∴
，
则
直线RS的方程为
。
令x=0，可得直线RS的纵截距
。
如果k=0，则t=0；
如果k≠0，则
。
∵
当且仅当
时，等号成立。
…14分
∴
或
综上可知，所求t的取值范围是
。
…16分
14、（本题满分12分）
（文）解：（1）直线l过点（3，－）且方向向量为
……………………………………（4分）
（2）设直线
，
由
……………………………………………………（7分）
将
，
整理得
|
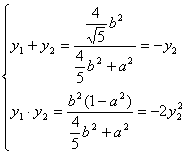（9分）
由①2/②知 
……………………………………（12分）
又
因此所求椭圆方程为：
…（14分）
（理）解：（1）直线l过点（3，－）且方向向量为
|
化简为：
…………（4分）
（2）设直线
交于两点A（x1,y1），B（x2,y2），和x轴交于M（1，0）
由
………………………………………………（7分）
将
…………………………………………①
|
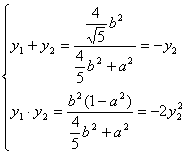
由②2/③ 知：32b2=（4b2+5a2）（a2－1）…………………………………………（10分）
化为
………………………………………………④
对方程①求判别式，且由△>0
即
化简为：
………………………………………………⑤ 12分
由④式代入⑤可知：
又椭圆的焦点在x轴上，
则
由④知：
因此所求椭圆长轴长2a范围为（
14分