二00六年普通高等学校招生统一考试
数学仿真模拟试卷（一）
第Ⅰ卷（选择题，共60分）
一、选择题：本大题共12个小题，每小题5分，共60分．
1．已知直线x=k(k>0)和圆(x－1)2+y2=4相切，那么k的值是 （ ）
A．5 B．4 C．3 D．2
2．函数
的图象的一条对称轴方程是 （ ）
A．x=
B．x=
C．x=
D．x=
3．向量
=（1，2），
=(x,1), 
=+2,
∥
，则x的值是 （ ）
A．
B．
C．
D．
4．已知x、y满足约束条件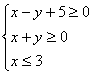
，则z=x+2y的最小值为（ ）
A．-3 B．3 C．-5 D．5
5．椭圆5x2+ky2=5的一个焦点是（0，2），则k等于 （ ）
A、－1
B、1
C、
D、
6．不等式
的解集是
（ ）
A、{x0≤x<1} B、{xx<0且x≠－1}
C、{x－1<x<1} D、{xx<1且x≠－1}
7．
则
的值为 （ ）
A、0
B、-1
C、1
D、
8．已知m，
是异面直线，给出下列四个命题：①必存在平面
，过m且与都平行；②必存在平面 
，过m且与垂直；③必存在平面r，与m，都垂直；④必存在平面w, 与m，的距离都相等。其中正确的结论是 （ ）
A．①② B．①③ C．②③ D．①④
9．过圆
内一点（5，3）有k条长度成等差数列的弦，且最小弦长为首项
，最大弦长为末项
，若公差d满足d
,则k的取值不可能是（ ）
A.4 B.5 C.6 7
10.关于
的函数
有与
轴垂直的切线，则
的关系是（ ）A.
B.
C.
D.
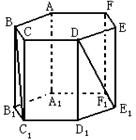11．正六棱柱ABCDEF—A1B1C1D1E1F1的底面边长为1，侧棱长为
，则这个棱柱的侧面对角线E1D与BC1所成的角是
（ ）
A、900 B、600 C、450 D、300
12．设函数f(x)是定义在R上的以3为周期的奇函数，若f(x)>1，f(2)= 
，则（ ）
A. a<
B. a<
C. a>
D. －1<a<
二、填空题 (本大题共4小题，每小题4分，共16分。把答案填在题中横线上)
13．某校有高中生1200人，初中生900人，老师120人，现用分层抽样的方法从所有师生中抽取一个容量为N的样本；已知从初中生中抽取人数为60人，那么N=__________。
14.若
与
的展开式中各项系数之和分别为，
，则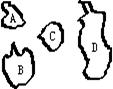
= .
15．如图，A，B，C，D为海上的四个小岛，要建三座桥，将这四个小岛连接起来，则不同的建桥方案共有__________.(用数字作答)
16．直线
和圆
交于A和B，以OX为始边，OA、OB为终边的角分别为、，则sin(+)的值为 .
第二卷
填空题答题栏
13、 14、 15、 16、
三、解答题：本大题共6小题，共74分.解答写出文字说明，证明过程或演算步骤
17．(本题满分12分)已知f（x）=4msinx — cos2x (x∈R)，若f（x）的最大值为3，求实数m的值。
18．(本题满分12分) 已知数列{an}的各项均为正数，且前n项和Sn满足
．若a2、a4、a9 成等比数列，求数列{an}的通项公式．
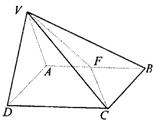
19．（本题满分12分）如图，平面VAD⊥平面ABCD，△VAD是等边三角形，ABCD是矩形，AB∶AD＝∶1，F是AB的中点．
（1）求VC与平面ABCD所成的角；
（2）求二面角V-FC-B的度数；
（3）当V到平面ABCD的距离是3时，求B到平面VFC的距离．
20．（本小题满分12分）
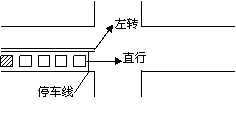如图，一辆车要通过某十字路口，直行时前方
刚好由绿灯转为红灯，该车前面已有4辆车依次在
同一车道上排队等候（该车道只可以直行或左转行
驶）。已知每辆车直行的概率是，左转行驶的概率
是
，该路口红绿灯转换间隔均为1分钟。假设该车道上一辆直行的车驶出停车线需要10秒，一辆左转的车驶出停车线需要20秒，求：
（1）前4辆恰有2辆左转行驶的概率；
（2）该车在第一次绿灯亮起时的1分钟内通过该路口的概率；（汽车驶出停车线就算通过路口）
21．（本题满分12分）已知函数f(x)=－x3＋3x2＋ax＋b在x＝(1，f(1))处的切线与直线12x－y－1＝0平行．
（1）求实数a的值；
（2）求f(x)的单调递减区间；
（3）若f(x)在区间[－2，2]上的最大值为20，求它在该区间上的最小值．
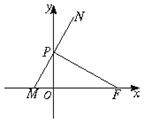22．（本题满分14分）如图，点F（a，0）（a>0），点P在y轴上运动，M在x轴上，N为动点，且
0.
（1）求点N的轨迹C的方程；
（2）过点F（a，0）的直线l（不与x轴垂直）与曲线C交于A、B两点，设点K（－a，0），
与
的夹角为θ，
求证：0<θ<
.
数学仿真模拟试卷（一）答案
一、CBAAB DCDAA BD
二、148 
16 
三、17、本小题主要考查三角函数的基础知识，以及换元配方法，分类讨论思想方法和运算能力，.
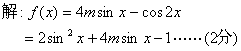
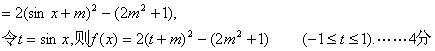
①
……7分
②
综上,
……12分
18、解 ∵ 对任意nÎN*，有 ， (1)
∴ 当n=1时，有 
，
解得 a=1 或a1 = 2． ……… 3分
当n≥2时，有 
．
(2)
于是，由 (1)－(2) 整理可得 (an + an－1)(an－an－1－3)=0．
因为{an}的各项均为正数，所以 an－an－1 = 3． …………… 8分
当a1 = 1时，an =1+3(n－1)=3n－2，此时a42=a2a9成立．
当a1 = 2时，an =2+3(n－1)=3n－1，此时a42=a2a9不成立，故a1=2舍去．
所以an=3n－2． ……………… 12分
19、解析：取AD的中点G，连结VG，CG．
（1）∵ △ADV为正三角形，∴ VG⊥AD．
又平面VAD⊥平面ABCD．AD为交线，
∴ VG⊥平面ABCD，则∠VCG为CV与平面ABCD所成的角．
设AD＝a，则
，
．
在Rt△GDC中，
．
在Rt△VGC中，
．
∴ 
．
即VC与平面ABCD成30°．
（2）连结GF，则
．
而 
．
在△GFC中，
． ∴ GF⊥FC．
连结VF，由VG⊥平面ABCD知VF⊥FC，则∠VFG即为二面角V-FC-D的平面角．
在Rt△VFG中，
．
∴ ∠VFG＝45°． 二面角V-FC-B的度数为135°．
（3）设B到平面VFC的距离为h，当V到平面ABCD的距离是3时，即VG＝3．
此时
，
，
，
．
∴ 
，
．
∵ 
，
∴ 
．
∴ 
．
∴ 
即B到面VCF的距离为．
20、解：（1）前4辆恰有2辆左转行驶的概率
（2）该车在第一次绿灯亮起时的1分钟内通过该路口的概率
答：前4辆恰有2辆左转行驶的概率是
；该车在第一次绿灯亮起时的1分钟内通过该路口的概率是
21、解：（1） ∵f ’(x)＝－3x2＋6x＋a …………………………………1’
∴f ’(1)＝3＋a=12,∴a=9 …………………………………3’
（2） f ’(x)＝－3x2＋6x＋9．
令f ‘(x)<0，解得x<－1或x>3， …………………………………5’
所以函数f(x)的单调递减区间为（－∞，－1），（3，＋∞）．………………7’
（3）因为f(－2)＝8＋12－18＋b=2＋b，
f(2)＝－8＋12＋18＋b＝22＋b，
所以f(2)>f(－2)． ……………………………8’
因为在（－1，3）上f ‘(x)>0，
所以f(x)在[－1, 2]上单调递增，又由于f(x)在[－2，－1]上单调递减，
因此f(2)和f(－1)分别是f(x)在区间[－2，2]上的最大值和最小值，
于是有 22＋b＝20，解得 b＝－2． …………………………………10’
故f(x)=－x3＋3x2＋9x－2，因此f(－1)＝1＋3－9－2＝－7，
即函数f(x)在区间[－2，2]上的最小值为－7． ………………………………12’
22、（1）（方法一）设N（x，y），∵
=0，即P是MN的中点，
∴M（－x，0），P（0，
）， ∵
=0，∴PM⊥PF，
∴
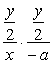=－1， ∴y2=4ax即为所求.
（方法二）设N（x，y），M（x0，0），P（0，y0）
则
由
·
=0，得ax0+y02=0， ①
由
+=0，得（x+x0，y－2y0）=0，
即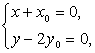
∴
代入①得，y2=4ax即为所求.
（2）设l的方程为y=k（x－a），
由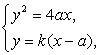
消去x，得y2－
y－4a2=0，
设A（x1，y1），B（x2，y2），则y1y2=－4a2，
=（x1+a，y1），=（x2+a，y2），
·=（x1+a）（x2+a）+y1y2=x1x2+a（x1+x2）+a2+y1y2
=
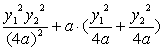+a2－4a2 =
（y12+y22）－2a2>（2y1y2）－2a2
=
×4a2－2a2=0， ∴cosθ=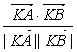
>0， ∴0<θ<.