湖北省安陆一中高三数学易错题重组集锦(二)
一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1、空间四边形ABCD中,AB=CD,且AB、CD成60度角,E、F是AD、BC的中点,则EF与AB所成的角等于 ( )
A.30![]() B.60
B.60![]() C.90
C.90![]() D.以上都不对
D.以上都不对
2、已知lg(x+y)=lgx+lgy,若![]() =4x+y,则
=4x+y,则![]() 的最小值是 ( )
的最小值是 ( )
A. 4 B. 6 C. 8 D.9
3、不等式![]() 的解集为
的解集为![]() ,则k的取值范围是 ( )
,则k的取值范围是 ( )
A. (![]() ,
,![]() ]
B.[0,
]
B.[0, ![]() ] C. (
] C. (![]() ,+
,+![]() ) D. (
) D. (![]() ,0)
,0)![]() (
(![]() , +
, +![]() )
)
4、设A、B,C,D是半径为2的球面上的四点,满足![]() =
=![]() =0,则
=0,则![]() 的最小值为 ( )
的最小值为 ( )
A.2 B. 4 C. 8 D. 16
5、(2x+y-z)6的展开式中,x3y2z这一项的系数为 ( )
A.480 B. 160 C. -480 D.—160
6、已知f(x)=ax+b( 0![]() x
x![]() 1),则a+2b>0是f(x)>0在[0,1]上恒成立的 ( )
1),则a+2b>0是f(x)>0在[0,1]上恒成立的 ( )
A.充分不必要条件 B.必要不充分条件
C. 充要条件 D.既非充分又非必要条件
7、函数y=f(x)与y=1![]() 的图象关于直线
(
)对称
的图象关于直线
(
)对称
A.y=x-1 B.y=x+1 C.y=-x-1 D.y=-x+1
 8、函数y=x(x-2)在[a,b]上的值域为[-1,3],则以a为横坐标,b为纵坐标所成的点(a,b)的轨迹为下图中的 ( )
8、函数y=x(x-2)在[a,b]上的值域为[-1,3],则以a为横坐标,b为纵坐标所成的点(a,b)的轨迹为下图中的 ( )
A.点D(1,3), B(-1,1)
B.线段AB,CD
C.线段AD,BC
D.线段AB,AD
9、考虑一元二次方程x2+mx+n=0,其中m,n的取值分别等于将一枚骰子连掷两次先后出现的点数,则方程有实根的概率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10、已知直线ax+by-1=0 (a,b不全为0)与圆x2+y2=50有公共点,且公共点的横坐标、纵坐标均为整数,那么这样的直线有 ( )
A.66条 B.72条 C.74条 D.78条
二、填空题:(本大题共5小题,每小题5分,共25分.将正确答案填在答题卷上对应题号的横线上.)
11、函数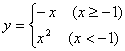 的反函数为
.
的反函数为
.
12、(1)函数y=2x-3+![]() 的值域为
;
的值域为
;
(2)函数y=sin2x-3sinx+4的值域为 .
13、在数列{an}中,已知a1=1,a2=![]() ,且
,且![]()
![]() ,则这个数列的通项公式为
,则这个数列的通项公式为
14、已知实数x,y满足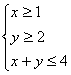 ,则
,则![]() 的取值范围是
的取值范围是
15、函数f(x)=Asin(![]() ) (A>0,
) (A>0,![]() >0)的部分
>0)的部分
图象如图所示,则f(1)+f(2)+f(3)+…+f(11) =
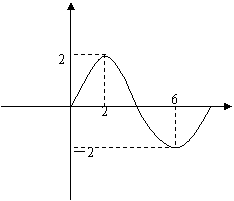 |
湖北省安陆一中高三数学易错题重组集锦(二)答题卡
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题:
11、 12、 ,
13 、 14、
15、
三、解答题:本大题共6小题,满分74分.解答应写出文字说明,证明过程或演算步骤.
16、已知圆内接四边形ABCD的边长分别为AB=2,BC=6,CD=DA=4,求四边形ABCD的面积.
17、已知数列{an}中,![]() (
(![]() )
)
(1)求证:数列{![]() }为等差数列;(2)求通项
}为等差数列;(2)求通项![]() ;(3)求数列
;(3)求数列![]() 的前n项和
的前n项和![]()
18、一个口袋中装有大小相同的2个白球和3个黑球,
(1)从中摸出两个球,求两球恰好颜色不同的概率;
(2)从中摸出一个球,放回后再摸一个球,求两个球恰好颜色不同的概率
19、如图:M,N,P分别是正方体ABCD—A1B1C1D1的棱AB、BC、DD1上的点,
(1)若![]() ,求证:无论点P在DD1上如何移动,总有BP
,求证:无论点P在DD1上如何移动,总有BP![]() MN
MN
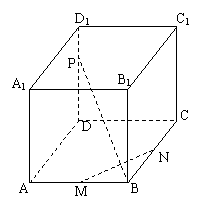 (2)若
(2)若![]() ,且PB
,且PB![]() 面B1MN,求二面角M—B1N—B的大小.
面B1MN,求二面角M—B1N—B的大小.
20、已知三次函数![]() 的导数
的导数![]() 满足
满足![]() ,
,![]() ,
,![]() ,
,
(1)求![]() 的表达式;(2)若对任意
的表达式;(2)若对任意![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范围
的取值范围
21、椭圆E的中心在原点,焦点在x轴上,其离心率e=![]() ,过点C(-1,0)的直线l与椭圆E相交与点A,B,且C分有向线段
,过点C(-1,0)的直线l与椭圆E相交与点A,B,且C分有向线段![]() 的比为2.
的比为2.
(1)用直线l的斜率k(k![]() 0)表示
0)表示![]() 的面积;
的面积;
(2)当![]() 的面积最大时,求椭圆E的方程.
的面积最大时,求椭圆E的方程.
湖北省安陆一中高三数学易错题重组集锦(二)参考答案
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | D | C | C | C | B | D | D | A | B |
二、填空题:
11 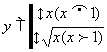 12 (-
12 (-![]() ,4] , [2,8]
,4] , [2,8]
13 ![]() 14
[2,4]
14
[2,4]
15 ![]()
三、解答题:本大题共6小题,满分74分.解答应写出文字说明,证明过程或演算步骤.
16、8![]()
17、(1)略; (2)![]() ; (3)
; (3)![]()
18、 (1) ![]() ; (2) 0.48
; (2) 0.48
19、(1)略;
(2)![]()
20、(1)![]() ; (2)
; (2)![]()
21、(1)![]() ;
(2)
;
(2)![]()