湖北省西部地区重点中学联考<<函数与集合>>单元测试卷
（2005.9）
第Ⅰ卷（选择题，共60分）
一、选择题（本大题共12小题，每小题5分，共60分）
1、设函数
与函数
的图象关于
对称，则的表达式为 （ ）
(A)
(B)
(C)
(D)
2、设
（ ）
3、 指数函数y=f(x)的反函数的图象过点（2，－1），则此指数函数为 （ ）
A、
B、
C、
D、
4、
已知函数
>0，则
的值
（ ）
A、一定大于零 B、一定小于零 C、等于零 D、正负都有可能
5、
若函数
在区间（－1，0）上有
的递增区间是
（ ）
6、
已知
的关系是
（ ）
7、
已知
的实根个数是
（ ）
A、1个 B、2个 C、3个 D、1个或2个或3个
8、
若
的最小值为
（ ）
9、
已知函数
是定义在R上的奇函数，当
的值为 （ ）
A、2 B、 －2 C、3 D、－3
10、若方程
的取值范围是
（ ）
11、
的值是 （ ）
A、2
B、
12、设
的值为 （ ）
A、1
B、－1
C、－
D、
第Ⅱ卷（非选择题，共90分）
二、填空题（本大题共4小题，每小题4分，共16分）
13、使函数
具有反函数的一个条件是_________。（只填上一个条件即可，不必考虑所有情形）。
14、函数
的单调递减区间是________________________。
15、已知是定义在
上的偶函数，并且
，当
时，
，则
_________________
16、关于函数
有下列命题：①函数的图象关于
轴对称；②在区间
上，函数是减函数；③函数的最小值为
；④在区间
上，函数是增函数.其中正确命题序号为_______________
三、解答题（本大题共6小题，共74分。解答应写出文字说明、证明过程或演算步骤。）
17、（本小题满分12分）已知函数f(x)=ax+
(a>1)
（1） 证明：函数f(x)在(-1,+∞)上为增函数；
（2） 用反证法证明f(x)=0没有负数根。
18、（本小题满分12分）
已知f（x）＝2x－1的反函数为
（x），g（x）＝log4（3x＋1）.
(Ⅰ)若f-1（x）≤g（x），求x的取值范围D；
(Ⅱ)设函数H（x）＝g（x）－（x），当x∈D时，求函数Ｈ（x）的值域.
19、（本小题满分12分）函数f(x)=loga(x－3a)(a＞0,且a≠1),当点P（x,y)是函数y=f(x)图象上的点时，Q（x－2a,－y)是函数y=g(x)图象上的点.
（Ⅰ）写出函数y=g(x)的解析式.
（Ⅱ）当x∈［a+2,a+3］时，恒有f(x)－g(x)≤1,试确定a的取值范围.
20、（本小题12分）某化妆品生产企业为了占有更多的市场份额，拟在2002年度进行一系列促销活动，经过市场调查和测算，化妆品的年销量x万件与年促销ｔ万元之间满足3－x与ｔ＋1成反比例，如果不搞促销活动，化妆品的年销量只能是1万件，已知2002年生产化妆品的设备折旧，维修等固定费用为3万元，每生产1万件化妆品需再投入32万元的生产费用，若将每件化妆品的售价定为：其生产成本的150%“与平均每件促销费的一半”之和，则当年生产的化妆品正好能销完.
(Ⅰ)将2002年的利润y(万元)表示为促销费ｔ(万元)的函数；
(Ⅱ)该企业2002年的促销费投入多少万元时，企业的年利润最大?
(注：利润＝销售收入—生产成本—促销费，生产成本＝固定费用＋生产费用)
21、（本小题满分12分）
已知f(x)在（－1，1）上有定义，f(
)=－1，且满足x,y∈(－1,1)有f(x)+f(y)=f(
)
（Ⅰ）证明：f(x)在（－1，1）上为奇函数；
（Ⅱ）对数列x1=,xn+1=
,求f(xn);
（Ⅲ）求证
22、（本小题满分14分）对于函数f（x），若存在x0∈R,使f（x0）＝x0成立，则称x0为
f（x）的不动点.如果函数f（x）＝ax2＋bx＋1（a＞0）有两个相异的不动点x1，x2.
(Ⅰ)若x1＜1＜x2，且ｆ（x）的图象关于直线x＝m对称,求证：＜m＜1；
(Ⅱ)若｜x1｜＜2且｜x1－x2｜＝2，求b的取值范围.
参考答案
一、DAABC，DBAAC，CD
二、13．x≥2, 14 (2,+∞) , 15 2.5 , 16 (1) (3) (4)
17.略
18. 解：(Ⅰ)∵
∴
(x＞-1) 2分
由
≤g（x） ∴
14分
解得0≤x≤1 ∴D＝［0，1］ 6分
(Ⅱ)H（x）＝g（x）－
9分
∵0≤x≤1 ∴1≤3－
≤2
∴0≤H（x）≤ ∴H（x）的值域为［0，］ 12分
19.解：（Ⅰ）设P(x0,y0)是y=f(x)图象上点，Q（x,y）,则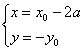
，
∴
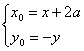∴－y=loga(x+2a－3a)，∴y=loga
(x＞a)
5分
（Ⅱ）
∴x＞3a
∵f(x)与g(x)在［a+2,a+3］上有意义.
∴3a＜a+2
∴0＜a＜1 6分
∵f(x)－g(x)≤1恒成立
loga(x－3a)(x－a)≤1恒成立.
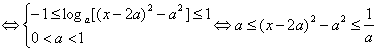8分
对x∈［a+2,a+3］上恒成立，令h(x)=(x－2a)2－a2
其对称轴x=2a,2a＜2,2＜a+2
∴当x∈［a+2,a+3］
hmin(x)=h(a+2)，hmax=h(a+3)
∴原问题等价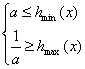
10分
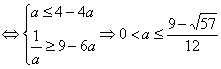12分
20.解：（Ⅰ）由题意：
将
2分
当年生产x(万件)时，年生产成本＝年生产费用＋固定费用＝32x＋3＝32（3－
）＋3，当销售x（万件）时，年销售收入＝150%［32（3－＋3］＋
由题意，生产x万件化妆品正好销完
∴年利润＝年销售收入－年生产成本－促销费
即
（t≥0）
6分
（Ⅱ）∵
≤50－
＝42万件
10分
当且仅当
即t＝7时，ymax＝42
∴当促销费定在7万元时，利润增大. 12分
21.（Ⅰ）证明：令x=y=0，∴2f(0)=f(0),∴f(0)=0
令y=－x,则f(x)+f(－x)=f(0)=0
∴f(x)+f(－x)=0 ∴f(－x)=－f(x)
∴f(x)为奇函数 4分
（Ⅱ）解：f(x1)=f()=－1，f(xn+1)=f()=f(
)=f(xn)+f(xn)=2f(xn)
∴
=2即{f(xn)}是以－1为首项，2为公比的等比数列
∴f(xn)=－2n－18分
（Ⅲ）解：
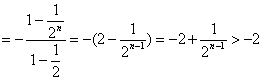10分
而
∴
12分
22.(Ⅰ)证明：g（x）＝f（x）－x＝ax2＋（b－1）x＋1且a＞0 ∵x1＜1＜x2＜2
∴（x1－1）（x2－1）＜0即x1x2＜（x1＋x2）－1 2分
于是
＞
［（x1+x2）-1］=
4分
又∵x1＜1＜x2＜2 ∴x1x2＞x1于是有ｍ＝（x1＋x2）－x1x2＜（x1＋x2）－x1＝x2＜1 ∴＜m＜1
6分
(Ⅱ)解：由方程
＞0，∴x1x2同号
（ⅰ）若0＜x1＜2则x2－x1＝2
∴x2＝x1＋2＞2 ∴g（2）＜0
即4a＋2b－1＜0 ①
又(x2－x1)2＝
8分
∴
，（∵a＞0）代入①式得
＜3－2b，解之得：b＜
10分
(ⅱ)若－2＜x1＜0，则x2＝－2＋x1＜－2 ∴g（－2）＜0，即4a－2b＋3＜0 ②
又代入②得＜2b－1解之得b＞
综上可知b的取值范围为
14分