湖北省宜昌市2005—2006学年度高三年级调研考试
数学(文)试卷
2006.1
YCY
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）共两部分。满分150分，考试时间120分钟.
第Ⅰ卷（选择题，共60分）
一、选择题（每小题所给的四个选项中，只有一个符合题目要求，每小题5分，共60分）
1．已知函数
的图像经过点
，则常数
的值为 （ ）
A．2
B．4 C．
D． 
2．在等差数列
中 ，已知公差
，
，则
（ ）
A．2011 B．2010 C．2009 D．2008
3．已知集合
，
，则集合
的子集个
数为 （ ）
A．4 B．6 C．8 D． 9
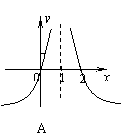
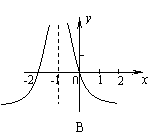
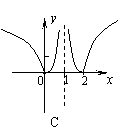
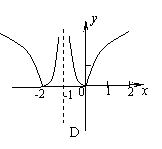4．函数
的图像大致是
（ ）
5．函数
的最小正周期是
（ ）
A．
B．
C．
D．
6．已知双曲线的两个焦点为
，
，P是此双曲线上的一点，且
， 
，则该双曲线的方程是
（ ）
A．
B．
C．
D．
7．已知直线
和圆
，则直线与圆的交点个数为 （ ）
A．至少有一个 B．至多有一个 C．有且只有一个 D．0个
8．计算机是将信息转换成二进制进行处理的，所谓二进制即“逢二进一”，如（1101）2表示二进制的数，将它转换成十进制数的形式是1×23+1×22+0×21+1×20=13，那么将二进制数
转换成十进制数是 （ ）
A．217－2 B．216－1 C．216－2 D．215－1
9．
是
的
（ ）
A．充分而不必要条件 B．必要而不充分条件
C．充要条件 D．既不充分也不必要条件
10．已知
且
，则下列不等式中恒成立的是
（ ）
A．
B．
C．
D．
11．使
为奇函数，且在
上是减函数的
的一个值
是 （ ）
A．
B．
C．
D．
12．设函数f （x）＝ax2＋bx＋c对任意实数t都有f （2＋t）＝ f （2－t）成立，在函数值
f（－1），f（1），f（2），f（5）中的最小的一个不可能是 （ ）
A．f （－1） B．f （1） C．f （2） D．f （5）
第Ⅱ卷（非选择题，共90分）
二、填空题（本大题共4小题，每小题4分，共16分，把答案填在题中横线上）
13．函数
的单调递减区间为
.
14．已知点
（3，2）在椭圆
上，则以点为顶点的椭圆的内接矩形
的面积是
.
15．光线透过一块玻璃板，其强度要减弱
，要使光线的强度减弱到原来的
以下，至少有这样的玻璃板 块.（参考数据：
16．设函数f （x）的定义域为D，如果对于任意的
，使
成立，则称函数f （x）在D上均值为C，给出下列四个函数 ①
②
③
④
则满足在其定义域上均值为2的函数是 .
三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）
17．（本题满分12分）已知
，
（Ⅰ） 求
；
（Ⅱ）求使
成立的
的取值集合．
18．（本题满分12分）
已知是各项都是正数的等比数列，且
，又知
.
（Ⅰ）求证数列
是一个等差数列，并求数列的前
项和为
；
（Ⅱ）求数列
的前项和
.
19．（本题满分12分）
设向量
，其中
为锐角.
（Ⅰ）求
；
（Ⅱ）当
为何值时，
的模最小？最小值是多少？
20．（本题满分12分）
已知函数
.
（Ⅰ） 求
；
（Ⅱ） 若
，函数
的图象能否总在直线
的下方？说明理由；
（Ⅲ）若函数在
上是增函数，
是方程
的一个根，
求证：
.
21．（本题满分12分）
宜昌市某企业2005年底共有员工2000人，当年的生产总值为1.6亿元，该企业规划从2006年起的10年内每年的总产值比上一年增加1000万元；同时为扩大企业规模，该企业平均每年将录用m（m＞50，m∈N）位新员工；经测算这10年内平均每年退休的员工为50人，设从2006年起的第x年（2006年为第1年）该企业的人均产值为y万元。
（Ⅰ）写出y与x之间的函数关系式y=f （x），并注明定义域；
（Ⅱ）要使该企业的人均产值在10年内每年都有增长，则每年录用新员工至多为多少人？
22．（本题满分14分）
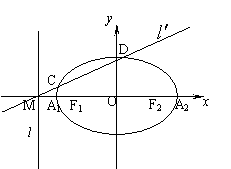
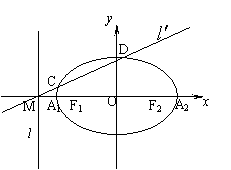
如图，已知椭圆的中心在坐标原点，焦点
在轴上，长轴
的长为4，左准线
与轴的交点为M，
．
（Ⅰ）求椭圆的方程；
（Ⅱ）过点M的直线
与椭圆交于C、D两点，若
，求直线的方程；
（Ⅲ）若点P为上的动点，求∠F1PF2最大值．
 |
参考答案
第Ⅰ卷（选择题 共60分）
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | A | C | A | B | C | A | B | A | C | C | B |
第Ⅱ卷（非选择题 共90分）
二、填空题
13． 
14． 24 15． 11 16． ①③
三、解答题
17． 解答：（Ⅰ）
………………………………………………6分
（Ⅱ）由得：
，解得
.…………10分
即使成立的的取值集合： 
. ………………………………12分
18．解答：（Ⅰ） 
，
，
故数列是一个等差数列， ……………………………………………………3分
.………………………………………………6分
（Ⅱ） 
, …………………………………………8分
.……………………12分
19．解答：（Ⅰ） 
.………………………………………………………………………6分
（Ⅱ） 
则
，………………………………………………………………10分
当
时，
最小为
，从而的模最小值为
. ………………………12分
20．解答：（Ⅰ） 
. …………………………………………………2分
（Ⅱ）
时，
，令
得：
由于
，
，
所以函数的图象不能总在直线的下方. ………………………………6分
（Ⅲ）因函数在上是增函数，
在区间上恒成
立，即
在区间上恒成立，
，……………………………8分
又由
得
，
而
，
即.…………………………………………………………………………12分
21．解答：（Ⅰ）从2006年起的第x年（2006年为第1年）该企业的总产值是16000＋1000x（万元），此时该企业的员工数为2000＋（m－50）x（人），………………… 2分
所以
，（1≤x≤10，x∈N）， …………………………………5分
（Ⅱ） 依题意，该函数为定义域上的增函数
任取1≤x1＜x2≤10，x1、x2∈N，
f（x1）－f （x2）
= 
=
……………………8分
令f （x1）－f （x2）＜０，∵1≤x1＜x2≤10，m＞50，
∴x1－x2＜0，2000＋（m－50）x1＞0， 2000＋（m－50）x2＞0 ，
∴
＞０，解得：m＜175
∵m∈N，∴该企业每年录用新员工至多为174人． ……………………… 12分
22．解答：（Ⅰ）设椭圆方程为
，半焦距为
，
则
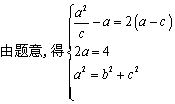
………………………………………………5分
（Ⅱ） 点M的坐标为
，设C、D两点的坐标分别为
，
的方程为
，代入椭圆方程并整理得：
①
则
②
由 得：
，
③
又
，
④
由②③④得：
，……………………8分
解得：
，代入①有检验有
，
得所求直线的方程为
………………………………………10分
（Ⅲ）
