湖南省示范性高中2006届高三八校第二次联考
文科数学试题(II)
命题: 株州市二中 岳阳市一中 常德市一中 雅礼中学
湘潭市一中 郴州市一中 邵阳市二中 衡阳市一中
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.
参考公式: 正棱锥、圆锥的侧面积公式
如果事件A、B互斥,那么
![]()
P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么 其中,c表示底面周长、l表示斜高或
P(A·B)=P(A)·P(B) 母线长
如果事件A在1次实验中发生的概率是 球的体积公式
P,那么n次独立重复实验中恰好发生k
![]()
次的概率 其中R表示球的半径
![]()
第I卷(选择题 共50分)
一.选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合要求的.
1.设![]()
A.[2,4] B.![]() C.[-2,4] D.
C.[-2,4] D.![]()
2.已知![]() ,则
,则![]()
A.在区间(-1,+∞)上是增函数 B.在区间(-∞,1) 上是增函数
C.在区间(-1,+∞)上是减函数 D.在区间(-∞,1) 上是减函数
3.某单位有职工160人,其中有业务人员120人,管理人员16人,后勤人员24人,为了了解职工的某种情况,要从中抽取一个容量为20的样本,若要用分层抽样的方法抽取的业 务人员、管理人员、后勤人员的人数分别为
A.7、6、7 B.15、2、3 C.10、6、4 D.17、1、2
4.已知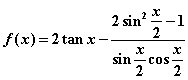 ,则
,则![]() 的值为
的值为
A.![]() B.
B.![]() C.4 D.8
C.4 D.8
5.对于![]() 的一切值,
的一切值,![]() 恒成立的
恒成立的
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
6.过点M(-2,0)的直线m与椭圆交于P1,P2两点,线段P1P2的中点为P,设直线m的斜率为k1(![]() ),直线OP的斜率为k2,则k1k2的值为
),直线OP的斜率为k2,则k1k2的值为
A.2 B.-2 C.![]() D.-
D.-![]()
7.在北纬45°的纬线圈上有A、B两地,A在东经1100,B在西经1600,设地球半径为R,则A、B两地的球面距离是
A.![]() R B.
R B.![]() R C.
R C.![]() R D.πR
R D.πR
8.已知直线![]() 与圆
与圆![]() 交于
交于![]() 两点,且
两点,且![]() ,其中
,其中![]() 为原点,则实数
为原点,则实数![]() 的值为
的值为
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
9.某医药研究所研制了5种消炎药X1、X2、X3、X4、X5和4种退烧药T1、T2、T3、T4,现从中取出两种消炎药和一种退烧药同时使用进行疗效试验,但又知X1、X2两种消炎药必须同时搭配使用,但X3和T4两种药不能同时使用,则不同的试验方案有
A.16 B.15 C.14 D.13
10.函数![]() 的定义域为
的定义域为![]() ,若满足1
,若满足1![]() 在
在![]() 内是单调函数;2存在
内是单调函数;2存在![]() ,使得
,使得![]() 在
在![]() 上的值域为
上的值域为![]() ,则
,则![]() 叫做闭函数.现在
叫做闭函数.现在![]() 是闭函数,则
是闭函数,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二.填空题:本大题共5小题,每小题4分,共20分,把答案填在题中横线上.
11.![]() 的展开式的第4项是 .
的展开式的第4项是 .
12.数列![]() 中,
中,![]() 是其前
是其前![]() 项和,若
项和,若![]() ,则
,则![]() = .
= .
13.在四棱锥P-ABCD中,ABCD为矩形,AB=3,AD=4,PA⊥平面ABCD,PA=4,Q是PA的中点,则点P到平面BQD的距离为 .
14.实数![]() 满足
满足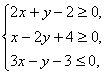 则
则![]() 的最小值是
.
的最小值是
.
15.已知函数![]() ,则
,则
![]() 的图象的交点个数为 .
的图象的交点个数为 .
三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的值域;
的值域;
(2)将![]() 的图象按向量
的图象按向量![]() 平移,使得平移后的图象关于原点对
平移,使得平移后的图象关于原点对
称,求出向量![]() .
.
17.某班有两个课外活动小组,其中第一小组有足球票6张,排球票4张;第二小组有足球票4张,排球票6张.甲从第一小组的10张票中任抽1张,乙从第二小组的10张票中任抽1张.
(1)两人都抽到足球票的概率是多少?
(2)两人中至少有1人抽到足球票的概率是多少 ?
18.(本小题满分14分)
如图,直平行六面体![]() 的底面
的底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,E为
,E为![]() 的中点,二面角
的中点,二面角![]() 为
为![]() .
.
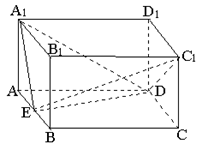 (1)求证:面
(1)求证:面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
19.已知正项数列{an}满足:![]() ,且
,且![]() ,
,
(1)求数列{an}的通项公式;
(2)求证:![]() .
.
20.已知双曲线C:![]() 的右准线L经过抛物线E:y2=2PX(P>0)的焦点F,且L与E
的右准线L经过抛物线E:y2=2PX(P>0)的焦点F,且L与E
在X轴上方交于M,双曲线C的右焦点为F2,若△MFF2为等腰直角三角形.
(1)求双曲线C的离心率e;
(2)若双曲线C与抛物线E在X轴上方交于N,且![]() =4(
=4(![]() ),求C与E的方程;
),求C与E的方程;
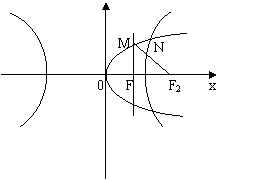 (3)求直线NF与MF2交点的轨迹方程.
(3)求直线NF与MF2交点的轨迹方程.
21.已知f(x)=![]()
(1)当a=0,b=-3时,求与直线4x+15y-3=0垂直的曲线y=f(x)的切线方程;
(2)若存在实数b使曲线y=f(x)在x∈ [1,4]上存在斜率为-8的切线且切点在直线y=1的上方,求a的取值范围.
文科参考答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | D | C | D | C | D | B | C | C | D |
| 题号 | 11 | 12 | 13 | 14 | 15 | |||||
| 答案 |
|
| |
| 4 | |||||
16解:(1)化简函数得![]() , 由已知有
, 由已知有![]() ,………6分
,………6分
所以,![]() 的值域为
的值域为![]() .
…………7分
.
…………7分
(2)由图象变换得![]() .
…………9分
.
…………9分
而平移后的图象关于原点对称,所以![]() 且
且![]() , …………11分
, …………11分
而![]() ,所以
,所以![]() ,即
,即![]() .
…………12分
.
…………12分
17解:记“甲从第一小组的10张票中任抽1张,抽到足球票”为事件A,则
“甲从第一小组的10张票
任抽1张,抽到排球票”为事件![]() ,
,
“乙从第二小组的10张票中任抽1张,抽到足球票”为事件B,
“乙从第二小组的10张票中任抽1张,抽到排球票”为事件![]() ,A与B是相互独立事件…2分
,A与B是相互独立事件…2分
![]() 6分
6分
(I) ![]()
答:两人都抽到足球票的概率是![]() .……………………9分
.……………………9分
(II)甲、乙两均未抽到足球票(事件![]() 发生)的概率为;
发生)的概率为; ![]()
∴两人中至少有1人抽到足球票的概率为:![]()
答:两人中至少有1人抽到足球票的概率是![]() .………………………………12分
.………………………………12分
18(1)证:![]() ,
,![]()
![]()
又![]()
![]()
故 面![]() 。…………6分
。…………6分
(2)由三垂线定理可知![]()
![]() 为二面角为
为二面角为![]() 的平面角
的平面角
![]()
![]()
![]()
又![]() 故
故![]() 所成角的大小为二面角
所成角的大小为二面角![]() 的大小
的大小
而![]()
又![]()
![]()
![]() ,
,![]()
![]()
![]() 的余弦值为
的余弦值为![]() .…………14分
.…………14分
19解:.
![]()
![]()
![]() 20解:
20解:![]()
![]()
![]()
![]() -
-![]() =1 M N
=1 M N
![]() ⑴
⑴ ![]() =p/2
=p/2 ![]() 2a2=b2
2a2=b2
![]() b=
b= ![]() a
O F F2 X
a
O F F2 X
![]() =p
∴c=
=p
∴c=![]() a ∴e=
a ∴e=![]() =
=![]() p=
p=![]() a
a
![]() ⑵ N(X0,Y0),则 Y02=2P X0
⑵ N(X0,Y0),则 Y02=2P X0 ![]() y02=2p x0=
y02=2p x0=![]() ax0
ax0 ![]() 2x02-
2x02-![]() ax0=2a2
ax0=2a2
![]() -
-![]() =1
=1 ![]() 2x02-y02=2a2
2x02-y02=2a2
![]() x0=
x0=![]() a(舍去x0=
a(舍去x0= ![]() a ) ∴y0 =2a(∵y0>0)
a ) ∴y0 =2a(∵y0>0)
![]()
![]() =-
=-![]() a2 +
a2 + ![]() a2=4(
a2=4(![]() -1)
-1)
a2 =3 ,b2 =6 , p=2
∴双曲线C:![]() ,抛物线E:y2=4X
。
,抛物线E:y2=4X
。
![]() ⑶ NF:y=
⑶ NF:y=![]() (x
(x![]() a) ∴y=
a) ∴y=![]() x-a
x-a
MF2:y=-(x-![]() a) y=-x+
a) y=-x+![]() a y=(
a y=(![]() -1)x (x>0)
-1)x (x>0)
∴直线NF与MF2的轨迹方程为:y=(![]() -1)x (x>0)
-1)x (x>0)
21解: ⑴f(x)= x3-3x+1, 又f'(x)= 3x2-3=![]() → x2 =
→ x2 =![]() → x=±3/2
→ x=±3/2
∵x3-3x>1 ∴x=-3/2
又f(-3/2)=9/8 , ∴切点为(-3/2 , 9/8)
∴存在与直线4x+15y-3=0垂直的切线,其方程为
15x-4y-23=0 或 15x-4y+31=0
⑵ ∵f(x) = x3+ax2+bx+1在直线y=1的上方
∴x3+ax2+bx+1>1 → x3+ax2+bx>0
又f'(x)= 3x2+2ax + b=-8 → b=-3x2-2ax-8
x3+ax2+bx= x3+ax2+x(-3x2-2ax-8)= -2x3-ax2-8x>0在x∈(1 , 4)上有解
→ 2x2+ax2+8<0在x∈(1 , 4)上有解 → a<-2x-8/x在x∈(1 , 4)上有解
∴a<(-2x-8/x)max , x∈(1 , 4)
而-2x-8/x=-2(x+4/x)≤-4![]() =-8 (当x=2时取=)
=-8 (当x=2时取=)
∴a<-8