华南师范大学附中 2005 学四月份高三
数学试题
考试时间：120分钟 满分150分
日期：2005年4月12日 星期二
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。
第Ⅰ卷（选择题 共50分）
注意事项：
1．答第Ⅰ卷前，考生务必将自己的姓名、准考号、考试科目用铅笔涂写在答题卡上。
2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡
皮擦干净后，再选涂其它答案，不能答在试题卷上。
参考公式：
如果事件A、B互斥，那么 球的表面积公式
P（A+B）= P（A）+ P（B） S = 4πR2
如果事件A、B相互独立，那么 其中R表示球的半径
P（A·B）= P（A）·P（B） 球的体积公式
如果事件A在一次试验中发生的概率是P 
那么n次独立重复试验中恰好发生k次的概 率 其中R表示球的半径
一、选择题：本大题共 10 小题；每小题 5 分，满分 50 分。在每小题给出的四个选项中，只有一项是符合题目要求的。请将答案填入答题卡中。
1、若函数f(x) = + 2x
+ log2x的值域是 {3, －1, 5 + , 20}，则其定义域是
(A) {0，1，2，4} (B)
{，1，2，4} (C)
{，2，4} (D)
{，1，2，4，8}
2、6名运动员站在6条跑道上准备参加比赛，其中甲不能站在第一道也不能站在第二道，乙必须站在第五道或第六道，则不同排法种数共有
(A) 144 (B) 96 (C) 72 (D) 48
3、在平面直角坐标系内，将直线l向左平移3个单位，再向上平移2个单位后，得到直线l¢，l 与l¢ 间的距离为 ，则直线l的倾斜角为
(A) arctan (B) arctan (C) p－arctan (D) p－arctan
4、设F1, F2是双曲线 －y 2 = 1的两个焦点，P在双曲线上，当△F1PF2的面积为1时，·的值为
(A) 0 (B) 1 (C) (D) 2
5、若 a Î ( , p)，则不等式 log sin a (1－x 2 ) > 2的解集是
(A) {x －cos a < x < cos a} (B) {x x > cos a 或 x < －cos a }
(C) {x －1 < x < －cos a 或 cos a < x < 1 } (D) {x －1 < x < cos a 或 －cos a < x < 1 }
6、在长方体ABCD－A1B1C1D1中，AB = 4，BC = 6，AA1 = 8，点E在AB上，AE = 1，点F在BC上，BF = 3．过EF作与底面成30°角的截面，则截面面积是
(A) 6 (B) 13 (C) 3或 13 (D) 3或 9
7、把长为12厘米的细铁丝截成两段，各自围成一个正三角形，则这两个正三角形面积之和的最小值是
(A) cm 2 (B) 4 cm 2 (C) 3cm 2 (D) 2cm 2
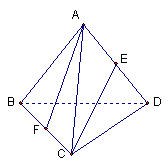8、如图，在棱长都相等的四面体
中，
、
分别为棱
、
的中点，连接
、
，则直线、所成角的余弦值为
(A) (B)
(C)
(D)
9、使可行域为 的目标函数z = ax + by (ab ≠ 0)，在x = 2, y = 2取得最大值的充要条件是
(A) a ≤b
(B) a ≤ b (C) a ≥b (D) a ≥ b
10、已知tana , tanb 是方程x2
+ 3x + 4 = 0的两根，且a , b Î (－, )，则a + b =
(A) (B)
－或 (C)
或－ (D)
－
二、填空题（本大题共4小题，每小题5分，共20分）
11、已知复数z满足 z + 1 = 1，并且 是纯虚数，则复数z的值为***．
12、已知
，若记
为
的反函数，且
则
*** ．
13、等差数列 {an} 的前3项和为21，其前6项和为24，则其首项a1 = ________；数列 { an} 的前9项和等于***．
14、函数 f (x) = sin ( x + ) 的最小正周期为***；其图象的位于y轴右侧的对称轴从左到右分别为l1, l2, l3, …，则l3的方程是***．
三、解答题：本大题共 6 小题；共 80分。解答应写出文字说明、证明过程或演算步骤。
15、(本小题满分12分)
已知向量
=（sinB，1－cosB)，且与向量
= （2，0）所成角为
，其中A、B、C是
△ABC的内角．
（Ⅰ）求角Ｂ的大小；
（Ⅱ）求sinA + sinC的取值范围．
16、(本小题满分12分)
两个人射击，甲射击一次中靶概率是p1，乙射击一次中靶概率是p2，已知 , 是方程
x2－5x + 6 = 0的根，若两人各射击5次，甲的方差是 ．
(1) 求 p1, p2的值；
(2) 两人各射击2次，中靶至少3次就算完成目的，则完成目的的概率是多少？
(3) 两人各射击一次，中靶至少一次就算完成目的，则完成目的的概率是多少？
17、(本小题满分14分)
在三棱锥P－ABC中，PA = PB = PC, BC
= 2a, AC = a, AB = a，点P到平面ABC的距离为 a．
(1) 求二面角P－AC－B的大小；
(2) 求点B到平面PAC的距离．
18、(本小题满分14分)
某一电视频道在一天内有
次插播广告的时段，一共播放了
条广告，第1次播放了1条和余下的
条的
，第二次播放了2条以及余下的，第3次播放了3条以及余下的，以后每次按此规律插播广告，在第x次播放了余下最后的条（
）。
（Ⅰ）设第
次播放后余下
条，这里
，求与
的递推关系式；
（Ⅱ）求这家电视台这一天播放广告的时段与广告的条数。
19、(本小题满分14分)
已知 f (x) 是奇函数，且x < 0时，f (x) = 2 ax + ．
(1) 求x > 0时，f (x) 的表达式；
(2) a为何值时，f (x) 在 (0, 1] 上为增函数；
(3) 是否存在实数a，使 f (x) 在 (0, + ¥) 上取得最大值－9 ？
20、(本小题满分14分)
在平面直角坐标系中，
为坐标原点，已知两点
、
，若点
满足
（
），点的轨迹与抛物线
交于
、
两点.
（Ⅰ）求证：
⊥
；
（Ⅱ）在轴上是否存在一点
(m ≠ 0)，使得过点
任作抛物线的一条弦，并以该弦为直径的圆都过原点。若存在，请求出
的值及圆心的轨迹方程；若不存在，请说明理由.
2005年4月12日试题答案
一、选择题
1、B．因为f(x)是增函数，又f( ) = －1，f(1) = 3，f(2) = 5 + ，f(4) = 20，
故定义域是 {，1，2，4}
2~8、ABADCDC
9、A．画出可行区域，直线l:ax + by = 0的斜率为－，要使目标函数z = ax + by在x = 2,y = 2时，取得最大值，必须且只需－≤1，且直线l向上平移时，纵截距变大，所以必须且只需－≤1且b>0。
10、D．易错：忽视tana ,tanb 是方程x2 + 3x + 4 = 0的两负根 Þ a ,b Î (－,0)
二、填空题
11、0或－2 12、－2 13、9；41 14、12p；x = 13p
三、解答题
15、解：（Ⅰ）∵ =（sinB，1－cosB) , 且与向量=（2，0）所成角为
∴ 
， 2分
∴ tan = ， 4分
又∵ 0<B<p Þ 0< < ，
∴ = ，
∴ B = 。 6分
（Ⅱ）由（Ⅰ）可得A + C = ，
∴
， 8分
∵
，
∴
， 10分
∴
，
当且仅当
。 12分
16、解：(1) 由题意可知 x甲 ~ B(5, p1)，
∴ Dx甲 = 5p1 (1－p1) = Þ p12－p1 + = 0 Þ p1 = ．2分
又 ·= 6，
∴ p2 = ． 3分
(2) 两类情况：
共击中3次概率
C ( ) 2 ( ) 0×C ( ) 1 ( ) 1 + C ( ) 1 ( ) 1×C ( ) 2 ( ) 0 = ； 5分
共击中4次概率
C ( ) 2 ( ) 0×C ( ) 2 ( ) 0 = ． 7分
所求概率为 + = ． 8分
(3) 设事件A, B分别表示甲、乙能击中．
∵ A, B互相独立， 9分
∴ P(`A·`B ) = P(`A ) P(`B ) = (1－P(A) )(1－P(B) ) = (1－p1)(1－p2) = ×= ．
11分
∴ 1－P(`A·`B ) = 为所求概率． 12分
17、
解：(1) 法一：由条件知△ABC为直角三角形，且∠BAC = 90°，
∵ PA = PB = PC，
∴ 点P在平面ABC上的射影是△ABC的外心，
即斜边BC的中点E．2分
取AC中点D，连PD, DE, PE．
∵ PE⊥平面ABC，DE⊥AC (∵ DE∥AB),
∵ AC⊥PD． 4分
∴ ∠PDE为二面角P－AC－B的平面角． 5分
又PE = a ，DE = a ，
∴ 
tan ∠PDE = = = ，
∴ ∠PDE = 60°．
故二面角P－AC－B的大小为60°． 8分
法二：由条件知△ABC为直角三角形，且∠BAC = 90°，
∵ PA = PB = PC，
∴ 点P在平面ABC上的射影是△ABC的外心，即斜边BC的中点．
设O为BC中点，则可证明PO⊥平面ABC．2分
建立如图直角坐标系，则
A( a, a, 0), B(－a, 0, 0), C(a, 0, 0), D(0, 0, a)．
= (－a, a, 0), = ( －a, a, a)．4分
取AC中点D，连PD, DO, PO．
∵ AB⊥AC,
又PA = PCÞ PD⊥AC．
∴ cos < , > 即为二面角P－AC－B的余弦值． 6分
而 cos < , > = = ．
∴ 二面角P－AC－B的大小为 60°． 8分
(2) 法一：PD = = = a．
S△APC = AC·PD = a 2． 10分
设点B到平面PAC的距离为h，则由VP－ABC = VB－APC 得
S△ABC·PE = S△ABC·h Þ h = = = a．
故点B到平面PAC的距离为 a． 14分
法二：点E到平面PAC的距离容易求得为 a，而点B到平面PAC的距离是其两倍．
∴ 点B到平面PAC的距离为 a． 14分
18、解：（Ⅰ）依题意有第次播放了
， 2分
因此
。 5分
（Ⅱ）∵
= 1 + 2×+ ( )2a2
= ┅
= 1+ 2×+ 3×( )2 + ┅ + x×( )x－1 + ( )xaz ，8分
∵
∴ y = 1+ 2×+ 3×( )2 + ┅ + x×( )x－1, 10分
∴ y = + 2×( )2 + 3×( )3 + ┅ + x×( )x ，
用错位相减法求和得：
, 12分
∵
，∴
，即
.
13分
答：这家电视台这一天播放广告的时段= 7与广告的条数= 49。 14分
19、解：(1) 设x > 0，则－x < 0，∴ f (－x) = 2a(－x) + = －2ax + ．2分
而 f (x) 是奇函数，
∴ f (x) = －f (－x) = 2ax－ (x > 0)． 4分
(2) 由(1)，x > 0时，f (x) = 2ax－ ，∴ f /(x) = 2a + ．6分
由 f./ (x) ≥ 0得a ≥ －．
而当0 < x ≤ 1时，(－ )max = －1．∴ a > －1． 8分
(3) 由 f ¢ (x) = 2a + 知，
当a ≥ 0时，在 (0, + ¥) 上，f ¢ (x) 恒大于0，故 f (x) 无最大值； 10分
当a < 0时，令f ¢ (x) = 0 得 x = ．
易得 f (x) 在 (0, + ¥) 的增减性如下表所示：
| x | （0，） |
| （， + ¥） |
| f ¢ (x) | + | 0 | － |
| f (x) | 递增 | 极大 | 递减 |
12分
令 f ( ) = 2a·－= －9，即 3 = 9，得a = ±3，
当a = －3时，x = >0，
∴ a = －3时，在 (0, + ¥) 上有 f (x) max = f ( ) = －9．14分
20、解：(Ⅰ)由（）知点的轨迹是
、
两点所在的直线，
故点的轨迹方程是：
即
。 2分
由
，
设A(x1，y1)，B(x2，y2)，则
，
，
∴
，
∴
，故 ⊥。
6分
(Ⅱ) 存在点P(4,0)，使得过点任作抛物线的一条弦，以该弦为直径的圆都过原点。7分
由题意知弦所在的直线的斜率不为零， 8分
故设弦所在的直线方程为
， 代入 y2 = 4x 得 
，
∴ 
，
，
∴ 
，
∴
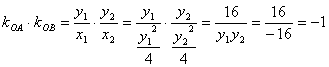， 故以
为直径的圆都过原点。 10分
设弦的中点为
， 则
， 
，
，
∴弦的中点的轨迹方程为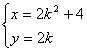
，
消去得 
。 14