淮安市2004—2005学年度高三第三次调查测试
数 学 试 题 05.4
本试卷分为第I卷（选择题）和第II卷（非选择题）两部分，满分150分。考试时间120分钟。
第I卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，满分60分。每小题的四个选项中有且只有一个是正确的，请把正确答案填涂在答题卡的指定位置。
1．若直线
不关于原点对称，则必有
（ ）
A．
B．
C．
D．
2．已知双曲线
的两条渐近线互相垂直，则这条双曲线的离心率等于
（ ）
A．
B．
C．
D．2
3．已知向量
，且c//d，则实数x的值等于（ ）
A．
B．
C．
D．
4．已知函数
的反函数为g (x) ，若数列{an}满足
，则数列{an}的前n项和Sn=
（ ）
A．
B．
C．
D．
5．已知两条不重合直线a,b，三个不重合平面α、β、γ，则下面四个命题中真命题是 （ ）
A．
B．
则
C．
D．
6．已知集合
，规定运算“*”，若a∈M, b∈M, 则a*b∈M，那么运算“*”可能是
（ ）
A．加法 B．减法 C．乘法 D．除法
7．若
被7除的余数为2，则正整数n的最小值等于
（ ）
A．1 B．2 C．3 D．4
8．已知函数
，且g (x) 满足
，若f (x) 的最大值、最小值分别为M、N，则M+N= （ ）
A．0 B．2 C．4 D．6
9．设x、m∈R，则“m > 1”是“关于x的不等式x－m>1－x的解集为R”的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
10．已知函数
的图象与直线y=－1的交点中，距离最近的两点间距离为
，则函数f (x)的最小正周期等于
（ ）
A．
B．
C．
D．
11．已知A、B分别为椭圆
的左、右顶点，P是椭圆上第一象限的任一点，若
，则必有
（ ）
A．
B．
C．
D．
12．如果甲的身高或体重至少有一项比乙大，则称甲比乙“好”，若在5名男同学中某人比其他4人“好”，就称这同学为“最好”，那么在5名男同学中，“最好”的男同学最多可能有 （ ）
A．1个 B．3个 C．4个 D．5个
第II卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，满分16分，请将正确答案填在答题卡指定位置。
13．圆心为
，且与直线
相切的圆的标准方程为__________。
14．设实数x,y满足约束条件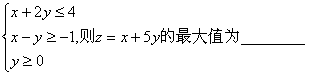
15．将长为4cm，宽为3cm的矩形ABCD，沿对角线AC折成二面角B－AC－D，不论折成的二面角为多少度，A、B、C、D四点始终在同一个球面上，则该球面的表面积=__________cm2。
16．若一系列函数的解析式相同，值域相同，但其定义域不同，则称这一系列函数为“同族函数”。试问解析式为y=x2，值域为{1，2}的“同族函数”共有_______个。
三、解答题：本大题共6小题，满分74分，解答题要在答题卡指定在区域内写出文字说明，演绎推理和逻辑证明。
17．（12分）已知：
通过观察上述两等式的规律，请你写出一般性的命题：
_____________________________________________________= （ * ）
并给出（ * ）式的证明。
18．（12分）已知函数
(a、b、c为常数)的导函数为
，其分别在
处取得极值。
（1）求a、b的值；
（2）解不等式
。
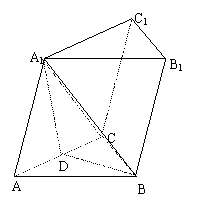
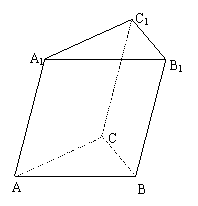19．（12分）如图，在三棱柱ABC－A1B1C1中，△ABC为等边三角形，AB=2，A1A=
，A1B⊥AC，且A1B与平面ABC所成角为60°。
（1）求证：A1C=A1A；
（2）求二面角A1―AC―B的度数。
20．（12分）已知系统M是由6条网线并联而成，且这6条网线能通过的信息量个数分别为1，1，2，2，3，3。在关闭所有网线的情况下，任意接通其中三条网线。
（1）求系统M恰好通过8个信息量的概率。
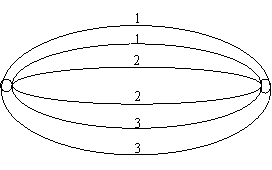（2）若通过的信息量低于6个，系统M就不能保证畅通。试求系统M畅通的概率。
21．（12分）已知抛物线x2=4y的焦点为F，准线为l，过l上任意一点P作抛物线的两条切线，切点分别为A、B。
（1）求证：PA⊥PB；
（2）是否存在常数m，使FA·BF = m PF2恒成立？如果存在，请求出m的值；如果不存在，请说明理由。
22．（14分）已知等差数列{an}满足
（1）求an；
（2）若正项数列{bn}满足
，
求证：
（
）。
数学试题答案
一、选择题（每小题5分，共60分）
1. D 2. A 3. D 4. C 5. D 6. C 7. A 8. C 9. C 10. C 11. D 12.D
二、填空题：每小题4分，共16分
13. (x+1)2+(y―2)2=5 14. 9 15. 25π 16 . 9
三、解答题
17.(12分)
一般形式: 
…………………… 4分
证明 左边 = 
…… 7分
= 
= 
…………………………………………………………… 9分
= 
……… 11分
= 
∴原式得证……………………………………………………………………… 12分
（将一般形式写成 
等均正确，其证明过程可参照给分。）
18．（12分）
（1）∵
∴
……………………………………………………… … 2分
又∵
在处取得极值
∴
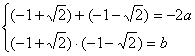……………………………………………… 4分
解得 a = 1，b = ―1……………………………………………………………… 5分
（2）不等式
即 
等价于
……………………………………………………… 7分
即
……………………………………………………… 9分
所以原不等式解集为
………………………… 12分
19．（12分）
（1）取AC中点D，连BD、AD
又∵△ABC为正三解形，∴BD⊥AC……2分
又∵A1B⊥AC，∴AC⊥平面A1BD………4分
而A1D
平面A1BD，∴A1D⊥AC………… 5分
又D为AC中点，∴A1A=AC………………… 6分
（2）由（1）知BD⊥AC，A1D⊥AC
∴∠A1DB为二面角A1―AC―B的平面角………7分
又由（1）知AC⊥平A1BD，AC平面ABC
∴平面A1BD⊥平面ABC
∴∠A1BD为A1B与平面ABC所成角…………………………………………………8分
在△A1DB中，BD=，A1D=
∠A1BD=60°，由正弦定理知
，解得sin∠BA1D= ……………………………10分
又A1D＞BD知∠A1BD＞∠BA1D
∴∠BA1D=30°，故二面角A1―AC―B为90°。 …………………………… 12分
20．（12分）
（1）设系统M恰好通过8个信息量的事件为A，则其概率
……………………………………………………… 5分
（2）设系统M畅通的事件为I，则其概率分别为通过8个信息量（A）、7个信息量（B），6个信息量（C）的和即 P（I）= P（A）+P（B）+P（C）
= 
= 
……………………………………………………
10分
亦可是1减去通过5个信息量（D），4个信息量（E）的概率
即 P（I）= 1－（P（D）+P（E））
= 
= 
………………………………………… 10分
答：系统M恰好通过8个信息量的概率为
,系统M畅通的概率为
. …
12分
21（12分）
（1）∵P点在准线y=－1上，∴设
，
由
从而知
∴
，即
………………………………………
2分
同理可得 
∴x1,x2为方程
∴x1+x2=2a, x1x2 =－4 ……………………………………………………………… 4分
又PA·PB = 
= 
= 
= 
= 0
…………… 6分
∴ PA⊥PB ………………………………………………………………………… 7分
（2）假设存在m使FA·BF =mPF2恒成立
即
恒成立
又
= 
= 
…………………………………………… 10分
∴m=1 …………………………………………………………………………… 12分
22．（14分）
（1）法一：∵数列{an}为等差数列，故可设an=An+ B(A、B为常数)
由
，对n恒成立，得
即
恒成立
∴
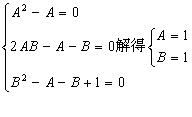
∴an= n+1 ………………………………………………………………………… 6分
法二：设等差数列的公差为d，则
由
得
解得 a1 = 2, d = 1
∴an = n +1 ……………………………………………………………………… 6分
（2）∵bnbn+1=an=n+1,又b1=1
∴ b2 = 2 ………………………………………………………………………… 7分
若n=1，则
…………………………………………………
9分
若
从而有
即 
……………………………………………………………… 11分
∴
= 
= 
= 
（∵
否则b1 = b2 矛盾）……………………………………………… 14分