惠州市一中高三年级数学试卷 (2006 8)
考生须知:
1. 本卷满分150分, 考试时间120分钟.
2. 答题前, 在答题卷密封区内填写班级,姓名和学号.
3. 所有答案必须写在答题卷上, 写在试题卷上无效.
4. 考试结束, 只需上交答题卷.
一:选择题(本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.函数![]() 的反函数是( )
的反函数是( )
A![]() B
B ![]() C
C
![]() D
D ![]()
2 若 f′(x0)=2, 则![]() =( )
=( )
A. -2 B. 2 C. -1 D. 1
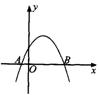 3.如图所示是二次函数
3.如图所示是二次函数![]() 的图像,则
的图像,则![]() 等于( )
等于( )
A.![]() B.
B.![]()
C.![]() D.无法确定
D.无法确定
4.函数y=1+ax(0<a<1)的反函数的图象大致是 ( )
 |
(A) (B) (C) (D)
A B C D
5.函数f(x)=cosx·sinx的图象相邻的两条对称轴之间的距离是( )
A.![]() B.2
B.2![]() C.
C.![]() D.
D.![]()
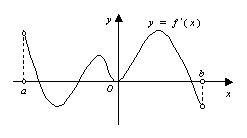 6.函数
6.函数![]() 的定义域为开区间
的定义域为开区间![]() ,导函
数
,导函
数![]() 在
在![]() 内的图象如图所示,则函数
内的图象如图所示,则函数 ![]() 在开区间
在开区间![]() 内有极小值点( )
内有极小值点( )
A.1个
B.2个
C.3个
D.4个
7.如果二次函数y=-2x2+(a-1)x-3,在区间(-∞,![]() 上是增函数,则( )
上是增函数,则( )
A. a=5 B .a=3 C. a≥5 D. a≤-3
8.在等差数列![]() 中,已知
中,已知![]() 则
则![]() 等于 ( )
等于 ( )
A. 40 B. 42 C. 43 D. 45
9.若曲线![]() 的一条切线
的一条切线![]() 与直线
与直线![]() 垂直,则
垂直,则![]() 的方程为( )
的方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.定义集合运算:A⊙B={z︳z= xy(x+y),x∈A,y∈B},设集合A={0,1},B={2,3},则集合A⊙B的所有元素之和为 ( )
A. 0 B. 6 C.12 D.18
二:填空题(本大题共4小题,每小题5分,共20分。把答案填在题中横线上。)
11.函数![]() 的定义域是__________.
的定义域是__________.
12.在等比数列![]() 中,如果a6=6,a9=9, 则a3=__________.
中,如果a6=6,a9=9, 则a3=__________.
13. y=sin2(![]() x)-cos2(
x)-cos2(![]() x)+1的周期是_______________.
x)+1的周期是_______________.
14.关于函数f(x)=lg![]() (x≠0,x∈R)有下列命题:
(x≠0,x∈R)有下列命题:
①函数y=f(x)的图象关于y轴对称。
②当x>0时,f(x)是增函数;当x<0时,f(x)是减函数。
③函数f(x)的最小值是lg2。
④当-1<x<0或x>1时,f(x)是增函数。
⑤f(x)无最大值,也无最小值。
其中正确的命题的序号是________。(注:把你认为正确的命题的序号都填上)
三 解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.)
15.(本小题满分12分)
求下列函数的导数:
y= ex·㏑x
16 (本小题满分12分)
已知函数![]() ,且
,且![]() ,
,![]()
(1) 求a, b的值;
(2)求![]() 的最大值与最小值;
的最大值与最小值;
(3)若![]() ,
,![]() ,且
,且![]() ,求
,求![]() 和值.
和值.
17(本小题满分14分)
已知曲线![]() 和
和![]() 它们交于点P,过P点的两条切线与
它们交于点P,过P点的两条切线与![]() 轴分别交于A,B两点。
轴分别交于A,B两点。
求△ABP的面积。
18 (本小题满分14分)
在等差数列![]() 中,首项
中,首项![]() ,数列
,数列![]() 满足
满足![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)求![]()
19.(本小题满分14分)
已知函数f(x)=x3+ax2+bx+c在x=-![]() 与x=1时都取得极值
与x=1时都取得极值
(1)求a、b的值与函数f(x)的单调区间
(2)若对xÎ〔-1,2〕,不等式f(x)<c2恒成立,求c的取值范围。
20.(本小题满分14分)
设a为实数,记函数![]() 的最大值为g(a)。
的最大值为g(a)。
(1)设t=![]() ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)
(2)求g(a)
(3)试求满足![]() 的所有实数a。
的所有实数a。
惠州市一中高三年级数学试卷参考答案(2006 8)
一. 选择题 :( 本大题共10小题, 每小题5分, 共50分. ) .
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | D | B | A | C | A | C | B | A | D |
二. 填空题: 本大题有4小题, 每小题5分, 共20分.
11 (-∞,2 〕 12 4
13 1 14 ①③④
三. 解答题
15 (本小题满分12分) ∞
解: 由 y= ex·㏑x
得 y′= (ex)′·㏑x+ (ex) ·(㏑x)′
= ex ·㏑x+ ex ·![]()
= ex(㏑x +![]() )
)
16 (本小题满分14分)
解:由题意得: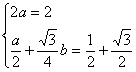 ∴
∴![]()
∴![]()
(2)![]() max=1+
max=1+![]()
![]() min=1-
min=1-![]()
(3)∵![]() ∴
∴![]()
∴![]() 或
或![]()
∴![]() (舍去)或
(舍去)或![]() (K∈Z)
(K∈Z)
 ∴
∴![]()
17(本小题满分14分)
解 : 由![]() 和y=x2得点p的坐标为(1,1)
和y=x2得点p的坐标为(1,1)
又![]() 的导数为y′=-
的导数为y′=-![]() ,则
,则![]() 在P点的导数为-1
在P点的导数为-1
因此![]() 在P点的切线方程为 y-1=-1(x-1)
在P点的切线方程为 y-1=-1(x-1)
即y=-x+2 .
那么点B的坐标为(2,0), 同理A点的坐标为(![]() ,0 ).
,0 ).
∴三角形的面积为SABP=![]() ∣AB∣·h=
∣AB∣·h=![]() ×
×![]() ×1=
×1=![]()
18(本小题满分14分)
解:(1)设等差数列![]() 的公差为d,
的公差为d, ![]() ,
,
![]()
由![]() ,解得d=1.
,解得d=1.
![]()
(2)由(1)得![]()
设![]() ,
,
则![]()
两式相减得![]()

19.(本小题满分14分)
解:(1)f(x)=x3+ax2+bx+c,f¢(x)=3x2+2ax+b
由f¢(![]() )=
)=![]() ,f¢(1)=3+2a+b=0得
,f¢(1)=3+2a+b=0得
a=![]() ,b=-2
,b=-2
f¢(x)=3x2-x-2=(3x+2)(x-1),函数f(x)的单调区间如下表:
| x | (-¥,- | - | (- | 1 | (1,+¥) |
| f¢(x) | + | 0 | - | 0 | + |
| f(x) | | 极大值 | ¯ | 极小值 | |
所以函数f(x)的递增区间是(-¥,-![]() )和(1,+¥)
)和(1,+¥)
递减区间是(-![]() ,1)
,1)
(2)f(x)=x3-![]() x2-2x+c,xÎ〔-1,2〕,当x=-
x2-2x+c,xÎ〔-1,2〕,当x=-![]() 时,f(x)=
时,f(x)=![]() +c
+c
为极大值,而f(2)=2+c,则f(2)=2+c为最大值。
要使f(x)<c2(xÎ〔-1,2〕)恒成立,只需c2>f(2)=2+c
解得c<-1或c>2
20(本小题满分14分)
解:(I)∵![]() ,
,
∴要使![]() 有意义,必须
有意义,必须![]() 且
且![]() ,即
,即![]()
∵![]() ,且
,且![]() ……① ∴
……① ∴![]() 的取值范围是
的取值范围是![]() 。
。
由①得:![]() ,∴
,∴![]()
![]() ,
,![]() 。
。
(II)由题意知![]() 即为函数
即为函数![]()
![]() ,
,![]() 的最大值,
的最大值,
∵直线![]() 是抛物线
是抛物线![]()
![]() 的对称轴,∴可分以下几种情况进行讨论:
的对称轴,∴可分以下几种情况进行讨论:
(1)当![]() 时,函数
时,函数![]() ,
,![]() 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由![]() 知
知![]() 在
在![]() 上单调递增,故
上单调递增,故![]()
![]()
![]() ;
;
(2)当![]() 时,
时,![]() ,
,![]() ,有
,有![]() =2;
=2;
(3)当![]() 时,,函数
时,,函数![]() ,
,![]() 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若![]()
![]() 即
即![]() 时,
时,![]()
![]() ,
,
若![]()
![]() 即
即![]() 时,
时,![]()
![]() ,
,
若![]()
![]() 即
即![]() 时,
时,![]()
![]()
![]() 。
。
综上所述,有![]() =
=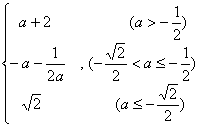 。
。
(III)当![]() 时,
时,![]()
![]()
![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,∴
,∴![]() ,
,
![]()
![]() ,故当
,故当![]() 时,
时,![]()
![]() ;
;
当![]() 时,
时,![]() ,由
,由![]()
![]() 知:
知:![]()
![]() ,故
,故![]() ;
;
当![]() 时,
时,![]() ,故
,故![]() 或
或![]() ,从而有
,从而有![]() 或
或![]() ,
,
要使![]()
![]() ,必须有
,必须有![]() ,
,![]() ,即
,即![]() ,
,
此时,![]()
![]() 。
。
综上所述,满足![]() 的所有实数a为:
的所有实数a为:![]()