2005年高中数学调研卷(12月)
测试时间:120分钟,满分:150分
温馨提示:下列试题中,标有“文科”的文科生做,标有“理科”的理科生做,未标的文科生、理科生都要做。
一、选择题(每题5分,共50分)
1.若集合M=![]() ,N={
,N={![]()
![]() ≤x},则M
≤x},则M![]() N= ( )
N= ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.已知函数![]() 的反函数是
的反函数是![]() ,则 ( )
,则 ( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
3.已知![]() ,且
,且![]() ,那么
,那么![]() 的值是 ( )
的值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.若等差数列{an}只有有限项,且![]() ,前9项的和
,前9项的和![]() 18,前n项和
18,前n项和![]() 240,
240,
则![]() ( )
( )
A.15 B.16 C.17 D.18
5.如果直线L沿x 轴负方向平移6个单位,再沿y轴正方向平移2个单位后,又回到原来的位置,那么直线L的斜率是 ( )
A.3
B.![]() C.
C.![]() D.
D.![]()
6.若a,b都是实数,则![]() 成立的一个充分不必要条件是 ( )
成立的一个充分不必要条件是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.根据条件能得出![]() 为锐角三角形的是 ( )
为锐角三角形的是 ( )
A.![]() B.
B.![]()
C.![]() ,
,![]() ,
,![]() D.
D.![]()
8.(理科)从椭圆![]() 上动点P向圆
上动点P向圆![]() 引切线,则切线长的最小值(
)
引切线,则切线长的最小值(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(文科)中心在原点,准线方程为![]() ,离心率为
,离心率为![]() 的椭圆方程是 ( )
的椭圆方程是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.(理科)一束光线从A![]() 出发,射到直线
出发,射到直线![]() 上B点,经此直线反射后到
上B点,经此直线反射后到![]() 轴上的一点C,若
轴上的一点C,若![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的变化范围是 ( )
的变化范围是 ( )
A.![]() B.
B.![]() C.
C.
![]() D.以上都不对
D.以上都不对
(文科)设![]() ,式中变量
,式中变量![]() 、
、![]() 满足
满足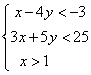 ,则
,则![]() 的变化范围是 ( )
的变化范围是 ( )
A.(6,22) B.(22,32) C.(3,32) D.(3,12)
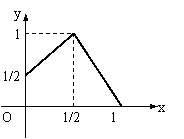 10.设集合M=
10.设集合M=![]() ,f(x)的图象如图,若x0满足x0∈M,
,f(x)的图象如图,若x0满足x0∈M,
且f(f(x0))∈M,则x0的取值范围是 ( )
A.[0,![]() ] B.
] B.![]() C.(
C.(![]() ,
,![]() ) D.
) D.![]()
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.
11.(理科){![]() }是等差数列,
}是等差数列,![]() ,
,![]() ,从{
,从{![]() }中依次取出第2项、第4项、第8项,…,第
}中依次取出第2项、第4项、第8项,…,第![]() 项,按原来的顺序排成一个新数列{
项,按原来的顺序排成一个新数列{![]() },则
},则![]() .
.
(文科)若等差数列![]() 中,
中,![]() ,
,![]() ,
,![]() 成等比数列,则
成等比数列,则![]() .
.
12.直线L:![]() x+y=2
x+y=2![]() 截圆心在原点的圆所得弦长等于圆的半径,则圆的方程是_____
截圆心在原点的圆所得弦长等于圆的半径,则圆的方程是_____
13.(文科)设e1,e2分别为双曲线和它的共轭双曲线的离心率,给出下列结论:
①e12+e22= e12e22 ②e12+e22>4 ③e12+e22< e12e22 ④e12+e22>e12e22
其中正确的序号是_______
(理科)如下关于双曲线离心率的四个命题:
①如果相应于焦点F的准线与实轴相交于N,那么双曲线顶点分![]() 所成的比等于离心率e;
所成的比等于离心率e;
②当双曲线离心率越大时,它的开口就越开阔;③假定两个双曲线有共同渐近线时,则这两个双曲线的离心率相等;④若双曲线的一个焦点到一条渐近线的距离等于实半轴长,则此双曲线的离心率等于![]() ,其中正确命题的序号是______
,其中正确命题的序号是______
14. 设a,b都是正数且![]() ,则
,则![]() 的最大值为____________.
的最大值为____________.
三、解答题:本大题共6小题,共84分.解答应写出文字说明,证明过程或演算步骤.
15.(本小题满分14分)已知-![]() <x<0,sinx+cosx=
<x<0,sinx+cosx=![]() ,
,
(1)求sinx-cosx的值;
(2)求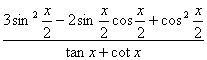 的值
的值
16.(本小题满分14分)
已知A,B,D三点不在同一条直线上,且A(![]() 2,0),B(2,0),
2,0),B(2,0),![]() ,
,
![]() .
.
(1)求点E的轨迹方程;
(2)设过点A的直线l与E点的轨迹相切,与以A,B为焦点的椭圆F相交于M,N两点,且线段MN的中点到y轴的距离为![]() 。求此椭圆F的方程.
。求此椭圆F的方程.
17.(本小题满分14分)在一段笔直的古运河上建有5座拱桥An(n=1,2,3,4,5),经测量知,相邻两座桥之间的距离AnAn+1近似满足 AnAn+1=800+150n(n = 1,2,3,4)米,某公司在每座桥边建有一个货物仓库Bn(n=1,2,3,4,5),其中B1仓库存有货物10吨,B2仓库存有货物20吨,B5仓库存有货物40吨,其他仓库是空的,现在河道上选择一点集中这些仓库的货物,以便于公司对外运输,如果每吨货物水上运输1千米需要0.5元运输费,那么选择哪一点使这批货物的运费最省?
18.(本小题满分14分)
(理科)已知数列{![]() }中,
}中,![]() 是其前n项和,且
是其前n项和,且![]() ,
,![]() =1
=1
(1)若![]() (
(![]() ), 求证{
), 求证{![]() }为等比数列;
}为等比数列;
(2)若![]() (
(![]() ),求证{
),求证{![]() }为等差数列;
}为等差数列;
(3)求数列{![]() }的通项
}的通项![]() .
.
(文科)已知等差数列![]() 中,
中,![]() ,前n项和
,前n项和![]() .
.
(1)求数列![]() 的公差d;
的公差d;
(2)记![]() ,求数列
,求数列![]() 的前n项和为
的前n项和为![]() ;
;
(3)在(2)条件下,是否存在实数M,使得![]() ≤
≤![]() 对一切正整数n都成立?若存在,求出M的最小值.
对一切正整数n都成立?若存在,求出M的最小值.
19.(本小题满分14分)
设双曲线 的两个焦点分别为F1、F2,离心率为2.
(1)若A、B分别为此双曲线的渐近线l1、l2上的动点,且2AB=5 F1F2,求线段AB的中点M的轨迹方程,并说明轨迹是什么曲线;
(2)过点N(1, 0)能否作出直线l,使l交双曲线于P、Q两点,且→OP∙→OQ =0,若存在,求出直线l的方程;若不存在,说明理由.
20.(本题满分14分)
设函数![]() 定义域为R,对任意实数x,y,有
定义域为R,对任意实数x,y,有![]() ,且
,且![]() ,
,![]() .
.
(1)求f(0)
(2)求证:![]() ;
;
(3)求![]() 的周期;
的周期;
(4)(理科)若![]() 时,
时,![]() ,求证:
,求证:![]() 在
在![]() 上单调递减.
上单调递减.
2005年高中数学调研卷(12月)![]() 答卷
答卷
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
![]()
![]()
二、填空题:
11、___________________ 12、________________________
13、___________________ 14、_______________________
三、解答题:
15、
16、
17、
18、
19.
20.
答案(理):
一、DBAAC CDBCC
二、![]() ;
; ![]() ; ②④; 0.5
; ②④; 0.5
三、15、![]()
16、![]() ;
; ![]()
17、B5点;最小费用61元
18、![]() ;
; ![]() ;
; ![]()
19、椭圆![]() ; 不存在
; 不存在
20、(1)1;(3)2π;