广西吴川市川西中学2006届高三向量与立几专题训练
一、 选择题（每题5分）
1、P是△ABC所在平面上一点，若
，则P是△ABC的（ ） A．外心 B．内心 C．重心 D．垂心
2、点O是三角形ABC所在平面内的一点，满足
，则点O是
的（ ）
（A）三个内角的角平分线的交点 （B）三条边的垂直平分线的交点
（C）三条中线的交点 （D）三条高的交点
3、在以下命题中，不正确的命题个数为（ ）
（1）已知A、B、C、D是空间任意四点，则
+
＋
+
＝
；
（2）︱a︱－︱b︱＝︱a＋b︱是a、b共线的充要条件；
（3）若
与
共线，则与所在的直线平行；
（4）对空间任意一点
和不共线的三点A、B、C，若
=
+
+
(其中
)，则
、A、B、C四点共面。
（A） 1个 （B） 2个 （C） 3个 （D） 4个
4、已知向量a＝（1，1，0），b＝（－1，0，2），且
a＋b与2a－b互相垂直，则的值是（ ）（A）1 （B）
（C）
（D）
5、已知a、b、c是空间三非零向量，若︱a－b－c︱＝︱a︱＋︱b︱＋︱c︱,则在下列各结论中，正确的结论为（ ）
（A）a、b、c同向 （B）a与b同向 （C）b、c同向,而a与b反向 （D）a与－(b+c)反向
6、下列命题中，真命题是（ ）
（A）若直线m、n都平行于
，则
（B）设
是直二面角，若直线
则
（C）若m、n在平面内的射影依次是一个点和一条直线，且
，则
或
（D）若直线m、n是异面直线，
，则n与相交
7、设
是两个不重合的平面，m和
是两条不重合的直线，则
的一个充分条件是（ ）
（A）
且
（B）
且
（C）
且
（D）
且
8、有共同底边的等边三角形ABC和BCD所在平面互相垂直，则异面直线AB和CD所成角的余弦值为（ ）
（A）
（B）
（C）
（D）
9、菱形ABCD的边长为
，H分别在AB、BC、CD、DA
上，且
，沿EH与FG把菱形的两个锐角对折起来，使A、C两点重合，这时A点到平面EFGH的距离为（ ）
（A）
（B）
（C）
（D）
10、给出下列命题：
1底面是正多边形的棱锥是正棱锥
2侧棱都相等的棱锥是正棱锥
3侧棱和底面成等角的棱锥是正棱锥
4侧面和底面所成二面角都相等的棱锥是正棱锥
其中正确的命题的个数是（ ）
（A）0 （B）1 （C）2 （D）3
11、长方体三面的面积分别是
，那么它的外接球的半径是（ ）
（A）
（B）
（C）
（D）
12、甲、乙两地都在北纬45
的纬线上，甲地在东经69
，乙地在西经21
，则甲、乙两地在纬度圈上的劣弧长与它们在地球表面的球面距离之比为( )
(A) 3
：4 (B) 
：3
(C) 3：2 (D) ：
13、“平面内不共线的三点到平面
的距离相等”是“∥”的………（ ）
（A）充要条件 （B）充分不必要条件
（C）必要不充分条件 （D）既不充分也不必要条件
14、 已知一个简单多面体的各个面都是三角形，则顶点数V与面数F满足的关系是( )
A.2V+F=4 B.2V－F=4 C.2V+F=2 D.2V－F=2
二、 填空题（每题5分）
15、已知a＝（5，4），b＝（3，2），则与2a－3b平行的单位向量为________。
16、已知平面上三点A、B、C满足
＝3, 
＝4, 
＝5,则
的值等于__________。
17、已知向量
，且A、B、C三点共线，则k=
18、若非零向量α、β满足α+β=α－β，则α与β所成角的大小为_____.
二、解答题：
19、（本大题满分14分）已知a=（cosα，sinα）,b=（cosβ,sinβ）(0<α<β<π)，
（1）求证： a+b与a-b互相垂直；
（2）若ka+b与a-kb的大小相等(k∈R且k≠0)，求β－α
20、（本大题满分12分）
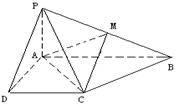已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，
底面ABCD，且PA=AD=DC=
AB=1，M是PB的中点。
（Ⅰ）证明：面PAD⊥面PCD；
（Ⅱ）求AC与PB所成的角；
（Ⅲ）求面AMC与面BMC所成二面角的大小。
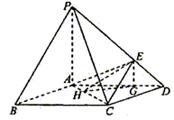
21、（本小题满分12分）如图，在底面是菱形的四棱锥P—ABCＤ中，
∠ABC=600，PA=AC=a，PB=PD=
,点E在PD上，且PE:ED=2:1.
（1）证明PA⊥平面ABCD；
（2）求以AC为棱，EAC与DAC为面的二面角
的大小；
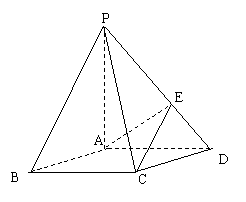（3）在棱PC上是否存在一点F，使BF//平面AEC？证明你的结论.
22、（本小题满分12分）平面直角坐标系中，O为坐标原点，给定两点A（1，0）、B（0，
－2），点C满足
、
（1）求点C的轨迹方程；
（2）设点C的轨迹与双曲线
交于两点M、N，且以MN为直径的圆过原点，求证：
.
向量与立几专题训练参考答案
一、选择题：
1-5：DBCDC 6-10：CCBAA 11-14：AACC
二、填空题：
15、
16、 -25 17、
18、
三、解答题
19、（1）证法一：∵a=（cosα，sinα）,b=（cosβ,sinβ）
∴a+b＝（cosα+cosβ，sinα+ sinβ）, a-b＝（cosα-cosβ，sinα- sinβ）
∴(a+b)·(a-b)=（cosα+cosβ，sinα+ sinβ）·（cosα-cosβ，sinα- sinβ）
=cos2α-cos2β+sin2α- sin2β=0
∴(a+b)⊥(a-b)
证法二：∵a=（cosα，sinα）,b=（cosβ,sinβ） ∴a＝1，b＝1
∴(a+b)·(a-b)= a2-b2=a2-b2=0 ∴(a+b)⊥(a-b)
证法三：∵a=（cosα，sinα）,b=（cosβ,sinβ）∴a＝1，b＝1,
记
＝a，
＝b，则＝=1,
又α≠β，∴O、A、B三点不共线。
由向量加、减法的几何意义，可知以OA、OB为邻边的平行四边形OACB是菱形，其中
＝a+b，
＝a-b，由菱形对角线互相垂直，知(a+b)⊥(a-b)
（2）解：由已知得ka+b与a-kb,
又∵ka+b2＝(kcosα+cosβ)2+(ksinα+sinβ)2=k2+1+2kcos(β－α),
ka+b2＝(cosα-kcosβ)2+(sinα-ksinβ)2=k2+1-2kcos(β－α),
∴2kcos(β－α)= -2kcos(β－α)
又∵k≠0 ∴cos(β－α)＝0
∵0<α<β<π ∴0<β－α<π, ∴β－α=
注：本题是以平面向量的知识为平台，考查了三角函数的有关运算，同时也体现了向量垂直问题的多种证明方法，常用的方法有三种，一是根据数量积的定义证明，二是利用数量积的坐标运算来证明，三是利用向量运算的几何意义来证明。
20、本小题主要考查直线与平面垂直、直线与平面所成角的有关知识及思维能力和空间想象能力.考查应用向量知识解决数学问题的能力.满分12分.
|
（Ⅰ）证明：∵PA⊥面ABCD，CD⊥AD，
∴由三垂线定理得：CD⊥PD.
因而，CD与面PAD内两条相交直线AD，PD都垂直，
∴CD⊥面PAD.
又CD
面PCD，∴面PAD⊥面PCD.
（Ⅱ）解：过点B作BE//CA，且BE=CA，
则∠PBE是AC与PB所成的角.
连结AE，可知AC=CB=BE=AE=，又AB=2，
所以四边形ACBE为正方形. 由PA⊥面ABCD得∠PEB=90°
在Rt△PEB中BE=，PB=
， 
（Ⅲ）解：作AN⊥CM，垂足为N，连结BN.
在Rt△PAB中，AM=MB，又AC=CB，
∴△AMC≌△BMC,
∴BN⊥CM，故∠ANB为所求二面角的平面角.
∵CB⊥AC，由三垂线定理，得CB⊥PC，
在Rt△PCB中，CM=MB，所以CM=AM.
在等腰三角形AMC中，AN·MC=
，
. ∴AB=2，
故所求的二面角为
|
所以AB=AD=AC=a， 在△PAB中，
由PA2+AB2=2a2=PB2 知PA⊥AB.
同理，PA⊥AD，所以PA⊥平面ABCD…………3分
（Ⅱ）解 作EG//PA交AD于G，
由PA⊥平面ABCD.
知EG⊥平面ABCD.作GH⊥AC于H，连结EH，则EH⊥AC，∠EHG即为二面角的平面角.
又PE : ED=2 : 1，所以
从而
……………7分
（Ⅲ） 当F是棱PC的中点时，BF//平面AEC，证明如下，
证法一 取PE的中点M，连结FM，则FM//CE. ①
由 
知E是MD的中点.
连结BM、BD，设BD
AC=O，则O为BD的中点.
所以 BM//OE. ②
由①、②知，平面BFM//平面AEC.
又 BF平面BFM，所以BF//平面AEC.
证法二因为 
所以 
、
、
共面.
又 BF
平面ABC，从而BF//平面AEC.
22、解答：（1）解：设
即点C的轨迹方程为x+y=1 ……4分
