海门市锡类中学二轮专题立体几何同步练习
生化 姓名 学号
一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．给出下列命题：
①有一条侧棱与底面两边垂直的棱柱是直棱柱；
②底面为正多边形的棱柱为正棱柱；
③顶点在底面上的射影到底面各顶点的距离相等的棱维是正棱锥；
④A、B为球面上相异的两点，则通过A、B的大圆有且公有一个。
其中正确命题的个数是 （ ）
A．0个 B．1个 C．2个 D．3个
2．不共面的四个定点到平面
的距离都相等，这样的平面共有
（ ）
A．3个 B．4个 C．6个 D．7个
3．一个与球心距离为1的平面截球所得的圆面面积为
，则球的表面积为 （ ）
A．
B．
C．
D．
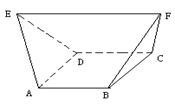4．如图，在多面体ABCDEF中，已知ABCD是边长为1的正方形，且△ADE、△BCF均为正三角形，EF∥AB，EF＝2，则该多面体的体积为
（ ）
A．
B．
C．
D．
5．设α、β、γ为平面，
为直线，则
的一个充分条件是 （ ）
A．
B．
C．
D．
6．如图，正方体ABCD－A1B1C1D1的棱长为1，O是底面A1B1C1D1的中心，则O到平面ABC1D1的距离为 （ ）
A．
B．
C． D．
7．平面P与平面Q所成的二面角为
，直线AB
平面P，且与二面角棱成
角，它与平面Q成
角，那么
（ ）
A. 
B. 
C. 
D. 
8．正方体ABCD－A1B1C1D1中，E、F分别为棱AB、C1D1的中点，则直线A1B1与平面A1ECF所成角的正弦为 （ ）
A． B． C． D．
9．长方体的一个顶点上三条棱的长分别为a、b、c，若长方体所有棱的长度之和为24，一条对角线长度为5，体积 为2，则
等于
（ ）
A. 
B. 
C. 
D
10．若三棱锥A-BCD的侧面ABC内一动点P到底面BCD的距离与到棱AB的距离相等，则动点P的轨迹与△ABC组成图形可能是 （ ）
A. B. C. D.
11．过三棱柱任意两个顶点的直线共15条，其中异面直线有 （ ）
A．18对 B．24对 C．30对 D．36对
12．将半径都为1的4个钢球完全装入形状为正四面体的容器里，这个正四面体的高的最小值为 （ ）
A．
B．2＋
C．4＋ D．
海门市锡类中学二轮专题立体几何同步练习
生化 姓名 学号
答题纸
一、选择题：本大题共12小题，每小题5分，共60分．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题：本大题共5小题，每小题4分，共24分．把答案填在横线上．
13．正三棱锥P－ABC的四个顶点同在一个半径为2的球面上，若正三
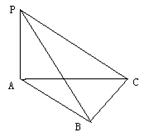棱锥的侧棱长为2，则正三棱锥的底面边长是_____________ ．
14．如图，PA⊥平面ABC，∠ABC＝90°且PA＝AB＝BC＝a，
则异面直线PB与AC所成角的正切值等于______．
15．已知球面上A、B两点间的球面距离是1，过这两点的球面半径的
夹角为60°，则这个球的表面积与球的体积之比是
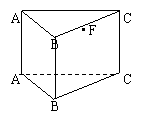16．如图，在直三棱柱
中，
，
，
，E、F分别为
的中点，沿棱柱的表面从E到F两点的最短路径的长度为
。
17．下面是关于三棱锥的四个命题：
①底面是等边三角形，侧面与底面所成的二面角都相等的三棱锥是正三棱锥．
②底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥．
③底面是等边三角形，侧面的面积都相等的三棱锥是正三棱锥．
④侧棱与底面所成的角都相等，且侧面与底面所成的二面角都相等的三棱锥是正三棱锥．
其中，真命题的编号是______________（写出所有真命题的编号）．
18．正方体ABCD－A1B1C1D1中，过对角线BD1的一个平面交AA1于E，交CC1于F，则： ① 四边形BFD1E一定是平行四边形 ；② 四边形BFD1E有可能是正方形；③四边形BFD1E在底面ABCD内的投影一定是正方形；④ 四边形BFD1E有可能垂直于平面BB1D。以上结论正确的为 （写出所有正确结论的编号）．
三、解答题：本大题共5小题，共66分．解答应写出文字说明，证明过程或演算步骤．
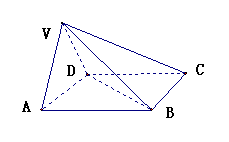19．(本题满分l2分) 在四棱锥V－ABCD中，底面ABCD是正方形，侧面VAD是正三角形，平面VAD⊥底面ABCD．
（Ⅰ）证明AB⊥平面VAD．
（Ⅱ）求面VAD与面VDB所成的二面角的大小．
20．（本题满分12分）如图1，已知ABCD是上、下底边长分别是2和6，高为的等腰梯形．将它沿对称轴OO1折成直二面角，如图2．
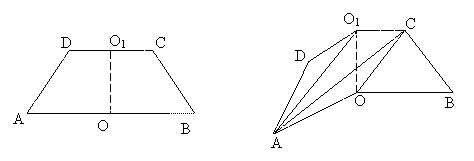
（Ⅰ）证明AC⊥BO1；
（Ⅱ）求二面角O－AC－O1的大小．
21．（本题满分14分）
如图，在底面是矩形的四棱锥P—ABCD中，PA⊥底面ABCD，PA＝AB＝1，BC＝2．
（1）求证：平面PDC⊥平面PAD；
（2）若E是PD的中点，求异面直线AE与PC所成角的余弦值；
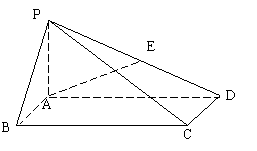（3）在BC边上是否存在一点G，使得D点到平面PAG的距离为1，若存在，求出BG的值；若不存在，请说明理由．
22．（本题满分14分）
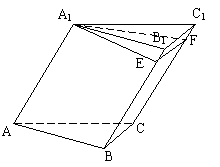
如图，已知三棱柱ABC－A1B1C1的底面是边长为2的正三角形，侧棱A1A与AB、AC均成45°角，且A1E⊥B1B于E，A1F⊥CC1于F．
⑴求证：平面A1EF⊥平面B1BCC1；
⑵求直线AA1到平面B1BCC1的距离；
⑶当AA1多长时，点A1到平面ABC与平面B1BCC1的距离相等．
 |
23．(本题满分14分) 如图，甲、乙是边长为4a的两块正方形钢块，现在将甲裁剪焊接成一个正四棱柱，将乙裁剪焊接成一个正四棱锥，使它们的全面积等于一个正方形的面积（不计焊接缝的面积）
（1）将你的裁剪方法用虚线标示在图中，并作简要的说明；
（2）试比较你所制作的正四棱柱与正四棱锥体积的大小，并证明你的结论。
 |
海门市锡类中学二轮专题立体几何同步练习
参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | D | D | A | B | B | A | A | A | D | D | C |
二、填空题
13．3； 14．； 15．π； 16． 
17．①③④ 18．①③④
三、解答题
19．证明：（Ⅰ）作AD的中点O，则VO⊥底面ABCD．…………………………1分
建立如图空间直角坐标系，并设正方形边长为1，………………2分
则A（
，0，0），B（，1，0），C（－，1，0），
D（－，0，0），V（0，0，
），
∴
……………………3分
由
………………………4分
…………………5分
又AB∩AV＝A
∴AB⊥平面VAD…………………………………………6分
（Ⅱ）由（Ⅰ）得
是面VAD的法向量………………………7分
设
是面VDB的法向量，则
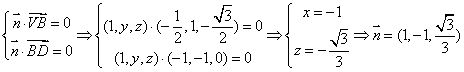9分
∴
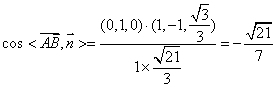，………………………………11分
又由题意知，面VAD与面VDB所成的二面角，所以其大小为
……12分
20．解法一
（I）证明 由题设知OA⊥OO1，OB⊥OO1.
所以∠AOB是所折成的直二面角的平面角，
即OA⊥OB. 故可以O为原点，OA、OB、OO1
所在直线分别为
轴、y轴、z轴建立空间直角坐标系，
如图3，则相关各点的坐标是A（3，0，0），
B（0，3，0），C（0，1，
）
|
）.
从而
所以AC⊥BO1.
（II）解：因为
所以BO1⊥OC，
由（I）AC⊥BO1，所以BO1⊥平面OAC，
是平面OAC的一个法向量.
设
是0平面O1AC的一个法向量，
由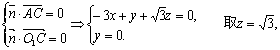
得
.
设二面角O—AC—O1的大小为
，由
、的方向可知
，>，
所以cos
，>=
即二面角O—AC—O1的大小是
解法二
（I）证明 由题设知OA⊥OO1，OB⊥OO1，所以∠AOB是所折成的直二面角的平面角，
即OA⊥OB. 从而AO⊥平面OBCO1，
OC是AC在面OBCO1内的射影.
因为
，
所以∠OO1B=60°，∠O1OC=30°，从而OC⊥BO1
由三垂线定理得AC⊥BO1.
（II）解 由（I）AC⊥BO1，OC⊥BO1，知BO1⊥平面AOC.
设OC∩O1B=E，过点E作EF⊥AC于F，连结O1F（如图4），
则EF是O1F在平面AOC内的射影，由三垂线定理得O1F⊥AC.
所以∠O1FE是二面角O—AC—O1的平面角.
由题设知OA=3，OO1=，O1C=1，
所以
，
从而
， 又O1E=OO1·sin30°=
，
所以
即二面角O—AC—O1的大小是
21．解：以A为原点，AB所在直线为x轴，AD所在直线为x轴、y轴，AP所在直线为z轴建立空间直角坐标系，
则A(0，0，0)，B(1，0，0)，C(12，0，)，D(0，2，0)，E(0，1，)，P(0，0，1)．
∴
＝(－1，0，0)，
＝(0，2，0)，
＝(0，0，1)，
＝(0，1，) ，
＝(1，2，－1)，
(1) 
平面PDC⊥平面PAD……5分
(2)∵cos
＝＝，
∴所求角的余弦值为．………………………………………………………………9分
(3)假设BC边上存在一点G满足题设条件，令BG＝x，则G(1，x，0)，作DQ⊥AG，则DQ⊥平面PAG，即DQ＝1．∵2S△ADG＝S矩形ABCD，
∴
＝2∴
＝2，又AG＝，∴x＝<2，
故存在点G，当BG＝时，使点D到平面PAG的距离为1．…………………………14分
22．解：⑴CC1∥BB1，又BB1⊥A1E，∴CC1⊥A1E，而CC1⊥A1F，∴CC1⊥平面A1EF，∴平面A1EF⊥平面B1BCC1………………………………………………………4分
⑵作A1H⊥EF于H，则A1H⊥面B1BCC1，∴A1H为A1到面B1BCC1的距离，在△A1EF中，A1E＝A1F＝，EF＝2，∴△A1EF为等腰Rt△且EF为斜边，∴A1H为斜边上中线，可得A1H＝EF＝1……………………………………………………9分
⑶作A1G⊥面ABC于G，连AG，则A1G就是A1到面ABC的距离，且AG是∠BAC的角平分线，A1G＝1……………………………………………………………12分
∵cos∠A1AG＝，∴sin∠A1AG＝，∴A1A＝＝1………………14分
23．（1）将正方形甲按图中虚线剪开，以两个正方形为底面，四个长方形为侧面，焊接成一个底面边长为2a，高为a的正四棱柱。将正方形乙按图中虚线剪开，以两个长方形焊接成边长为2a的正方形为底面，三个等腰三角形为侧面，两个直角三角形合拼成为一个侧面，焊接成一个底面边长为2a，斜高为3a的正四棱锥。
 |  |
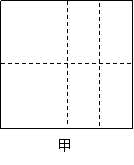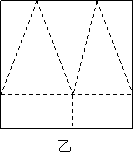（2）∵正四棱柱的底面边长为2a，高为a，∴其体积为V柱=
，
又∵正四棱锥的底面边长为2a，高长=
，
∴其体积为V锥=
，
，即
，
，即V柱>V锥
故所制作的正四棱柱的体积比正四棱锥的体积大。