高三总复习单元测试题 ___函数
1、点(x, y)在映射“f”的作用下的象是点(x+2y, 3x-4y),则在此映射的作用下的点(5, 6)的原象是( )。
A (5, 6) B (17, -9) C (![]() ,
, ![]() )
D 其它答案
)
D 其它答案
2、1、下列四组函数中,表示同一函数的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3、已知一个二次函数的对称轴为x=2,它的图象经过点(2, 3),且与某一次函数的图象交于点(0, -1),那么已知的二次函数的解析式是( )。
A . f (x)=-x2-4x-1 B. f (x)=-x2+4x+1
C. f (x)=-x2+4x-1 D. f (x)=x2-4x+1
4、函数f (x)=4x2-mx+5,当x∈(-2, +∞)时是增函数,当x∈(-∞, -2)时是减函数,则f (1)的值是( )。
A -7 B 25 C 1 7 D 1
5、设f (x)是定义在R上最小正周期为T的函数,则f (2x+3)是( )。
A 最小正周期为T 的函数 B 最小正周期为2T的函数
C 最小正周期为![]() 的函数
D 不是周期函数
的函数
D 不是周期函数
6、奇函数y=f (x)的反函数是y=f -1(x),函数y=f -1(x)在x∈[0, +∞)上是减函数,则函数y=-f (x)在x∈(-∞, 0)上是( )。
A 增函数 B 减函数 C 不是单调函数 D 常值函数
7、函数![]() 的反函数
的反函数![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、函数![]() 的图象必不过( )
的图象必不过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9、已知函数![]() ,那么( )
,那么( )
A.![]() 是减函数
B.
是减函数
B.![]() 在
在![]() 上是减函数
上是减函数
C.![]() 是增函数
D.
是增函数
D.![]() 在
在![]() 上是增函数
上是增函数
10、如果奇函数![]() 在
在![]() 上是增函数且最小值是5,那么
上是增函数且最小值是5,那么![]() 在
在![]() 上是( )
上是( )
A.增函数且最小值是![]() B增函数且最大值是
B增函数且最大值是![]() .
.
C.减函数且最小值是![]() D.减函数且最大值是
D.减函数且最大值是![]()
11、下列各图象表示的函数中,存在反函数的只能是( )
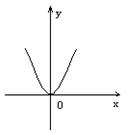 A. B
A. B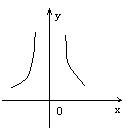 .
. 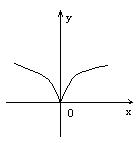 C.
C. 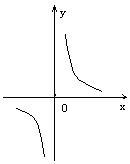 D.
D.
12、已知c>0, 在下列不等式中成立的一个是( )。
A c>2c B c>(![]() )c C 2c<(
)c C 2c<(![]() )c D 2c>(
)c D 2c>(![]() )c
)c
二、填空题
13、函数![]() 在
在![]() 上的最大值与最小值之和为
上的最大值与最小值之和为
14、![]() 在R上为减函数,则
在R上为减函数,则![]()
15、函数y=x+![]() 在区间[2, 5]上的最大值为____________
在区间[2, 5]上的最大值为____________
16、已知关于x的方程x2+2ax+2a2-10=0有一个根大于2,另一个根小于2,则a的取值范围是 .
三、解答题
17、设![]() 是奇函数,
是奇函数,![]() 是偶函数,并且
是偶函数,并且![]() ,求
,求![]() 。
。
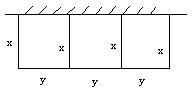
18、有一批材料可以建成长为![]() 的围墙,如果用材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图),则围成的矩形的最大面积是多少?
的围墙,如果用材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如图),则围成的矩形的最大面积是多少?
19、已知函数![]() ,
,![]() (
(![]() 为正常数),且函数
为正常数),且函数![]() 与
与![]() 的图象在
的图象在![]() 轴上的截距相等。
轴上的截距相等。
⑴求![]() 的值;
的值;
⑵求函数![]() 的单调递增区间。
的单调递增区间。
20、设函数f(x)的定义域是R,对于任意实数m,n,恒有f(m+n)=f(m)f(n),且当x>0时,0<f(x)<1。
⑴求证:f(0)=1,且当x<0时,有f(x)>1;
⑵判断f(x)在R上的单调性;
⑶设集合A={(x,y)f(x2)f(y2)>f(1)},集合B={(x,y)f(ax-y+2)=1,a∈R},若A∩B=![]() ,求a的取值范围。
,求a的取值范围。
高三总复习单元测试题答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | D | C | B | C | A | B | A | D | B | D | C |
二、填空题
13、 3
14、 (
![]() ,1) 15、
,1) 15、![]() 16、( – 1 ,1)
16、( – 1 ,1)
17、![]() 为奇函数
为奇函数 ![]()
![]() 为偶函数
为偶函数 ![]()
![]()
从而 ![]()
![]()
18、设每个小矩形长为x,宽为y,则
![]()
![]()
19、解:⑴由题意,![]() ,
,![]() 又
又![]() ,所以
,所以![]() 。
。
⑵![]()
当![]() 时,
时,![]() ,它在
,它在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,它在
,它在![]() 上单调递增。
上单调递增。
20、解:⑴f(m+n)=f(m)f(n),令m=1,n=0,则f(1)=f(1)f(0),且由x>0时,0<f(x)<1,∴f(0)=1;设m=x<0,n=-x>0,∴f(0)=f(x)f(-x),∴f(x)=![]() >1。
>1。
⑵设x1<x2,则x2-x1>0,∴0<f(x2-x1)<1,∴f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)=f(x2-x1)f(x1)-f(x1)=f(x1)[f(x2-x1)-1]<0,∴f(x)在R上单调递减。
⑶∵f(x2)f(y2)>f(1),∴f(x2+y2)>f(1),由f(x)单调性知x2+y2<1,又f(ax-y+2)=1=f(0),
∴ax-y+2=0,又A∩B=![]() ,∴
,∴![]() ,∴a2+1≤4,从而
,∴a2+1≤4,从而![]() 。
。