中档题训练(七)函数部分1
1. 设关于![]() 的二次方程
的二次方程![]() 的两根
的两根![]() 满足
满足![]() ,求
,求![]() 的取值范围.
的取值范围.
2. 在函数![]() 的图象上有A、B两动点,满足AB∥x轴,点M(1,m)(m为常数,m>3)是三角形ABC的边BC的中点,设A点横坐标t,△ABC的面积为f (t).
的图象上有A、B两动点,满足AB∥x轴,点M(1,m)(m为常数,m>3)是三角形ABC的边BC的中点,设A点横坐标t,△ABC的面积为f (t).
(1) 求f (t)的解析表达式;
(2) 若f (t)在定义域内为增函数,试求m的取值范围;
(3) 是否存在m使函数f (t)的最大值18?若存在,试求出m的值;若不存在,请说明理由。
3. 已知![]() ,求
,求![]() 的解析式。
的解析式。
4. 命题p:函数![]() 的定义域为
的定义域为![]() ;命题q:不等式
;命题q:不等式![]() 对一切正实数均成立.如果命题p或q为真命题,命题p且q为假命题,求实数a的取值范围.
对一切正实数均成立.如果命题p或q为真命题,命题p且q为假命题,求实数a的取值范围.
5. 已知函数![]() (1)证明:函数
(1)证明:函数![]() 在
在![]() 上为增函数;
上为增函数;
(2)用反证法证明方程![]() 没有负数根.
没有负数根.
6. 已知![]()
![]() ,(1)若
,(1)若![]() ,求
,求![]() 的最小值;(2)若不等式
的最小值;(2)若不等式![]() 对于一切
对于一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
7. 已知二次函数f(x)=a![]() (a>0),对称轴方程为
(a>0),对称轴方程为![]()
![]() ,方程f(x)=1有一个根为0,方程f(x)=x有两个根
,方程f(x)=1有一个根为0,方程f(x)=x有两个根![]() ,
,![]() .⑴如
.⑴如![]() <2<
<2<![]() <4 .求证:
<4 .求证: ![]() >-1.
>-1.
⑵如0<![]() <2 ,
<2 ,![]() -
-![]() =2 .求b的取值范围.
=2 .求b的取值范围.
中档题训练(八)函数部分2
1. 已知二次函数![]() (
(![]()
![]() R,
R,![]()
![]() 0).
0).
(I)当0<![]() <
<![]() 时,
时,![]() (
(![]()
![]() R)的最大值为
R)的最大值为![]() ,求
,求![]() 的最小值.
的最小值.
(II)如果![]() [0,1]时,总有
[0,1]时,总有![]()
![]() .试求
.试求![]() 的取值范围.
的取值范围.
(III)令![]() ,当
,当![]() 时,
时,![]() 的所有整数值的个数为
的所有整数值的个数为![]() ,求证数列
,求证数列![]() 的前
的前![]() 项的和
项的和![]() .
.
2. 若不等式![]()
![]() 对任意的实数x均成立,求实数a的取值范围。
对任意的实数x均成立,求实数a的取值范围。
3. 已知函数![]() (k为正实数,
(k为正实数,![]() )定义域为
)定义域为![]() ,问:是否存在实数a,b使得当
,问:是否存在实数a,b使得当![]() 时,f(x)的值可取到一切正数,且
时,f(x)的值可取到一切正数,且![]() 若存在,求出a、b的值,若不存在,请说明理由。
若存在,求出a、b的值,若不存在,请说明理由。
4.设集合![]() 若A∩B≠
若A∩B≠![]() ,求m的取值范围。
,求m的取值范围。
5. 已知![]() ,
,![]() ,求
,求![]() 的最大值与最小值。
的最大值与最小值。
6.. 若不等式![]() 对任意的实数
对任意的实数![]() 均成立,求实数
均成立,求实数![]() 的取值范围。
的取值范围。
7.. 设定义在[-2,2]上的偶函数f(x)在区间[0,2]上单调递减,若f(1-m)<f(m),求实数m的取值范围。
中档题强化训练(九)函数部分3
1. (1)已知函数y=f(x)的定义域为R,且当x∈R时,f(m+x)=f(m-x)恒成立,求证:y=f(x)的图象关于直线x=m对称。(2)若函数y=log2ax-1的图象的对称轴是x=2,求非零实数a的值。
2. 已知函数f(x)=lg[(a2-1)x2+(a+1)x+1],(1)若f(x)的定义域为(-∞,+∞),求实数a的取值范围;(2)若f(x)的值域为(-∞,+∞),求实数a的取值范围。
3.是否存在实数a,使得f(x)=loga(ax-![]() 在区间[2,4]上是增函数?若存在,求出a的取值范围;若不存在,说明理由。
在区间[2,4]上是增函数?若存在,求出a的取值范围;若不存在,说明理由。
4. 已知函数f(x)=log3x+2,x∈[1,9],求函数y=[f(x)]2+f(x2)的最大值。
5. 设![]() .⑴求
.⑴求![]() 的定义域
的定义域
⑵ ![]() 是否存在最大值或最小值
是否存在最大值或最小值
6.已知函数![]() 。⑴当
。⑴当![]() 时,求
时,求![]() 的最大值和最小值;⑵求
的最大值和最小值;⑵求![]() 的范围,使
的范围,使![]() 在区间
在区间![]() 上是单调函数。
上是单调函数。
7 已知函数![]() ,问是否存在实数
,问是否存在实数![]() ,使
,使![]() 在[-1,2]上取得最大值3,最小值-29,若存在,求出
在[-1,2]上取得最大值3,最小值-29,若存在,求出![]() 的值,并指出函数的单调区间,若不存在,请说明理由。
的值,并指出函数的单调区间,若不存在,请说明理由。
中档题训练(七)参考答案
1.解:设![]()
![]() 方程
方程![]() 的两个根
的两个根![]() 满足
满足![]()
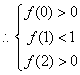
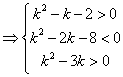 解之得:
解之得:![]()
![]()
2.解:(1) f (t) = 2t (m-3t2) ![]()
(2) ![]()
![]() ∵
∵![]() 上是增函数.
上是增函数.
∴![]()
![]() 即
即![]() 上恒成立.
上恒成立.
![]() 即m的取值范围
即m的取值范围![]()
(3) 令f’(t)=0,得![]() (其中
(其中![]() 舍去)
舍去) ![]() 即
即![]() 时,在
时,在![]() 处
处 ![]() =12,此时m的值不存在.
=12,此时m的值不存在.
令![]() ,即m>9由(2)知f (t)在
,即m>9由(2)知f (t)在 ![]() 为增函数,
为增函数,![]() ,由2(m-3)=18得m=12 综上只存在m=12适合题意。
,由2(m-3)=18得m=12 综上只存在m=12适合题意。
3. 解:令![]()
则![]()
![]()
![]() 的解析式为
的解析式为![]()
说明:此题极易忽略![]() 的定义域,换元时要注意中间变量的取值范围。
的定义域,换元时要注意中间变量的取值范围。
4.解: 命题p为真命题![]() 函数
函数![]() 的定义域为R
的定义域为R![]()
![]() 对任意的x均成立
对任意的x均成立![]() 时,-x>0解集为
时,-x>0解集为![]() ;或者
;或者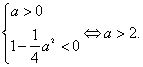 命题q为真命题
命题q为真命题![]()
![]() 对一切正实数均成立
对一切正实数均成立
![]() 对一切正实数均成立.
对一切正实数均成立.
![]()
所以,命题q为真命题a≥1
根据题意知,命题p与q为有且只有一个为真命题. 当命题p为真命题且命题q为假命题时a不存在;当命题q为真命题且命题p为假命题时a的取值范围是[1,2].综上,命题p或q为真命题,命题p且q为假命题,实数a的取值范围是[1,2].
5.解:(1)设![]()
![]()
![]() ∴
∴![]() 在
在![]() 上为增函数
上为增函数
(2)假设![]() 有负根
有负根![]() ,则有
,则有![]() 即
即![]() 显然
显然![]() 当
当![]()
而![]() ,这是不可能的,即不存在
,这是不可能的,即不存在![]() 的解.
的解.
当![]() 矛盾,即不存在
矛盾,即不存在![]() 的解.
的解.
综上,假设不成立,即不存在负根.
6.(1)![]()
![]() ,
,
∴![]() ,等号当且仅当
,等号当且仅当![]() ,即
,即![]() 时取得。∴
时取得。∴![]() 的最小值为
的最小值为![]() 。
。
(2)不等式即为![]() ,也就是
,也就是![]() ,
,
令![]() ,则
,则![]() 在
在![]() 上恒成立,∴
上恒成立,∴![]() ,解得
,解得![]() 。
。
7.解:⑴![]() 有根为0
有根为0![]() ,设
,设![]()
![]()
![]()
![]()
![]() 。
。
⑵![]() 由⑴
由⑴![]() 又
又![]()
![]() 。
。
中档题训练(八)参考答案
1.解:⑴由![]() 知
知![]() 故当
故当![]() 时
时![]() 取得最大值为
取得最大值为![]() ,即
,即![]() ,所以
,所以![]() 的最小值为
的最小值为![]() ;
;
⑵由![]() 得
得![]()
![]() 对于任意
对于任意![]() 恒成立,
恒成立,
当![]() 时,
时,![]() 使
使![]() 成立;
成立;
|
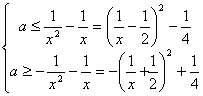 对于任意的
对于任意的⑶当![]() 时,
时,![]() ,则此二次函数的对称轴为
,则此二次函数的对称轴为![]() ,开口向上,故
,开口向上,故![]() 在
在![]() 上为单调递增函数,且当
上为单调递增函数,且当![]() 时,
时,![]() 均为整数,故
均为整数,故![]() ,则数列
,则数列![]() 的通项公式为
的通项公式为![]() ,故
,故![]() ①,又
①,又![]() ②,
由①—②得
②,
由①—②得
![]() ,
,![]() 。
。
2.解:设![]() 故原题条件可等价转化为:
故原题条件可等价转化为:![]() 在
在![]() 上恒为正值。以a为参数,则有
上恒为正值。以a为参数,则有 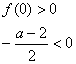 或
或![]() 即
即 ![]() 或
或![]() ,解得2<a<5或
,解得2<a<5或![]()
3.解:假设存在满足条件的实数a,b,由![]() 。
。![]()
![]()
![]() 1
1
又![]() 2由1、2可解得
2由1、2可解得![]() 。
。
4.答案:![]()
5.解: ![]()
![]()
![]()
![]()
![]()
![]()
![]() =
=![]() =
=![]()
![]()
6.解:令![]()
![]() 对任意的实数
对任意的实数![]() 均成立
均成立
令![]()

7.解:∵f(x)是偶函数,∴f(1-m)=f(1-m),f(m)=f(m),
于是f(1-m)<f(m)![]() f(1-m)<f(m),
f(1-m)<f(m),
∵f(x)在[0,2]上是减函数,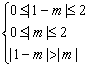 ,解之得:-1≤m<
,解之得:-1≤m<![]()
中档题训练(九)参考答案
1.解:(1)设P(x0,y0)是y=f(x)图象上任一点,则y0=f(x0),点P关于直线x=m的对称点为P',则P'的坐标为(2m-x0,y0),因为f(2m-x0)=f[m+(m-x0)]=f[m-(m-x0)]=f(x0)=y0,即P'(2m-x1,y0)在y=f(x)的图象上,故y=f(x)的图象关于直线x=m对称。
(2)由(1)知f(2-x)=f(2+x)恒成立,∴a(2-x)-1=a(2+x)-1恒成立,即-ax+(2a-1)=ax+(2a-1),又∵a≠0,∴2a-1=0,得a=![]() 。
。
2.解:(1)据题意,(a2-1)x2+(a+1)x+1>0对一切x∈R恒成立
当a2-1≠0时,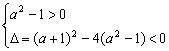 解之得:a<-1或a>
解之得:a<-1或a>![]()
当a2-1=0时,若a=1,f(x)=lg(2x+1),不合题意,当a=-1时,f(x)=0,符合题意,综上所述,a≤-1或a>![]() 。
。
(2)![]() ,当a2-1=0时,若a=1,f(x)=lg(2x+1),符合题意,若a=-1,f(x)=0,不合题意。综上所述,1≤a≤
,当a2-1=0时,若a=1,f(x)=lg(2x+1),符合题意,若a=-1,f(x)=0,不合题意。综上所述,1≤a≤![]() 。
。
3.解:设![]() ,则f(x)=loga(at2-t),由对数函数定义,at2-t>0
,则f(x)=loga(at2-t),由对数函数定义,at2-t>0![]()
![]()
∵a>0,t>0,∴t>![]() ,又知
,又知![]() (
(![]() )是以t=
)是以t=![]() 为对称轴的抛物线,且
为对称轴的抛物线,且![]() ,因而g(t)在定义区间上是增函数,要使原函数在[2,4]上递增,应有
,因而g(t)在定义区间上是增函数,要使原函数在[2,4]上递增,应有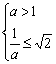 ,解之得:a>1,∴存在实数a,只须a>1,即满足条件。
,解之得:a>1,∴存在实数a,只须a>1,即满足条件。
4.解:∵![]() ∴1≤x≤3,又y=(log3x+2)2+log3x2+2=log32x+6log3x+2=(log3x+3)2-3,∵ 0≤log3x≤1,∴ ymax=13
∴1≤x≤3,又y=(log3x+2)2+log3x2+2=log32x+6log3x+2=(log3x+3)2-3,∵ 0≤log3x≤1,∴ ymax=13
5.解:①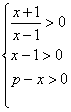
![]()
![]()
![]()
②![]()
![]()
![]() 当
当![]() ≤1时,即1
≤1时,即1![]() ≤3时,
≤3时, ![]() 无最大值和最小值。当1
无最大值和最小值。当1![]()
![]() p时,即
p时,即![]() 时,
时,![]()
![]() 取得最大值。
取得最大值。![]() ,但无最小值。
,但无最小值。
6.解:当![]() 时,
时,![]()
![]()
![]() 有最小值
有最小值![]() ,当
,当![]()
![]() 有最大值
有最大值![]()
②![]() 的对称轴为
的对称轴为![]() ,又
,又![]() 在
在![]() 上是单调函数,则
上是单调函数,则![]() ≤
≤![]() ,或
,或![]() ≥
≥![]() ,又
,又![]()
![]()
![]() ≤
≤![]() ≤
≤![]() 或
或![]() ≤
≤![]() ≤
≤![]() 故所求
故所求![]() 范围是
范围是![]()
7.![]()