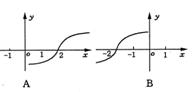怀仁中学2007届高三数学函数综合练习（2）
班级 姓名 学号
一、选择题：（每题5分，共60分）
1、设集合A={1，2，3}，集合B={a，b，c}，则从集合A到集合B的一一映射共有（ ）
A．3个 B．6个 C．9个 D．18个
2、设函数
的值是 （ ）
A．
B．
C．
D．2
3、给出两个命题：p：x=x的充要条件是x为正实数；q：存在反函数的函数一定是单调函
数，则下列哪个复合命题是真命题 （ ）
A．p且q B．p或q C．┐p且q D．┐p或q
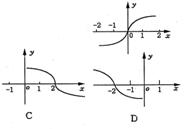
4、对函数
作代换x=g(t)，则总不改变f(x)值域的代换是 （ ）
A．
B．
C．g(t)=(t－1)2 D．g(t)=cost
5、函数
有且只有一个实根，那么实数a应满足（ ）
A．a<0 B．0<a<1 C．a=0 D．a>1
6、函数
的值域是 （
）
A．
B．
C．
D．
|
|
8、已知f(x)是定义在在R上的奇函数，且当x<0时，f(x)=2x,则f－1(－
)的值为（ ）
A．－
B． C．－2 D．2
9、设奇函数
上是增函数，且
若函数
对所有
的
都成立，当
时，则t的取值范围是 （ ）
A．
B．
C．
D．
10、设a>0为常数，若函数f(x)=x3－ax在区间
1，+∞
上是单调函数，则a的取值范围是（）A．（0，1
B．[1，+∞ C．（0，3 D．[3，+∞
11、关于函数
R且
），有下列三个结论： ①
的值域为R； ②是区间（0，+∞）上的增函数； ③对任意
R且
成立.
其中全部正确的结论是 （ ）
A．①②③ B．①③ C．①② D．②③
12、已知
是偶函数，当
恒成立，则
的最小值是 （ ）
A．
B．
C．1 D．
二、填空题（本大题共4个小题，每小题5分，共20分）
13. 当
且
时,指数函数
必过定点
.
14、函数
的图象与
轴的交点个数有
15、已知函数
在
上是增函数，则实数a的范围是 .
16．已知定义在R上的偶函数满足条件：
，且在[－1，0]上是增函数，给出下面关于的命题： ①是周期函数； ②的图象关于直线
对称；
③在[0，1]上是增函数
④在[1，2]上是减函数 ⑤
其中正确的命题序号是 .（注：把你认为正确的命题序号都填上）
三、 解答题：共70分，解答应写出文字说明、证明过程或演算步骤.
17. （本小题满分14分）设函数
,
(1)
求证:不论
为何实数总为增函数;（2）确定的值,使为奇函数;
（3）当为奇函数时,求的值域.
18、（本小题满分14分） 已知函数
.
（1）求的反函数；（2）设
，求函数
的最小值及相应的x的值.
19．（本小题满分12分）某厂家拟在2007年举行促销活动，经调查测算，该产品的年销售量（即该厂的年产量）x万件与年促销费用m万元（
）（k为常数），如果不搞促销活动，则该产品的年销售量只能是1万件。已知2004年生产该产品的固定投入为8万元，每生产1万件该产品需要再投入16万元，厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍（产品成本包括固定投入和再投入两部分资金）。
（1）将2007年该产品的利润y万元表示为年促销费用m万元的函数；
（2）该厂家2007年的促销费用投入多少万元时，厂家的利润最大？
20、（本小题满分14分）设函数在
上满足
，
，且在闭区间［0，7］上，只有
．
（Ⅰ）试判断函数
的奇偶性；
（Ⅱ）试求方程=0在闭区间［-2005，2005］上的根的个数，并证明你的结论．
21、（本小题16分）函数是偶函数，且是周期为2的周期函数，当x∈[2，3]时，
，在的图象上有两点A、B，它们的纵坐标相等，横坐标都在区间[1，3]上，定点C的坐标为（0,a）（其中a>2），求△ABC面积的最大值.
参考答案
一、BCDACD CDCCAC
二、13、
14、2 15、
16、①②⑤
三、17解析: 由
得
,而函数的定义域为
,
必有
或 },
当
时,
在上单调递减,
的值域是
解得
;
当
时, 在上单调递增,
的值域为
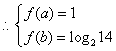解得
综上所述,知 或 
.
18、解：（1）由
得，
. 
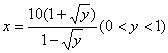（2）
等号成立的条件为
即
（舍去
）.
.
有最小值为
19．解：（1）由题意可知当
…2分
每件产品的销售价格为
……………………………………4分
∴2004年的利润
……………………6分
（2）
，………………………………9分
（万元）…11分
答：（略）……………………………………………………………………………12分
20、.解:由f(2-x)=f(2+x),f(7-x)=f(7+x)得函数的对称轴为
,
从而知函数不是奇函数,
由
,从而知函数的周期为
又
,故函数是非奇非偶函数;
(II)由
(II) 又
故f(x)在[0,10]和[-10,0]上均有有两个解,从而可知函数在[0,2005]上有402个解,在[-2005.0]上有400个解,所以函数在[-2005,2005]上有802个解.
21、 解：如图，∵f(x)是以2为周期的周期函数，
∴当
（平移），∵f(x)是偶函数，
∴当x∈[－1，0]时，
当x∈[1，2]时，f(x)=f(x－2)=－(x－2)+1=－x+3（平移）. 设A、B的纵坐标为t（1≤t≤2），并设A在B的左边，则A、B的横坐标分别为3－t，t+1，则AB=（t+1）－（3－t）=2t－2，△ABC的面积为
令
得
当
，即2＜a≤3时，S有最大值
当
，即a＞3时，
，函数单调增，S有最大值S（2）=a－2.
[这里可将S配方；S=
也可直接用二次函数理论得出].