怀仁中学 2007届高三数学函数综合练习(1)
班级 姓名 学号
一、选择题(每题5分,共60分)
1. 若函数ｙ＝ｆ（ｘ）存在反函数,则方程ｆ（ｘ）＝ｃ (c为常数) ( )
(A) 有且只有一个实根 (B)至少有一个实根 (C)至多有一个实根 (D)没有实根
2. 若ｆ（ｘ）＝（ｍ－１）ｘ２＋２ｍｘ＋３为偶函数,则ｆ（ｘ）在（－５，－２）
上的单调性是 ( )
（A）增函数 (B)减函数 (C)先增后减 (D)先减后增
3. 已知定义在R上的函数ｆ（ｘ）满足ｆ（ｘ＋ｙ）＝ｆ（ｘ）＋ｆ（ｙ）,且f (x)不恒为零,则ｆ（ｘ）是 ( )
(A) 奇函数 (B) 偶函数 (C) 既是奇函数又是偶函数 (D)非奇非偶函数
4. 下列函数在（０，１）上是减函数的是 ( )
(A)
(B)
(C)
(D)
5. 已知函数ｙ＝ｆ（ｘ）存在反函数ｙ＝ｇ（ｘ），若ｆ（３）＝－１，则函数ｙ＝ｇ（ｘ－１）的图象在下列各点中必经过 ( )
(A) （－２，３） (B) （０，３） (C) （２，－１） (D) （４，－１）
６．定义在R上的奇函数
为减函数，设
＋
＜0，则给出下列不等式（ ）
①
②
③
④
A．①② B．②④ C．①④ D．①③
7. 将函数f (x)=lg (1－x)的图象沿（ ）平移 1个单位所得的图象与函数y＝lgx的图象关于y轴对称．
(A) x轴向右 (B) x轴向左 (C)y轴向上 (D) y轴向下
8. 函数
在区间
上是减函数,则a的取值范围是
（ ）
(A) 
(B) 
(C)
(D)
９.某公司从2000年起，每人的年工资由三个项目组成并按下表规定实施
| 项目 | 计算办法 |
| 基础工资 | 2000年1万元，考虑物价因素，以后每年递增10% |
| 住房补贴 | 按工龄计算：400元×工龄(工龄计算方法，如某职工1998年进公司，到2001年按4年计算) |
| 医疗费 | 每年1600元，固定不变 |
该公司的一职工在2002年将得到的住房补贴和医疗费之和可超过基础工资的25%，这位职工的工龄至少是 ( )
(A)2年 (B)3年 (C)4年 (D)5年
10. 设ｆ（ｘ）＝3ax－2a＋1，若存在x0∈（－１，１），使ｆ（x0）＝０，则实数a的取值范围是 ( )
(A)
－1＜a＜
(B) a＜－1 (C)
a＜－1或a＞ (D) a＞
11.
设ｆ（ｘ）是定义在R上的偶函数，且对任意x都有ｆ（ｘ－１）＝ｆ（ｘ＋３），在［４，６］上
，那么在［－２，０］上ｆ（ｘ）的反函数可以表示 ( )
(A) ｙ＝log2（x－4） (B) ｙ＝4－log2（x－1）（C) ｙ＝4＋log2（x－1） (D)ｙ＝－log2（x－1）
12. 设ｘ≥０，ｙ≥０且,ｘ＋２ｙ＝
，则函数ｕ＝
的最大值为（ ）（A）
（B）０（C）１（D）
二、填充题(每题5分,共25分)
13.若函数ｆ（ｘ）的定义域是
，则F（ｘ）＝ｆ［log0.5（３－ｘ）］的定义域
是
14.若奇函数ｙ＝ｆ（ｘ）(x
0)在ｘ＞０时,ｆ（ｘ）＝ｘ－１,则使ｆ（ｘ－１）＜０的ｘ的取值范围是
15. 已知函数ｆ（ｘ）＝１０＋loga(x+
且ｆ（１）＝２则ｆ（－１）＝
16．某商场宣传在“五一黄金周”期间对顾客购物实行一定的优惠，商场规定：
①如一次性购物不超过200元，不予以折扣；
②如一次性购物超过200元但不超过500元的，按标价给予九折优惠；
③如一次性购物超过500元的，其中500元给予9折优惠，超过500元的部分给予八五折优惠．
某人两次去购物，分别付款176元和432元，如果他只去一次购买同样的商品，则应付款
17.定义在R上的偶函数ｆ（ｘ）满足ｆ（ｘ＋１）＝－ｆ（ｘ）,且在
［－１，０］上是增函数,则下列正确的是
①ｆ（ｘ）是周期函数 ； ②ｆ（ｘ）的图象关于直线ｘ＝１对称 ；
③ｆ（ｘ）在［０，１］上是增函数；④ｆ（ｘ）在［１，２］上是减函数；
⑤ｆ（２）＝ｆ（０）．
三、解答题（共65分）
18、（本小题共12分）
设f(x)是定义在R上的偶函数，在区间（－∞，0）上单调递增，且满足f(－a2+2a－5)<f(2a2+a+1),
求实数a的取值范围.
19. （本小题共12分）已知F（ｘ）＝ｆ（ｘ）－ｇ（ｘ）其中ｆ（ｘ）＝loga(ｘ－１),(ａ＞０，ａ
)，且当且仅当点(x0，y0)在ｆ（ｘ）的图象上时,点(2x0，2y0)在
ｙ＝ｇ（ｘ）的图象上.
（１）求ｙ＝ｇ（ｘ）的解析式
（２）当x在什么范围时,F（ｘ）≥０．
20. （本小题共12分） 函数ｆ（ｘ）＝ｘ２＋ａｘ＋３
（１）当x
R时,ｆ（ｘ）≥ａ恒成立,求a的取值范围
（２）当x［－２，２］时, ｆ（ｘ）≥ａ恒成立,求a的取值范围
21．（本小题满分14分）
已知函数
直线l : 
.
(1) 求证: 直线l与函数
的图像不相切;
(2) 若当
时, 函数的图像在直线l的下方, 求c的范围.
22． (本题满分15分)
对定义域分别是Df、Dg的函数y=f(x) 、y=g(x),
f(x)·g(x) 当x∈Df且x∈Dg
规定: 函数h(x)= f(x)
当x∈Df且x
Dg
g(x) 当xDf且x∈Dg
(1) 若函数f(x)=-2x+3 ,x≥1; g(x)=x-2,x∈R,写出函数h(x)的解析式;
(2) 求问题(1)中函数h(x)的最大值;
(3) 若g(x)=f(x+α), 其中α是常数,且α∈[0,π],请设计一个定义域为R的函数y=f(x),及一个α的值,使得h(x)=cos2x,并予以证明.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | A | A | D | B | C | B | B | C | C | B | B |
13 
14 
15 18
16 582.6元 17 ①②⑤
18．∵为R上的偶函数，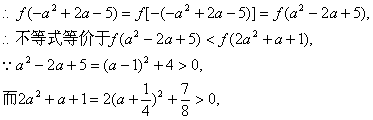 
∵在区间
上单调递增，而偶函数图象关于y轴对称， ∴在区间（0，+∞）上单调递减，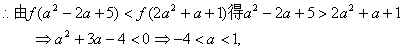
∴实数a的取值范围是（－4，1）.
19.解：（1）
（2）
，（其中
，即
） 
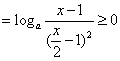
时， 
时， 
20.（1）
，
；
（2）①
，
，不可能；②
③
，
21．（本小题满分14分）
解: (1) 证明: 
……………2分
假设直线l : 与函数的图像相切, 则
有实数解, 即
有实数解. ……………5分
因为
时, 方程无实数解, 所以直线l与函数的图像不相切.……………7分
(2) 当
时, 函数的图像在直线l的下方,
即
对于一切都成立, ……………9分
即
对于一切都成立. ……………10分
令
因为
所以在
上单调递减, ……………12分
所以当时, 
……………13分
所以
, 所以c的范围是
……………14分
22. [解](1)h(x)= (-2x+3)(x-2) x∈[1,+∞)
x-2 x∈(-∞,1)
(2) 当x≥1时, h(x)= (-2x+3)(x-2)=-2x2+7x-6=-2(x-
)2+
∴h(x)≤; 当x<1时, h(x)<-1,
∴当x=时, h(x)取得最大值是
(3)令 f(x)=sinx+cosx,α=
则g(x)=f(x+α)= sin(x+)+cos(x+)=cosx-sinx,
于是h(x)= f(x)·f(x+α)= (sinx+cosx)( cosx-sinx)=cos2x.
另解令f(x)=1+
sinx, α=π,
g(x)=f(x+α)=
1+sin(x+π)=1-sinx,
于是h(x)= f(x)·f(x+α)= (1+sinx)( 1-sinx)=cos2x.