高三数学小题专项训练（1）
班级 学号 姓名 得分
1．sin600° = ( )
(A) –
(B)–
.
(C).
(D) .
2．设A = { x x ³ 2}, B = { x x – 1< 3}, 则A∩B= ( )
(A)[2，4] (B)（–∞，–2]
(C)[–2，4] (D)[–2，+∞）
3．若a=2sin150，b=4cos150，a与b的夹角为300，则a·b的值为 ( )
(A)
. (B)
. (C)
. (D)
.
4．△ABC中，角A、B、C所对的边分别为a、b、c，则acosC+ccosA的值为 ( )
(A)b. (B)
. (C)2cosB. (D)2sinB.
5．当x Î R时，令f (x )为sinx与cosx中的较大或相等者，设a £ f ( x ) £ b, 则a + b 等于 ( )
(A)0 (B) 1 + 
. (C)1–. (D)–1.
6、函数
在区间[0,1]上是（ ）
（A）单调递增的函数. （B）单调递减的函数.
（C）先减后增的函数 . （D）先增后减的函数.
7．对于x∈[0，1]的一切值，a +2b > 0是使ax + b > 0恒成立的（ ）
(A)充要条件 (B)充分不必要条件
(C)必要不充分条件 (D)既不充分也不必要条件
8．设{an}是等差数列，从{a1，a2，a3，··· ，a20}中任取3个不同的数，使这三个数仍成等差数列，则这样不同的等差数列最多有（ ）
(A)90个 . (B)120个. (C)180个. (D)200个.
9．已知函数y = f ( x )（x∈R）满足f (x +1) = f ( x – 1)，且x∈[–1，1]时，f (x) = x2，则y = f ( x ) 与y = log5x的图象的交点个数为 ( )
(A)1. (B)2 . (C)3 . (D)4.
10．给出下列命题：
(1) 若0< x <
, 则sinx < x < tanx . (2) 若– < x< 0, 则sin x < x < tanx.
(3) 设A，B，C是△ABC的三个内角，若A > B > C, 则sinA > sinB > sinC.
(4) 设A，B是钝角△ABC的两个锐角，若sinA > sinB > sinC 则A > B > C..
其中，正确命题的个数是（ ）
(A) 4. （B）3. （C）2. （D）1.
11. 某客运公司定客票的方法是：如果行程不超过100km，票价是0.5元/km， 如果超过100km， 超过100km部分按0.4元/km定价，则客运票价y元与行程公里数x km之间的函数关系式是 .
12. 设P是曲线y = x2 – 1上的动点，O为坐标原点，当
2取得最小值时，点P的坐标为 .
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
11、 . 12.
高三数学小题专项训练（2）
班级 学号 姓名 得分
1．函数
(x>1)的反函数是（ ）
（A）y=1+log2x (x>1) （B）y=1+log2x (x>0)
（C）y=－1+log2x (x>1) （D）y=log2(x－1) (x>1)
2．设集合A={(x, y) y=2sin2x}，集合B={(x, y) y=x}，则（ ）
（A）A∪B中有3个元素 （B）A∪B中有1个元素
（C）A∪B中有2个元素 （D）A∪B=R
3．焦点在直线3x－4y－12=0上的抛物线的标准方程为（ ）
（A）x2=－12y （B）y2=8x或x2=－6y
（C）y2=16x （D）x2=－12y或y2=16y
4．在△ABC中“A>B”是“cosA<cosB”的（ ）
（A）充分非必要条件 （B）必要非充分条件
（C）充要条件 （D）既不充分也不必要条件
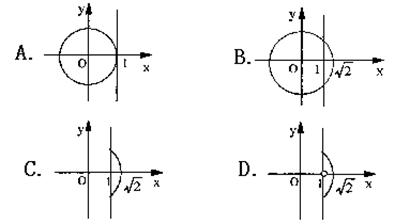
5．已知mn≠0，则方程mx2+ny2=1与mx+ny2=0在同一坐标系下的图象可能是（ ）
6．在数列{an}中，已知
(c∈R)，则对于任意正整数n有（ ）
（A）an<an+1 （B）an与an+1的大小关系和c有关
（C）an>an+1 （D）an与an+1的大小关系和n有关
二．填空题：
7．函数f(x)=
的定义域为
。
8．函数y=tanx－cotx的最小正周期为 。
9．已知向量
=(1, 0)，
=(2, 2)，则
=
。
10．已知点A(6, 0)，B为圆x2+y2=4上任意一点，则线段AB的中点M的轨迹方程为 。
11．设双曲线
(a>0, b>0)的焦距为2c，A、B分别为实轴与虚轴的一个端点，若坐标原点到直线AB的距离为
，则双曲线的离心率为
；渐近线方程为
。
12．设函数f(x)的定义域为R，若存在常数M>0，使f(x)≤Mx对于一切实数x均成立，则称f(x)为
函数，给出下列函数：① f(x)=0；② f(x)=x2；③ f(x)=
(sinx+cosx)；④ 
；⑤ f(x)是定义在R上的奇函数，且满足对于一切实数x1, x2，均有f(x1)－f(x2)≤2x1－x2，其中是函数的序号是
。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 答案 |
7、 . 8.
9、 . 10.
11、 . 12.
高三数学小题专项训练（3）
班级 学号 姓名 得分
1．设全集U={2，4，6，8，10}，集合A={2，4，6}，B={4，8}，则
=（ ）
（A）{4} （B）{4，6} （C）{6} （D）{2，6}
2．曲线
在点(1, －1)处的切线方程是（ ）
（A）y=3x－4 （B）y=－3x+2 （C）y=－4x+3 （D）y=4x－5
3．函数
(x≥1)的反函数是（ ）
（A）y=x2－2x+2 (x<1) （B）y=x2－2x+2 (x≥1)
（C）y=x2－2x (x<1) （D）y=x2－2x (x≥1)
4．若p是q的必要不充分条件，则
是
的（ ）
（A）充分不必要条件 （B）必要不充分条件
（C）充分且必要条件 （D）既不充分也不必要条件
5．某大楼共有20层，有19人在第一层上了电梯，他们分别要去第2层至第20层，每层1人，而电梯只允停1次，可只使1人满意，其余18人都要步行上楼或下楼，假设乘客每向下走1层的不满意度为1，每向上走一层的不满意度为2，所有人的不满意度之和为S，为使S最小，电梯应当停在第（ ）层。
A．12 B．13 C．14 D．15
6．函数
的定义域是（ ）
（A）
（B）(
, +∞) （C）[, 1] （D）
7．若
，则下列不等式① a+b<ab；② a>b；③ a<b；④ 
中，正确的不等式有（ ）
（A）1个 （B）2个 （C）3个 （D）4个
8．若函数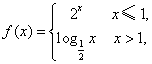
则y=f(1－x)的图象可以是（ ）
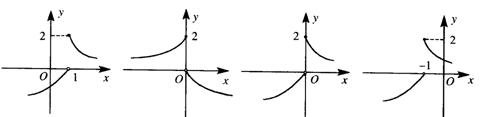
（A）
（B）
（C）
（D）
9．若等差数列{an}中，公差d=2，且a1+a2+a3+……+a100=200，则a5+a10+a15+……+a100的值是 .
10、f(x)在R上是奇函数，当x∈(0, +∞)时为增函数，且f(1)=0，则不等式f(x)<0的解集为 .
11、有两个命题：① 不等式
的解集是R；② 函数
是减函数，若这两个命题中有且只有一个真命题，则实数m的取值范围是
。
12、数
(x∈R)，若x1+x2=1，则f(x1)+f(x2)=
，又若n∈N*，则
=
.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 |
9 . 10
11、 . 12.
高三数学小题专项训练（4）
班级 学号 姓名 得分
1.如果向量 =(k，1)，与 = (4，k)共线且方向相反，则k =
A．±2 B．-2 C．2 D．0
2．函数f(x)=( )x(1<x≤2)的反函数f-1(x)等于
A.log x(1<x≤2)
B.
log x(2<x≤4)
C.-log2x(
≤x＜ ﹞
D. -log2x( ≤x＜1〕
3.已知P=｛x︱x≤0｝,Q=｛x︱x＜ ｝,则Q∩CRP等于
|
A.｛x︱x≤0｝ B.｛x︱0≤x＜ }
C. {x0<x< }
D. {xx>0}
4．已知α、β都是第二象限角，且cos >cosβ，则
A ． <β B．sin >sinβ C．tan >tanβ D．cot <cotβ
5．已知奇函数f(x)的定义域为：{x｜x+2-a｜＜a，a>0}，则a的值为
A．1 B．2 C．3 D．4
6．方程Ax+By+C=0表示倾斜角为锐角的直线，则必有：
A. A﹒B>0 B．A﹒B<0 C．A>0且B<0 D．A>0或B<0
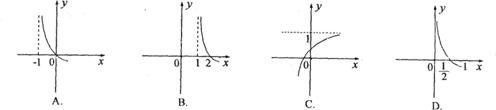
7．已知f(x)=ax(a>0且a≠1),f-1(2)<0，则f-1(x+1)的图象是
8．如果方程
表示双曲线，则下列椭圆中，与该双曲线共焦点的是
A. B.
C.
D.
9．把正整数按下图所示的规律排序，则从2003到2005的箭头方向依次为
10.已知函数f(x)=2sin(ωx+ )图象与直线y=1的交点中，距离最近两点间的距离为 ，
么此函数的周期是
A .
B．
C．2π
D．4π
11．点p到点A( ，0)，B(a，2)及到直线x=- 的距离都相等，如果这样的点恰好只有一个，那么a的值是
|  | | | | |
A. B. C. 或 D.- 或
 |
12.设 P(x,y)是曲线 上的点，F1(-4,0),F2(4,0),则
A.｜F1P︳+ ︱F2P︳<10 B．｜F1P｜+｜F2P｜>10
C.｜F1P︳+｜F2P︳≤10 D．｜F1P｜+｜F2P｜≥10
13．若函数 y=2x2+4x+3的图象按向量 平移后，得到函数y=2x2的图象，则： =
.
14．已知(x，y)在映射f下的象是(x+Y，-x)，则(1，2)在f下原象是 .
15．圆x2+y2+x-6y+3=0上两点P、Q关于直线kx-y+4=0对称，则k= .
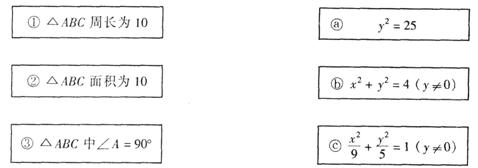
16.在△ABC中，B（-2，0），C（2，0），A（x,y）,给出△ABC满足的条件，就能得到动点A的轨迹方程，下面给出了一些条件及方程，请你用线把左边满足的条件及相应的右边A点的轨迹方程连起来：（错一条连线得0分）
高三数学小题专项训练（5）
班级 学号 姓名 得分
1．已知集合
Z），则集合
等于（ ）
A．{－1，1} B．{－1，0，1} C．{0，1} D．{－1，0}
2．函数
的最小正周期及最大值分别是 （ ）
A．
B．
C．
D．
3．下列函数中既是奇函数，又在区间
上单调递增的是 （ ）
A．
B．
C．
D．
4．直线
平行，则a等于 （ ）
A．
B．2 C．－1 D．2或－1
5．已知直线
平面
，直线
平面
，则下列命题正确的是（ ）
A．若
B．
C．
D．
6．设
（ ）
A．
B．
C．
D．
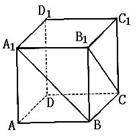
7．如右图，正方体ABCD—A1B1C1D1中，异面直线
A1B与B1C所成角的大小为
. 
8．已知
=2，
与 的夹角为45°，
则
=
.
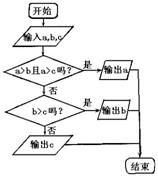
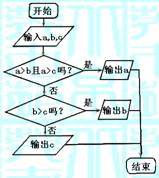
9．抛物线
，则p= ；点M到抛物线准线的距离为 . 10．如图所示的流程图是将一系列指令和问题用框图的形式排列而成，箭头将告诉你下一步到哪一个框图.阅读右边的流程图，并回答下面问题：
若
，则输出的数是 ； 若
则输出的
数是 .（用字母a，b，c填空）
|
11．已知向量
，则向量
的坐标是
，将向量按逆时针方向旋转90°得到向量
，则向量的坐标是
.
12．双曲线C：
的离心率为
，若直线
与双曲线C的交点在以原点为中心、边长为4且各边分别平行于两坐标轴的正方形内，则实数m的取值范围是
.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 答案 |
7 . 8
9 . 10
11、 . 12.
高三数学选择、填空专项训练（6）
班级 学号 姓名 得分
1．在下列各点中，不在不等式
表示的平面区域内的点为（ ）
A．（0，1） B．（1，0） C．（0，2） D．（2，0）
2．已知
，则
的值等于（ ）
A．
B．
C．
D．
3．若函数
是奇函数，则下列坐标表示的点一定在函数
图象上的是（ ）
A．
B．
C．
D．
4．与直线
平行的抛物线
的切线方程是（ ）
A．
B．
C．
D．
5．等比数列{an}中，a3＝4，a5＝16，则a9＝（ ）
A．256 B．－256 C．128 D．－128
6．在半径为10cm的球面上有A、B、C三点，如果
，∠ACB＝60°，则球心O到平面ABC的距离为（ ）
A．2cm B．4cm C．6cm D．8cm
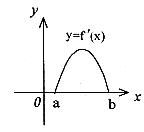7． f'（x）是f（x）的导函数，
的图象如图所示，则f(x)的图象只可能是（
）
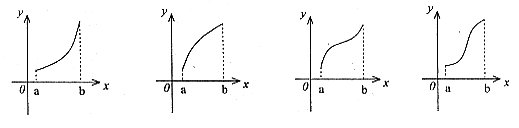A． B． C． D．
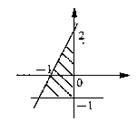
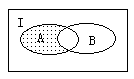8．图中阴影部分用集合符号表示为_____________。
9．函数
与函数的图象关于直线y＝x对称，则f(x)＝_____________；f(x)的定义域为_____________。
10．若直线l将圆
平分，且l不通过第四象限，则l斜率的取值范围为_________________________。
11．已知向量
的夹角为45°，且
，则
＝____________；
方向上的投影等于___________。
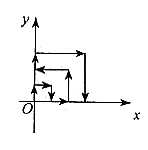
12．如图，一个粒子在第一象限运动，在第一秒内，它从原点运动到（0，1），接着它按如图所示的x轴、y轴的平行方向来回运动，（即（0，0）→（0，1）→（1，1）→（1，0）→（2，0）→…），且每秒移动一个单位，那么粒子运动到（3，0）点时经过了____________秒；2000秒时这个粒子所处的位置为____________。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 答案 |
8 9 .
10 11、 . 12.
高三数学选择、填空专项训练（7）
班级 学号 姓名 得分
1．设全集
，集合
CU M={5，7}，则a的值为（ ）
A．2 B．8 C．－2 D．－8
2．已知
是第二象限角，则
可化简为 （ ）
A．
B．－ C．
D．－
3．命题p：不等式
的解集为
命题q：“A=B”是“
”成立的必要非充分条件，则 （ ）
A．p真q假 B．“p且q”为真 C．“p或q”为假 D．p假q真
4．已知双曲线
的一条渐近线与直线
垂直，则该双曲线的准线方程是 （ ）
A．
B．
C．
D．
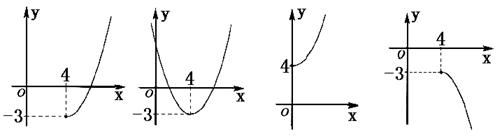
5．设函数
，则其反函数
的图象是（ ）
A
B
C
D
6．已知
，下列不等式正确的是 （ ）
A．
B．
C．
D．
7．在空间中，有如下命题：
①互相平行的两条直线在同一个平面内的射影必然是互相平行的两条直线；
②若平面//平面，则平面内任意一条直线m//平面；
③若平面与平面的交线为m，平面内的直线n⊥直线m，则直线n⊥平面；
④若点P到三角形三条边的距离相等，则点P在该三角形内部的射影是该三角形的内心.其中正确命题的个数为 （ ）
A．1个 B．2个 C．3个 D．4个
8．计算
=
.
9．函数
的图象F按向量
平移到F′，则F′的函数解析式为
.
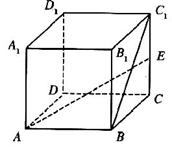10．如图，在正方体ABCD—A1B1C1D1中，CC1中点为E，
则AE与BC1所在的两条直线的位置关系是 ，
它们所成的角的大小为 .
11．已知数列
=
（用数字作答），设数列{
}的前n
项和为Sn，则S9= （用数字作答）.
12．已知函数
上是减函数，则a的取值范围是
.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 答案 |
8 9 .
10 11、 . 12.
高三数学选择、填空专项训练（8）
班级 学号 姓名 得分
1．若集合M={yy=－2－x}，P={yy=
},则M∩P= （ ）
A．{yy<0} B．{yy≥1} C．{yy≥0} D．
2．下列函数中，既是偶函数，又在（0，π）内单调递增的函数是 （ ）
A．y=tanx B．y=cos(－x) C．y=sin(x－
) D．y=cot
3．若实数a、b满足ab<0，则有 （ ）
A．a－b<a－b B．a－b<a+b
C．a+b>a－b D．a+b<a－b
4．图中阴影部分可用哪一组二元一次不等式表示 （ ）
|
B．
C．
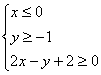D．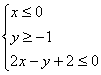
5．生物学指出：生态系统中，在输入一个营养级的能量中，大约10%的能量能够流到下一个营养级.在H1→H2→H3这个生物链中，若能使H3获得10kj的能量，则需H1提供的能
量为 （ ）
A．105kj B．104kj C．103kj D．102kj
6．给定两个向量
，则x的等于（ ）
A．－3 B． C．3 D．－
7．若某等差数列{an}中，a2+a6+a16为一个确定的常数，则其前n项和Sn中也为确定的常数的是 （ ）
A．S17 B．S15 C．S8 D．S7
8． 将一张画了直角坐标系且两轴的长度单位相同的纸折叠一次，使点（2，0）与点
（－2， 4）重合，若点（7，3）与点（m ,n）重合，则m+n的值为
A．4 B．－4 C．10 D．－10
9．方程
所表示的曲线图形是 （ ）
|
10．已知
.
11．在一个水平放置的底面半径为的圆柱形量杯中装有适量的水，现放入下个半径为R的实心铁球，球完全浸没于水中且无水溢出，若水面高度恰好上升R，则R=
.
12．设函数
，则方程
的解为
.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 答案 |
10、 . 11、 . 12.
高三数学选择、填空专项训练（9）
班级 学号 姓名 得分
1．设
，则
的值为 （ ）
A．
B．－ C．
D．－
2．设条件A：几何体的各个面都是三角形，条件B：几何体是三棱锥，则条件A是条件B的 （ ）
A．充分而不必要条件 B．必要而不充分条件
C．充要条件 D．既不充分也不必要条件
|
|
，则函数的图象为 （ ）
4．设集合M={a，b，c}，N={0，1}，映射f：M→N满足
，则映射f：M→N的个数为 （ ）
A．1 B．2 C．3 D．4
5．圆心在抛物线
上，并且与抛物线的准线及y轴都相切的圆的方程为
（ ）
A．
B．
C．
D．
6．过△ABC的重心任作一直线分别交AB、AC于点D、E.若
则
的值为 （ ）
A．4 B．3 C．2 D．1
7．给出下列命题：
①
②把正方形ABCD平移向量
到A′B′C′D′的轨迹形成的几何体叫做正方体；
③
=“从济南往正比平移3km”，
=“从济南向正北平移6km”，则=2.
其中正确的命题是 （ ）
A．①② B．②③ C．①②③ D．①③
8．设三棱锥的三个侧面两两互相垂直，且侧棱长均为，则其外接球的表面积为（ ）
A．48
B．36 C．32 D．12
9．设
是函数F(x)的单调递增区间，将F(x)的图象按a
平移得到一个新的函数G(x)的图象，则G(x)的单调递减区间必定是（ ）
A．
B．
C．
D．
10．若双曲线
过点
，则该双曲线的焦距为 .
11．某地区预计2004年的前x个月内对某种商品的需求总量
（万件）与月份
的近似关系式是
，则2004年的第x月的需求量g(x)（万件）与月份x的函数关系式是
.
12．若直线y=x是曲线
的切线，则a=
.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 答案 |
10、 . 11、 . 12.
高三数学选择、填空专项训练（10）
班级 学号 姓名 得分
1．下列各组中，M是N的充要条件的是 （ ）
A．M：x+y≤1，N：x2+y2≤1, B．M：实数a、b，a+b>2，且ab>1,N：a>1且b>1
C．M：集合E、F和P，P
E且PF，N：PE∩F
D．M：－3≤t≤3，N：曲线y=
（y≠0）与直线y=x+t有公共点
2．设3a=4,3b=12,3c=36，那么数列a，b，c
Ａ．是等差数列但不是等比数列 B．是等比数列但不是等差数列
Ｃ．既是等差数列也是等比数列 Ｄ．既不是等差数列也不是等比数列
3．函数f(x)=sin(2x+φ)+cos(2x+φ)的图像关于原点对称的充要条件是
A．φ=2kπ－，k∈Z B．φ=kπ－，k∈Z
C．φ=2kπ－，k∈Z D．φ=kπ－，k∈Z
4．将棱长为3的正四面体的各棱长三等份，经过分点将原正四面体各顶点附近均截去一个棱长为1的小正四面体，则剩下的多面体的棱数E为
A．16 B．17 C．18 D．19
5．设ｆ(x)= x2+ax+b，且1≤f(－1)≤2，2≤f(1)≤4，则点(a，b)在aOb平面上的区域的面
积是
A．
B．1
C．2
D．
6．已知向量
=(2,1)，
=(1,7)，
=(5,1)，设X是直线OP上的一点(O为坐标原点)，那么
的最小值是
A．－16 B．－8 C．0 D．4
7．直线 + =1与椭圆 + =1相交于A、B两点，椭圆上的点P使△PAB的面积等于12．这样的点P共有
A．1个 B．2个 C 3个 D．4个
8．
函数y=f(x)与y=g(x)有相同的定义域，且都不是常数函数，对定义域中任何x，有f(x)+f(－x)=0，g(x)·g(－x)=1，且当x≠0时，g(x) ≠1，则
＝＋
A．是奇函数但不是偶函数 B．是偶函数但不是奇函数
C．既是奇函数又是偶函数 D．既不是奇函数也不是偶函数
9．当x∈［0,2］时，函数f(x)=ax2+4(a－1)x－3在x=2时取得最大值，则a的取值范围是
A．[－
,+∞)
B．[0，+∞）
C．[1, +∞)
D．[
,+∞)
10．已知直线ax+by+1=0中的a，b是取自集合{－3，－2，－1，0，1，2}中的2个不同的元素，并且直线的倾斜角大于60°，那么符合这些条件的直线的共有
A．8条 B．11条 C．13条 D．16条
11．不等式(x－2)≥0的解集是 ．
12．给出下列四个命题：
①过平面外一点，作与该平面成θ角的直线一定有无穷多条；
②一条直线与两个相交平面都平行，则它必与这两个平面的交线平行；
③对确定的两条异面直线，过空间任意一点有且只有唯一的一个平面与这两条异面直线都平行；
④对两条异面的直线，都存在无穷多个平面与这两条直线所成的角相等；
其中正确的命题序号为 （请把所有正确命题的序号都填上）．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
11、 . 12.