高三数学一轮复习
三角函数测试卷
一、选择题：本大题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的．
1．集合A={
，B={
，
则A、B之间关系为 （ ）
A．
B．
C．B
A D．AB
2．函数
的单调减区间为 （ ）
A．
B．
C．
D．
3．设角
则
的值等于 （ ）
A．
B．－ C．
D．－
4．已知锐角
终边上一点的坐标为（
则= （ ）
A．
B．3 C．3－
D．－3
5．函数
的大致图象是 （ ）
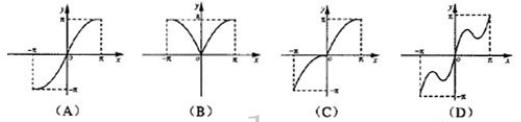
6．下列函数中同时具有①最小正周期是π；②图象关于点（
,0）对称这两个性质的是（ ）
A.
y＝cos（2x＋） B．y＝sin（2x＋） Ｃ．y＝sin（
＋）Ｄ．y＝tan（x＋）
7．已知
的图象和直线y=1围成一个封闭的平面图形，该图形的面积
是 （ ）
A．4π B．2π C．8 D．4
8．与正弦曲线
关于直线
对称的曲线是（ ）
A． B．
C．
D．
9. 若方程
恰有两个解，则实数
的取值集合为
（ ）
A. 
B. 
C. 
D. 
10．已知函数
在同一周期内，
时取得最大值
，
时取得最
小值－，则该函数解析式为 （
）
A．
B．
C
D．
11．.函数
的图象的相邻两支截直线
所得线段长为
，则
的值是
（ ）
A．0 B．1 C．-1 D．
12．函数
上为减函数，则函数
上
（ A ）
A．可以取得最大值M B．是减函数 C．是增函数 D．可以取得最小值－M
二、填空题：本大题共4小题，把答案填在题中横线上．
13．已知
,这
的值为
14．在区间
上满足
的
的值有 个
15．设
，其中m、n、
、
都是非零实数，若 
则
.
16．设函数
，给出以下四个论断：
①它的图象关于直线
对称； ②它的图象关于点
对称；
③它的周期是
；
④在区间
上是增函数。
以其中两个论断作为条件，余下论断作为结论，写出你认为正确的两个命题：
（1）_________________ ； （2）__________________.（用序号表示）
三、解答题：本大题共6小题，解答应写出文字说明、证明过程或演算步骤．
17．若
, 求角的取值范围.
18．说明函数
的图像可以由函数
的图像经过怎样的变换得到。
19．已知
，求
的值。
20．设
满足
,
（１）求的表达式； （２）求的最大值．
21．已知
,求
的最值。
22．已知函数
是R上的偶函数，其图象关于点
对称，且在区间
上是单调函数.求
的值.
参考答案
1.C 2. B 3.C 4.C 5.C 6. A 7.B 8 D 9.D 10.B 11.A 12.A
13. 
14. 5 15.－1 16.(1) ①③
②④ (2) ②③①④
17．左
=右，
18．可先把的图像上所有点向右平移
个单位，得到
的图像，再把图像上的所有点的横坐标伸长到原来的2倍（纵坐标不变），从而得到的图像。
19．
=
=
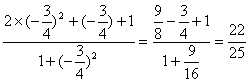
20．
①
得
②
由３
①－②，得8
， 故
．
（２）对
，将函数的解析式变形，得
＝
，当
时，
21．
代入
中，得
又
22．解：由f(x)是偶函数，得f(－x)= f(－x).
即： 
所以－
对任意x都成立，且
所以得
=0.依题设0
，所以解得
，
由f(x)的图象关于点M对称，得
.取x=0,得
=－，所以=0.
