应用题
1．某集团公司为了获得更大的收益，每年要投入一定的资金用于广告促销。经调查,每投入广告费
(百万元)，可增加销售额约为
（百万元）（0≤≤5）。
(1)若该公司将当年的广告控制在3百万元之内，则应投入多少广告费，才能使该公司由此获得的收益最大？
(2)该公司准备共投入3百万元，分别用于广告促销和技术改造。经预测，每投入技术改造费
（百万元），可增加的销售额约为
）。请设计一个资金分配方案，使该公司由此获得的收益更大？（
）
2．甲方是一农场，乙方是一工厂. 由于乙方生产须占用甲方的资源，因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入，在乙方不赔付甲方的情况下，乙方的年利润x（元）与年产量t（吨）满足函数关系
.
若乙方每生产一吨产品必须赔付甲方s元（以下称s为赔付价格），
（1）将乙方的年利润w（元）表示为年产量t（吨）的函数，并求出乙方获得最大利润的年产量；
（2）甲方每年受乙方生产影响的经济损失金额
（元），在乙方按照获得最大利润的产量进行生产的前提下，甲方要在索赔中获得最大净收入，应向乙方要求的赔付价格s是多少？
3.已知某商品的价格上涨
%，销售的数量就减少
%，其中
为正的常数.
（1）当
时，该商品的价格上涨多少，就能使销售的总金额最大？
（2）如果适当地涨价，能使销售总金额增加，求的取值范围.
4．某农产品去年各季度的市场价格如下表：
| 季 度 | 第一季度 | 第二季度 | 第三季度 | 第四季度 |
| 每担售价（单位：元） | 195.5 | 200.5 | 204.5 | 199.5 |
今年某公司计划按去年各季度市场价的“最佳近似值m”（m是与上表中各售价差的平方和取最小值的值）收购该种农产品，并按每100元纳税10元（又称征税率为10个百分点，计划可收购a万担，政府为了鼓励收购公司多收购这种农产品，决定将税率降低x个百分点，预测收购量可增加2x个百分点.
（1）根据题中条件填空，m= （元/担）；
（2）写出税收y（万元）与x的函数关系式；
（3）若要使此项税收在税率调节后不少于原计划税收的83.2%，试确定x的取值范围.
5．某厂家拟在2003年国庆节期间举行促销活动，经调查测算，该产品的年销量（即该厂的年产量）x万件与年促销费用m万元（
）满足
（k为常数），如果不搞促销活动，该产品的年销售量只能是1万件，已知2003年生产该产品的固定投入为8万元，每生产1万件产品需要投入16万元，厂家将每件产品的销售价格定为年平均每件产品成本的1.5倍（产品成本包括固定投入和再投入两部分资金）
（1）将2003年该产品的利润y万元表示为年促销费用m万元的函数；
（2）该厂家2003年的促销费用投入多少万元时，厂家的年利润最大？
6．某公司取消福利分房和公费医疗，实行年薪制工资结构改革，该公司从2000年起每人的工资由三个项目并按下表规定实施
| 项目 | 金额（元/人·年） | 性质与计算方法 |
| 基础工资 | 一万元 | 考虑物价因素，从2000年起每年递增10%（与工龄无关） |
| 房屋补贴 | 400元 | 按照职工到公司的年限计算，每年递增400元 |
| 医疗费 | 1600元 | 固定不变 |
如果公司现有5名职工，计划从明年起每年新招5名职工
（Ⅰ）若今年（2000年）算第一年，试把第n年该公司付给职工工资总额y(万元)表示成年限n的函数；
（Ⅱ）试判断公司每年发给职工工资总额中，房屋补贴和医疗费的总和能否超过基础工资总额的20%？
7．某集团准备兴办一所中学，投资1200万用于硬件建设.为了考虑社会效益和经济利益，对该地区教育市场进行调查，得出一组数据列表（以班为单位）如下：
| 班级学生数 | 配备教师数 | 硬件建设（万元） | 教师年薪（万元/人） | |
| 初中 | 60 | 2.0 | 28 | 1.2 |
| 高中 | 40 | 2.5 | 58 | 1.6 |
根据有关规定，除书本费、办公费外，初中生每年可收取学费600元，高中生每年可收取学费1500元.因生源和环境等条件限制，办学规模以20至30个班为宜.根据以上情况，请你合理规划办学规模使年利润最大，最大利润多少万元？
（利润=学费收入－年薪支出）
8． 某县一中计划把一块边长为20米的等边三角形ABC的边角地辟为植物新品种实验基地，图中DE需把基地分成面积相等的两部分，D在AB上，E在AC上。
（1） 设AD=x(x≥10)，ED=y，试用x表示y的函数关系式；
（2） 如果DE是灌溉输水管道的位置，为了节约，则希望它最短，DE的位置应该在哪里？如果DE是参观线路，则希望它最长，DE的位置又应该在哪里？说明现由。
 |
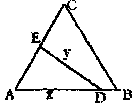9．A村在B地正北
km处，C村在B地正东4km处，已知弧形公路PQ上任一点到
B、C距离之和为8km,现在要在公路旁建造一个变电房M分别向A村、C村送电，但C村有一村办工厂用电需用专用线路，不得与民用混线用电，因此在C村要架两条线路分别给村民和工厂送电，要使得所用电线长最短，变电房M应建在A村的什么方位，并求出M到A村的距离。
1解：(1)设投入t（百万元）的广告费后增加的收益为f(t)(百万元)，则有
当t=2百万元时，f(t)取得最大值4百万元。即投入2百万元广告费时，该公司由此获得的收益最大。
(2) 设用于技术改造的资金为x（百万元），则用于广告促销的资金为（
）（百万元）（0≤x≤3），又设由此获得的收益是
，则有
，解得
.
.
即将2百万元用于技术改造，1百万元用于广告促销时，该公司由此获得的收益最大.
2．解：因为赔付价格为s元/吨,所以乙方的实际年利润为：
.（2分）
由
，令
得
.
（5分）
当
时，
；当
时
，所以
时， 
取得最大值.（可略）
因此乙方取得最大年利润的年产量
（吨）.
（6分）
（2）设甲方净收入为
元，则
.
（8分）
将
代入上式，得到甲方净收入与赔付价格
之间的函数关系式
.
又
，令
，得
.（11分）
当
时，
；当
时，
，所以时，取得最大值.
因此甲方向乙方要求赔付价格
（元/吨）时，获最大净收入。
3解：（1）设商品现在定价
元，卖出的数量为
个。
由题设：当价格上涨x%时，销售总额为
，
即 
，（
），
取得：
，当
时，
，
即：该商品的价格上涨50%时，销售总金额最大。
（2）二次函数，
在 
上递增，在
上递减，
适当地涨价能使销售总金额增加，即 在
内存在一个区间，使函数
在此区间上是增函数，所以 
，
解得
，即所求
的取值范围是 
4．（1）200；
（2）降低税率后的税率为（10－x）%，农产品的收购量为
万担，收购总金
额为
. 依题意，
（3）原计划税收为
（万元），依题意，
得
，
即
答：的取值范围是
.5 解：（1）设2003年生产产品x万件
时，
代入
则年成本：
年利润：
（2）
当且仅当
，即
时取等号
时，
万元
6.解：（Ⅰ）第n年共有5n个职工，那么基础工资总额为5n(1+
)n（万元）
医疗费总额为5n×0.16万元，房屋补贴为
5×0.04+5×0.04×2+5×0.04×3+…+5×0.04×n=0.1×n(n+1)（万元）
∴y=5n(1+)n+0.1×n(n+1)+0.8n
=n［5(1+)n+0.1(n+1)+0.8］（万元）
（Ⅱ）5(1+)n×20%-［0.1(n+1)+0.8］
=(1+)n-(n+9)
=［10(1+)n-(n+9)］
∵10(1+)n=10(1+Cn1Cn1+Cn2
+…)
＞10(1+
)＞10+n＞n+9
故房屋补贴和医疗费总和不会超过基础工资总额的20%
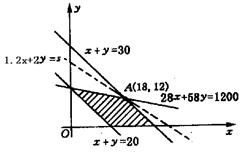
7解：设初中x个班，高中y 个班，则
……………（4分）
设年利润为s，则
……（6分）
作出（1）、（2）表示的平面区域，如图，易知当直线1.2x+2y=s过点A时，s有最大值.
|
解得A（18，12）.……（10分）
（万元）.
即学校可规划初中18个班，高中12个班，
可获最大年利润为45.6万元.……（12分）