高三数学月考试卷 2006 .9.26
一、 选择题:(每题5分,共50分;)
1.集合![]() =(
)
=(
)
A.![]() B.{1} C.{0,1,2} D. {-1,0,1,2}
B.{1} C.{0,1,2} D. {-1,0,1,2}
2.下列函数中,与y=x表示同一函数的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3.函数![]() 的单调增区间是( )
的单调增区间是( )
A、(-∞,1) B、(2,+∞) C、(-∞,![]() ) D、(
) D、(![]() ,+∞)
,+∞)
4.已知等差数列![]() 满足
满足![]() 则有 ( )
则有 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知![]() 则
则![]() 等于(
)
等于(
)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6.在一次数学实验中, 运用图形计算器采集到如下一组数据: B
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
则![]() 的函数关系与下列哪类函数最接近?(其中
的函数关系与下列哪类函数最接近?(其中![]() 为待定系数)
为待定系数)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知集合![]() ,集合B={xx>a},若A∩B=
,集合B={xx>a},若A∩B=![]() ,则a的取值范围是:(
)
,则a的取值范围是:(
)
A.![]() B.a≥1
C.a<1 D.
B.a≥1
C.a<1 D. ![]()
8.若函数![]() 在
在![]() 上存在x0,使f (x0)=0,则实数m的取值范围( )
上存在x0,使f (x0)=0,则实数m的取值范围( )
A、[![]() ,4] B、
,4] B、![]() C、[-1,2] D、[-2,1]
C、[-1,2] D、[-2,1]
9.函数y=x(1-x)在区间A上是增函数,则A区间是( )
A ![]()
![]() B
B ![]() C
C ![]() D(
D(![]()
10.函数![]() 的图像是:( )
的图像是:( )
 A
B
C
D
A
B
C
D
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二、填空题:本大题共6小题,每小题5分,共30分.)
11.函数![]()
![]()
![]() 的定义域为______________
的定义域为______________
12.计算:![]()
![]()
![]() _____________
_____________![]()
13.函数![]() ,
,![]() ___________(要求写出
___________(要求写出![]() 的定义域)
的定义域)
14.若函数![]() ,则xf(x)+x
,则xf(x)+x![]() 的解集是___________________
的解集是___________________
15已知![]() 且
且![]() 则
则![]() .
.
16.若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为![]() ,值域为{1,4}的“同族函数”共有_________________
,值域为{1,4}的“同族函数”共有_________________
三、 解答题:本大题共5小题,共70分。
17.(本题满分12分)
设集合M={(x,y) y=x2+ax+2},集合N={(x,y) y=x+1},若M![]() N中有两个元素,求实数a的取值范围.
N中有两个元素,求实数a的取值范围.
18.(本小题满分14分)设{an}为等差数列,Sn为数列{an}的前n项和,已知S7=7,S15=75,Tn为数列{![]() }的前n项和,求Tn
}的前n项和,求Tn
19. (本小题满分14分)f(x)=![]() ,x∈R
,x∈R
(1)证明:对任意实数a,f(x)在(-∞,+∞)上是增函数;
(2)当f(x)为奇函数时,求a;
(3)当f(x)为奇函数时,对于给定的正实数k,解不等式![]() 。
。
20. (本小题满分14分)已知g(x)=-x2-3,f(x)是二次函数,当x∈[-1,2]时,f(x) 的最小值是1,且f(x)+g(x)为奇函数,求f(x)解析式。
![]()
21. (本小题满分16分)已知集合![]() 是满足下列性质的函数
是满足下列性质的函数![]() 的全体:在定义域内存在
的全体:在定义域内存在![]() ,使得
,使得![]() 成立.
成立.
(1)函数![]() 是否属于集合
是否属于集合![]() ?说明理由;
?说明理由;
(2)设函数![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)判断方程![]() 的实根个数并证明:函数
的实根个数并证明:函数![]() .
.
CCACA BABDA
11.![]() 12.
12.![]()
![]() 13.
13.![]() 14.
14. ![]() 15.0 16.9
15.0 16.9
17.解:要使M![]() N中有两个元素,即曲线y=x2+ax+2与y=x+1有两个不同的交点,………2′
N中有两个元素,即曲线y=x2+ax+2与y=x+1有两个不同的交点,………2′
联立方程组得![]() (*)………5′
(*)………5′
∴方程(*)有两个不同的解,………………………………………………………………7′
∴△=(a-1)2-4>0;………………………………………………………………………9′
所以:a>3 或a<-1;
所以M![]() N中有两个元素时,实数a的取值范围是{ a a>3 或a<-1}.……………12′
N中有两个元素时,实数a的取值范围是{ a a>3 或a<-1}.……………12′
18.设等差数列{an}公差为d,则Sn=na1+![]() n(n-1)d
n(n-1)d
∵S7=7,S15=75,∴![]()
![]()
![]()
∴a1=-2,d=1,∴![]() =a1+
=a1+![]() (n-1)d=-2+
(n-1)d=-2+![]() (n-1)
(n-1)
∵![]() -
-![]() =
=![]()
∴{![]() }为等差数列,其首项为-2,公差为
}为等差数列,其首项为-2,公差为![]() ,
,
∴Tn=![]() n2-
n2-![]() n.
n.
19.(Ⅰ):![]() f(x) 是R上的奇函数,
f(x) 是R上的奇函数,![]() f(0)=0 得a=1………………………4分
f(0)=0 得a=1………………………4分
(Ⅱ) ∵y=![]() ∴y+y·2x=2x-1
∴y+y·2x=2x-1 ![]() 2x(y-1)=-1-y,2x=
2x(y-1)=-1-y,2x=![]() 即:f-1(x)=log2
即:f-1(x)=log2![]() (-1<x<1)……………………………8分
(-1<x<1)……………………………8分
(Ⅲ)log2![]() >log2
>log2![]() 等价于
等价于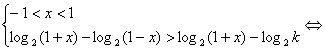
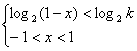
![]()
![]() …………………12分
…………………12分
(i)-1<1-k<1,即0<k<2时,{![]() }………………13分
}………………13分
(ii)1-k![]() -1,即k
-1,即k![]() 2时,{
2时,{![]() }…………………14分
}…………………14分
20.用待定系数法求f(x)解析式
设f(x)=ax2+bx+c(a≠0)
则f(x)+g(x)=(a-1)x2+bx+c-3
由已知f(x)+g(x)为奇函数![]()
∴ ![]()
∴ f(x)=x2+bx+3
下面通过确定f(x)在[-1,2]上何时取最小值来确定b,分类讨论。
![]() ,对称轴
,对称轴![]()
(1)当![]() ≥2,b≤-4时,f(x)在[-1,2]上为减函数
≥2,b≤-4时,f(x)在[-1,2]上为减函数
∴ ![]()
∴ 2b+7=1
∴ b=3(舍)
(2)当![]() (-1,2),-4<b<2时
(-1,2),-4<b<2时
![]()
∴ ![]()
∴ ![]() (舍负)
(舍负)
(3)当![]() ≤-1,b≥2时,f(x)在[-1,2]上为增函数
≤-1,b≥2时,f(x)在[-1,2]上为增函数
∴ (f(x)min=f(1)=4-b
∴ 4-b=1
∴ b=3
∴ ![]() ,或
,或![]()
21.解:(1)若![]()
![]() ,则在定义域内存在
,则在定义域内存在![]() ,使得
,使得![]() ,
,
∵方程![]() 无解,∴
无解,∴![]()
![]() .……(4分)
.……(4分)
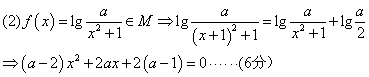 ,
,
当![]() 时,
时,![]() , ……(7分);当
, ……(7分);当![]() 时,由
时,由![]() ,
,
得![]() . ∴
. ∴![]() . …(9分)
. …(9分)
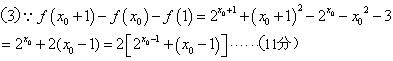 ,
,
又∵函数![]() 图象与函数
图象与函数![]() 的图象有交点,设交点的横坐标为
的图象有交点,设交点的横坐标为![]() ,
,
则![]() ,其中
,其中![]() ,……(14分)
,……(14分)
∴![]() ,即
,即![]() .……(15分)
.……(15分)