第一讲 集合与函数
陕西特级教师 安振平
l 高考风向标
本讲的主要内容是:集合的有关概念和运算,含有绝对值的不等式及一元二次不等式的解法,逻辑关联词,四种命题,充要条件.映射的概念,函数的概念,函数的单调性,反函数的概念,分数指数幂的概念和性质,指数函数的图象和性质,对数的定义和运算性质,对数函数的图象与性质,函数的一些应用.
l 典型题选讲
例1 在![]() 中,“
中,“![]() ”是“
”是“![]() ”的什么条件?
”的什么条件?
讲解 在![]() 中,角A、B的对边分别是
中,角A、B的对边分别是![]()
![]() 是
是![]() 的外接圆的半径.
的外接圆的半径.
一方面,因为 A<B,所以a<b ,
即![]() ,亦即
,亦即 ![]() ,从而
,从而![]() 中
中
A<B![]()
![]() 。
。
另一方面,因为![]() ,
,
所以![]() ,即
,即 ![]() ,得A<B,
,得A<B,
从而![]() 中,
中,![]()
![]() A<B。
A<B。
故![]() 中,“
中,“![]() ”是“
”是“![]() ” 的充要条件.
” 的充要条件.
点评 试问:在![]() 中,“
中,“![]() ”是“
”是“![]() ”的什么条件?
”的什么条件?
例2 试构造一个函数![]() ,使得对一切
,使得对一切![]() 有
有![]() 恒成立,但是
恒成立,但是![]() 既不是奇函数又不是偶函数,则
既不是奇函数又不是偶函数,则![]() 可以是
.
可以是
.
讲解 ![]() 的图像部分关于原点对称,部分关于
的图像部分关于原点对称,部分关于![]() 轴对称,如
轴对称,如
 .
.
点评 本题是一道开放题,你能给出其它的答案吗?请不妨一试.
 例3 某种细胞分裂时,由1个分裂成2个,2个分裂成4个,…,一直分裂下去.
例3 某种细胞分裂时,由1个分裂成2个,2个分裂成4个,…,一直分裂下去.
(1) 用列表表示,1个细胞分裂1、2、3、4、5、6、7、8次后,得到的细胞个数;
(2)用图像表示1个细胞分裂的次数n(nÎN+)与得到的细胞个数y之间的关系;
(3)写出得到的细胞个数y与分裂次数n之间的关系式,试用计算器算算细胞分裂15次、20次得到的细胞个数.
讲解 (1) 利用正整指数幂的运算法则,可以算出1个细胞分裂1、2、3、4、5、6、7、8次后,得到的细胞个数,列表如下
| 分裂次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 细胞个数 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 |
(2)细胞个数y与分裂次数n之间的关系式是
y=2n,nÎN+.
利用计算器可以算得
215=32768,220=.
故细胞分裂15次、20次得到的细胞个数分别是32768个和个.
点评 细胞分裂是一种很有趣的数学问题,我们也可以思考下面的类似的问题:
一种专门占据内存的计算机病毒,开机时占据内存![]() KB,然后每
KB,然后每![]() 分钟自身复制一次,复制后所占内存是原来的
分钟自身复制一次,复制后所占内存是原来的![]() 倍,那么开机后经过 ______ 分钟,该病毒占据
倍,那么开机后经过 ______ 分钟,该病毒占据![]() MB内存(
MB内存(![]() MB=
MB=![]() KB).
KB).
例4 已知函数![]() 的反函数
的反函数![]() ,
,![]()
(1)若![]() ,求
,求![]() 的取值范围
的取值范围![]() ;
;
(2)设函数![]() ,当
,当![]() 时,求
时,求![]() 的值域.
的值域.
讲解 ∵ ![]() ,
,
∴ ![]() .
.
(1)∵![]() 即
即![]() .
.
∴![]() ,
,
∴
解之得 ![]() ,
,
∴![]() .
.
(2) ∵ ![]()
![]()
![]()
![]() .
. ![]()
令![]() ,显然在[0,1]递增,
,显然在[0,1]递增,
则有 ![]() .
.
∴![]() ,即
,即![]() 的值域为
的值域为![]() .
.
例5 某厂生产一种仪器,由于受生产能力和技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率![]() 与日产量
与日产量![]() (件)之间大体满足关系:
(件)之间大体满足关系:
 (其中c为小于96的正常数)
(其中c为小于96的正常数)
注:次品率![]() ,如
,如![]() 表示每生产10件产品,约有1件为次品.其余为合格品.
表示每生产10件产品,约有1件为次品.其余为合格品.
已知每生产一件合格的仪器可以盈利A元,但每生产一件次品将亏损![]() 元,故厂方希望定出合适的日产量.
元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器每天的盈利额![]() (元)表示为日产量
(元)表示为日产量![]() (件)的函数;
(件)的函数;
(2)当日产量为多少时,可获得最大利润?
讲解 (1)当![]() 时,
时,![]() ,所以,每天的盈利额
,所以,每天的盈利额![]() ;
;
当![]() 时,
时,![]() ,所以,每日生产的合格仪器约有
,所以,每日生产的合格仪器约有![]() 件,次品约有
件,次品约有![]() 件.故,每天的盈利额
件.故,每天的盈利额
 .
.
综上,日盈利额![]() (元)与日产量
(元)与日产量![]() (件)的函数关系为:
(件)的函数关系为:

(2)由(1)知,当![]() 时,每天的盈利额为0.
时,每天的盈利额为0.
当![]() 时,
时,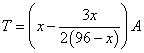 .
.
令![]() ,则
,则![]() .故
.故
 .当且仅当
.当且仅当![]() ,即
,即![]() 时,等号成立.
时,等号成立.
所以(i)当![]() 时,
时,![]() (等号当且仅当
(等号当且仅当![]() 时成立).
时成立).
(ii)
当![]() 时,由
时,由![]() 得
得![]() ,
,
易证函数![]() 在
在![]() 上单调递增(证明过程略).
上单调递增(证明过程略).
所以,![]() .所以,
.所以,
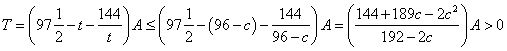 ,
,
即 .(等号当且仅当
.(等号当且仅当![]() 时取得)
时取得)
综上,若![]() ,则当日产量为88件时,可获得最大利润;若
,则当日产量为88件时,可获得最大利润;若![]() ,则当日产量为
,则当日产量为![]() 时,可获得最大利润.
时,可获得最大利润.
点评 分段函数是历年高考的热门话题,常考常新,值得我们在复课时认真对待.
例6 设二次函数![]() ,已知不论α,β为何实数,恒有
,已知不论α,β为何实数,恒有
![]()
(1)求证:![]()
(2)求证:![]()
(3)若函数![]() 的最大值为8,求b,c的值.
的最大值为8,求b,c的值.
讲解 (1)由![]() 产生b+c,只要消除差异
产生b+c,只要消除差异![]() ,这可令
,这可令![]()
![]()
![]()
从而知 ![]()
(2)由![]()
又因为![]()
(3)![]()
当![]()
由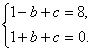 解得
解得 ![]()
点评 注意:![]() 且
且![]() , 这是用不等式证明等式的有效方法,很是值得重视.
, 这是用不等式证明等式的有效方法,很是值得重视.
例7 设f(x)=lg![]() ,a
,a![]() R, n
R, n![]() N且n
N且n![]() 2.若f(x)当x
2.若f(x)当x![]() (-
(-![]() ,1)有意义,求a的取值范围.
,1)有意义,求a的取值范围.
讲解 f(x)当x![]() (-
(-![]() ,1)有意义,当且仅当1+2
,1)有意义,当且仅当1+2![]() +…+(n-1)
+…+(n-1)![]() +an
+an![]() >0 对x
>0 对x![]() (-
(-![]() ,1)恒成立.即函数
,1)恒成立.即函数
g(x)=![]() +
+![]() +…+
+…+![]() +a>0
+a>0
对于任意的x![]() (-
(-![]() ,1)恒成立.
,1)恒成立.
因为g(x)在(-![]() ,1)上是减函数,其最小值为g(1)=
,1)上是减函数,其最小值为g(1)=
![]() +
+![]() +…+
+…+![]() +a=
+a=![]() (n-1)+a,
(n-1)+a,
所以g(x)
>0对x![]() (-
(-![]() ,1)恒成立的充要条件是
,1)恒成立的充要条件是![]() +a>0,即a>
+a>0,即a>![]() .
.
故所求实数a的范围为(![]() ,+
,+![]() ).
).
点评 构造函数是应用函数思想解题的基础,怎么构造,构造怎样的函数完全因题而定.请读者注意,恒成立问题在高考中多次出现,其解题方法,很值得探究.
例8 函数![]() 是定义在[0,1]上的增函数,满足
是定义在[0,1]上的增函数,满足![]() 且
且![]() ,在每个区间
,在每个区间![]() (
(![]() 1,2……)上,
1,2……)上,![]() 的图象都是斜率为同一常数k的直线的一部分.
的图象都是斜率为同一常数k的直线的一部分.
(1)![]() 及
及![]() ,
,![]() 的值,并归纳出
的值,并归纳出![]() 的表达式;
的表达式;
(2)直线![]() ,
,![]() ,x轴及
,x轴及![]() 的图象围成的矩形的面积为
的图象围成的矩形的面积为![]() (
(![]() 1,2……),记
1,2……),记![]() ,求
,求![]() 的表达式,并写出其定义域和最小值.
的表达式,并写出其定义域和最小值.
讲解 (1)为了求![]() ,只需在条件
,只需在条件![]() 中,令
中,令![]() ,即有
,即有
![]() ,得
,得![]() .
.
由![]() 及
及![]() ,得
,得![]() .
.
同理,![]() .
.
归纳得![]() .
.
(2)![]() 时,
时,
![]()
![]()
![]() .
.
故 ![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,
所以 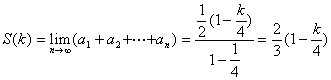 .
.
![]() 的定义域为
的定义域为![]() 1,当
1,当![]() 时取得最小值
时取得最小值![]() .
.
点评 本题是2004年北京高考数学第18题,将函数与数列综合在一起,体现了数学知识交汇性,是一道既知识、又考能力的活题.
l 针对性演练
1.合![]() ,若
,若![]() ,
,![]() ,则
,则![]() ,则运算
,则运算![]() 可能是 ( )
可能是 ( )
(A)加法 (B)减法 (C) 除法 (D)乘法
2.已知集合![]() ,
,![]() ,则满足条件
,则满足条件![]() 的映射
的映射![]() 的个数是 ( )
的个数是 ( )
(A)2 (B)4 (C)5 (D)7
3.某天清晨,小鹏同学生病了,体温上升,吃过药后感觉好多了,中午时他的体温基本正常,但是下午他的体温又开始上升,直到半夜才感觉身上不那么发烫了. 下面大致能上反映出小鹏这一天(0时—24时)体温的变化情况的图是
( )
 |
(A ) (B) (C) (D)
4.定义两种运算:![]()
![]() ,
,![]() ,则函数
,则函数![]() 为( )
为( )
(A)奇函数 (B)偶函数
(C)奇函数且为偶函数 (D)非奇函数且非偶函数
5.偶函数![]() 在
在![]() 上单调递增,则
上单调递增,则![]() 与
与![]() 的大小关系是 ( )
的大小关系是 ( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
6.已知函数![]()
![]() ,且正数C为常数.对于任意的
,且正数C为常数.对于任意的![]() ,存在一个
,存在一个![]() ,使
,使![]() ,则称函数
,则称函数![]() 在D上的均值为C. 试依据上述定义,写出一个均值为9的函数的例子:________________.
在D上的均值为C. 试依据上述定义,写出一个均值为9的函数的例子:________________.
7. 绿缘商店每月向工厂按出厂价每瓶3元购进一种饮料。根据以前的统计数据,若零售价定为每瓶4元,每月可销售400瓶;若每瓶售价每降低0.05元,则可多销售40瓶。请你给该商店设计一个方案:每月的进货量当月销售完,销售价应定为多少元和从工厂购进多少瓶时,才可获得最大的利润?
8.已知![]() 定义域为
定义域为![]() ,且对任意的
,且对任意的![]() 、
、![]() ,恒有
,恒有![]() ,
,![]() 时,
时,![]() .
.
(1)求![]() 的值,并证明
的值,并证明![]() ;
;
(2)求证:在![]() 的定义域内恒有
的定义域内恒有![]() .
.
9.已知定义域为[0,1]的函数f(x)同时满足:
(1)对于任意x∈[0,1],总有f(x)≥0;
(2)f(1)=1
(3)若![]() ,
,![]() ,
,![]() ,则有
,则有![]()
(Ⅰ)试求f(0)的值;
(Ⅱ)试求函数f(x)的最大值;
(Ⅲ)试证明:满足上述条件的函数f(x)对一切实数x,都有f(x)≤2x..
10. 设![]() 、
、![]() 为常数,
为常数,![]() :把平面上任意一点
:把平面上任意一点
(![]() ,
,![]() )映射为函数
)映射为函数![]()
(1)证明:不存在两个不同点对应于同一个函数;
(2)证明:当![]() 时,
时,![]() ,这里t为常数;
,这里t为常数;
(3)对于属于M的一个固定值![]() ,得
,得![]() ,在映射F的作用下,M1作为象,求其原象,并说明它是什么图象?
,在映射F的作用下,M1作为象,求其原象,并说明它是什么图象?
答案:
1.D.2.D.3.C.4.A.5.D.6.![]() ,
,![]() ,
, ![]() (
(![]() ).
).
7.450.8.略.
9.(I)令![]() ,
,
依条件(3)可得f(0+0) ≥f(0)+f(0),即f(0) ≤0.
又由条件(1)得f(0) ≥0,则f(0)=0.
(Ⅱ)任取![]() ,可知
,可知![]() ,
,
则![]() ,
,
即![]() ,故
,故![]()
于是当0≤x≤1时,有f(x)≤f(1)=1
因此,当x=1时,f(x)有最大值为1,
(Ⅲ)证明:
研究①当![]() 时,f(x) ≤1<2x
时,f(x) ≤1<2x
②当![]() 时,
时,
首先,f(2x) ≥f(x)+f(x)=2f(x),∴![]() .
.
显然,当![]() 时,
时,
![]() 成立.
成立.
假设当![]() 时,有
时,有![]() 成立,其中k=1,2,…
成立,其中k=1,2,…
那么当![]() 时,
时,
![]()
可知对于![]() ,总有
,总有![]() ,其中n=1,2,…
,其中n=1,2,…
而对于任意![]() ,存在正整数n,使得
,存在正整数n,使得![]() ,
,
此时![]() ,
,
③当x=0时,f(0)=0≤2x..
综上可知,满足条件的函数f(x),对x∈[0,1],总有f(x) ≤2x成立.
10. (1)假设有两个不同的点(![]() ,
,![]() ),(
),(![]() ,
,![]() )对应同一函数,即
)对应同一函数,即![]() 与
与![]() 相同,
相同,
即 ![]() 对一切实数x均成立。
对一切实数x均成立。
特别令x=0,得a=c;令![]() ,得b=d这与(a,b),(c,d)是两个不同点矛盾,假设不成立.
,得b=d这与(a,b),(c,d)是两个不同点矛盾,假设不成立.
故不存在两个不同点对应同函数。
(2)当![]() 时,可得常数a0,b0,使
时,可得常数a0,b0,使![]()
![]()
![]()
![]() 。
。
由于![]() 为常数,设
为常数,设![]() 是常数.
是常数.
从而![]() 。
。
(3)设![]() ,由此得
,由此得![]()
(![]() ,
,![]() )
)
在映射F下,![]() 的原象是(m,n),则M1的原象是
的原象是(m,n),则M1的原象是
![]()
消去t得![]() ,即在映射F下,M1的原象
,即在映射F下,M1的原象![]() 是以原点为圆心,
是以原点为圆心,![]() 为半径的圆.
为半径的圆.
第二讲 数列
陕西特级教师 安振平
l 高考风向标
数列的概念.等差数列及其通项公式、前n项和公式;等比数列及其通项公式、前n项和公式.数学归纳法及其应用.通项与前n项和之间的关系是高考常考的热点内容,递推数列在各地的高考中闪亮登场.
l 典型题选讲
例1 若数列{an}满足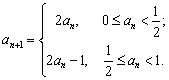 若
若![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
讲解 逐步计算,可得
![]() ,
,
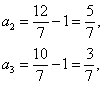
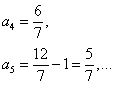
这说明数列{an}是周期数列,![]() 而
而![]() , 所以
, 所以![]() .应选B.
.应选B.
点评 分段数列问题是一种新问题,又涉及到周期数列,显示了以能力立意,题活而不难的特色.
例2 在等比数列{an}中,前n项和为Sn,若Sm,Sm+2,Sm+1成等差数列,则am, am+2, am+1成等差数列.
(1)写出这个命题的逆命题;
(2)判断逆命题是否为真,并给出证明.
讲解 (1)逆命题:在等比数列{an}中,前n项和为Sn,若am, am+2, am+1成等差数列,则 Sm,Sm+2,Sm+1成等差数列.
(2)设{an}的首项为a1,公比为q
由已知得2am+2= am
+ am+1
∴2a1qm+1=a1![]() +a1qm
+a1qm
∵a1≠0 q≠0 ,
∴2q2-q-1=0 ,
∴q=1或q=-![]() .
.
当q=1时,
∵Sm=ma1, Sm+2= (m+2)a1,Sm+1= (m+1)a1,
∴Sm+Sm+1≠2 Sm+2,
∴Sm,Sm+2,Sm+1不成等差数列.
当q=-![]() 时,
时,
2 Sm+2= ,
,
∴Sm+Sm+1=2 Sm+2 ,
∴Sm,Sm+2,Sm+1成等差数列.
综上得:当公比q=1时,逆命题为假;
当公比q≠1时,逆命题为真.
点评 对公比进行分类是本题解题的要害所在,问题好在分类,活在逆命题亦假亦真二者兼顾,可谓是一道以知识呈现、能力立意的新颖试题.
例3 设数列{an}前n的项和为 Sn,且![]() 其中m为常数,
其中m为常数,![]()
(1)求证:{an}是等比数列;
(2)若数列{an}的公比满足q=f(m)且 ,为等差数列,并求
,为等差数列,并求![]() .
.
讲解(1)由![]() ,得
,得
![]()
两式相减,得
![]()
![]()
![]() 是等比数列.
是等比数列.

点评 为了求数列![]() 的通项,用取"倒数"的技巧,得出数列
的通项,用取"倒数"的技巧,得出数列![]() 的递推公式,从而将其转化为等差数列的问题.
的递推公式,从而将其转化为等差数列的问题.
例4 设数列![]() 的前n项和为Sn,若
的前n项和为Sn,若![]() 是首项为S1各项均为正数且公比为q的等比数列.
是首项为S1各项均为正数且公比为q的等比数列.
(1)求数列![]() 的通项公式
的通项公式![]() (用S1和q表示);
(用S1和q表示);
(2)试比较![]() 的大小,并证明你的结论.
的大小,并证明你的结论.
讲解 (1)∵![]() 是各项均为正数的等比数列,
是各项均为正数的等比数列,
∴![]() .
.
当n=1时,a1=S1;
当![]() .
.
∴![]()
(2)当n=1时,
![]()
∴![]() .
.
![]()
![]()
∵![]()
①当q=1时,![]()
②当![]()
![]()
③当![]()
![]()
综上以上,我们可知:当n=1时,![]() .当
.当![]()
若![]() 若
若![]()
点评 数列与比较大小的综合是高考命题的一个老话题,我们可以找到较好的高考真题.本题求解当中用到![]() 与
与![]() 之间的关系式:
之间的关系式:
![]()
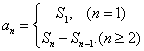
例5 已知数列![]() 满足
满足![]() >0,且对一切n∈N*,有
>0,且对一切n∈N*,有![]() ,
,
(1) 求证:对一切n∈N*,有![]() ;
;
(2) 求数列![]() 的通项公式;
的通项公式;
(3) 求证:![]() .
.
讲解 (1) 由 ![]() ①
①
得 ![]() ②
②
②-①得 ![]() =(Sn+1+Sn)(Sn+1-Sn)=(2
Sn+an+1) an+1
=(Sn+1+Sn)(Sn+1-Sn)=(2
Sn+an+1) an+1
∵ an+1 >0,
∴![]() .
.
(2)
由![]() ,得
,得
![]() (n≥2),
(n≥2),
两式相减,得
(an+1+ an)( an+1 - an)= an+1+ an,
∵an+1+ an >0,
∴an+1 - an =1.(n≥2)
当n=1,2时易得,a1=1,a2=2,∴an+1 - an =1(n≥1) .
从而{ an}是等差数列,其首项为a1=1,公差d=1,故an=n .
(3) ![]()
![]()
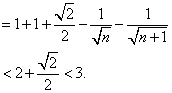
点评 关于数列不等式的证明,常用的技巧是放缩法,而放缩应特别注意其适度性,不可过大,也不可过小.
例6 如图,一粒子在区域![]() 上运动,在第一秒内它从原点运动到点
上运动,在第一秒内它从原点运动到点![]() ,接着按图中箭头所示方向在x轴、y轴及其平行方向上运动,且每秒移动一个单位长度.
,接着按图中箭头所示方向在x轴、y轴及其平行方向上运动,且每秒移动一个单位长度.
(1)设粒子从原点到达点![]() 时,所经过的时间分别为
时,所经过的时间分别为![]() ,试写出
,试写出![]() 的通相公式;
的通相公式;
(2)求粒子从原点运动到点![]() 时所需的时间;
时所需的时间;
(3)粒子从原点开始运动,求经过2004秒后,它所处的坐标.
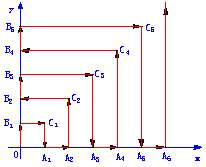 讲解 (1) 由图形可设
讲解 (1) 由图形可设![]() ,当粒子从原点到达
,当粒子从原点到达![]() 时,明显有
时,明显有
![]()
![]()
![]()
![]()
![]()
![]()
… …
![]()
![]()
∴![]() =
=![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
即![]() .
.
(2)有图形知,粒子从原点运动到点![]() 时所需的时间是到达点
时所需的时间是到达点![]() 所经过得时间
所经过得时间![]() 再加(44-16)=28秒,所以
再加(44-16)=28秒,所以![]() 秒.
秒.
(3)由![]()
![]() 2004,解得
2004,解得![]() ,取最大得n=44,
,取最大得n=44,
经计算,得![]() =1980<2004,从而粒子从原点开始运动,经过1980秒后到达点
=1980<2004,从而粒子从原点开始运动,经过1980秒后到达点![]() ,再向左运行24秒所到达的点的坐标为(20,44).
,再向左运行24秒所到达的点的坐标为(20,44).
点评 从起始项入手,逐步展开解题思维.由特殊到一般,探索出数列的递推关系式,这是解答数列问题一般方法,也是历年高考命题的热点所在.
例7 已知数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() .
.
(1)写出数列![]() 的前三项
的前三项![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)证明:对任意的整数![]() ,有
,有![]() .
.
讲解 (1)为了计算前三项![]() 的值,只要在递推式
的值,只要在递推式![]() 中,对
中,对![]() 取特殊值
取特殊值![]() ,就可以消除解题目标与题设条件之间的差异.
,就可以消除解题目标与题设条件之间的差异.
由![]()
由![]()
由![]()
(2)为了求出通项公式,应先消除条件式中的![]() .事实上
.事实上
当![]() 时,有
时,有
![]()
即有 ![]()
从而 ![]()
![]()
……
![]()
接下来,逐步迭代就有
![]()

经验证a1也满足上式,故知 ![]()
其实,将关系式![]() 和课本习题
和课本习题![]() 作联系,容易想到:这种差异的消除,只要对
作联系,容易想到:这种差异的消除,只要对![]() 的两边同除以
的两边同除以![]() ,便得
,便得
![]() .
.
令![]() 就有
就有
![]() ,
,
于是
![]() ,
,
这说明数列![]() 是等比数列,公比
是等比数列,公比![]() 首项
首项![]() ,从而,得
,从而,得
![]() ,
,
即 ![]() ,
,
故有![]()
(3)由通项公式得![]()
当![]() 且n为奇数时,
且n为奇数时, ![]()

当![]() 为偶数时,
为偶数时,![]()
![]()
![]()
当![]() 为奇数时,
为奇数时,![]() 为偶数,可以转化为上面的情景
为偶数,可以转化为上面的情景
![]()
故任意整数m>4,有![]()
点评 本小题2004年全国(旧教材版)高考理科压轴试题.主要考查数列的通项公式,等比数列的前n项和以及不等式的证明.考查灵活运用数学知识分析问题和解决问题的能力.当中的第2小题,显然与课本上的问题![]() 有着相同的本质.而第3小题又有着明显的高等数学的背景,体现了知识与技能的交汇,方法与能力的提升,显示了较强的选拔功能.
有着相同的本质.而第3小题又有着明显的高等数学的背景,体现了知识与技能的交汇,方法与能力的提升,显示了较强的选拔功能.
l 针对性演练
1 某人要买房,随着楼层的升高,上下楼耗费的精力增多,因此不满意度升高,当住第n层楼时,上下楼造成的不满意度为n,但高处空气清新,嘈杂音较小,环境较为安静,因此随楼层升高环境不满意度降低,设住第n层楼时,环境不满意度为![]() ,则此人应选( )
,则此人应选( )
(A) 1楼 (B) 2楼 (C) 3楼 (D) 4楼
2. 若等比数列的各项均为正数,前![]() 项之和为
项之和为![]() ,前
,前![]() 项之积为
项之积为![]() ,前
,前![]() 项倒数之和为
项倒数之和为![]() ,则
( )
,则
( )
(A)![]() =
=![]() (B)
(B)![]() >
>![]() (C)
(C)![]() (D)
(D)![]() >
>![]()
3. 2003年12月,全世界爆发"禽流感",科学家经过深入的研究,终于发现了一种细菌M在杀死"禽流感"病毒N的同时能够自身复制.已知1个细菌M可以杀死1个病毒N,并且生成2个细菌M,那么1个细菌M和2048个"禽流感"病毒N最多可生成细菌M的数值是 ( )
(A)1024 (B)2048 (C) 2049 (D)无法确定
4. 设数列![]() 的前n项和为
的前n项和为![]() ,令
,令![]() ,称
,称![]() 为数列
为数列![]() ,
,![]() ,……,
,……,![]() 的“理想数”,已知数列
的“理想数”,已知数列![]() ,
,![]() ,……,
,……,![]() 的“理想数”为2004,那么数列2,
的“理想数”为2004,那么数列2, ![]() ,
,![]() ,……,
,……,![]() 的“理想数”为
的“理想数”为
(A) 2002 (B) 2004 (C) 2006 (D) 2008
5. 某地为了防止水土流失,植树造林,绿化荒沙地,每年比上一年多植相同亩数的林木,但由于自然环境和人为因素的影响,每年都有相同亩数的土地沙化,具体情况为下表所示:
| 1998年 | 1999年 | 2000年 | |
| 新植亩数 | 1000 | 1400 | 1800 |
| 沙地亩数 | 25200 | 24000 | 22400 |
而一旦植完,则不会被沙化.
问:(1)每年沙化的亩数为多少?
(2)到那一年可绿化完全部荒沙地?
6. 已知正项数列![]() 满足
满足![]() (
(![]() ),且
),且![]() 求证
求证
(1)![]()
(2)![]()
答案
1.C 2. C 3.C 4.A
5.(1)由表知,每年比上一年多造林400亩.
因为1999年新植1400亩,故当年沙地应降为![]() 亩,但当年实际沙地面积为24000亩,所以1999年沙化土地为200亩.
亩,但当年实际沙地面积为24000亩,所以1999年沙化土地为200亩.
同理2000年沙化土地为200亩.
所以每年沙化的土地面积为200亩.
(2)由(1)知,每年林木的“有效面积”应比实造面积少200亩.
设2000年及其以后各年的造林亩数分别为![]() 、
、![]() 、
、![]() 、…,则n年造林面积总和为:
、…,则n年造林面积总和为:
![]() .
.
由题意:![]() 化简得
化简得
![]() ,
,
解得: ![]() .
.
故8年,即到2007年可绿化完全部沙地.
6.(1)将条件![]() 变形,得
变形,得![]() .
.
于是,有
![]()
![]()
![]()
…………
![]() .
.
将这n-1个不等式叠加,得 ![]()
故 ![]()
(2)注意到![]() ,于是由(1)得
,于是由(1)得
 ,
,
从而,有 ![]()
第三讲 三角函数
陕西特级教师 安振平
l 高考风向标
主要考查三角函数的定义,三角函数的符号,同角三角函数关系式及诱导公式,两角和与差的三角函数,二倍角的正弦、余弦、正切公式,三角函数的图象与性质,包括周期性、奇偶性、单调性、和最值性.
l 典型题选讲
例1 (1)已知:![]()
(2)已知:![]() 的值.
的值.


点评 三角问题的解决,变形是多途径的.例如:题1也可以逆向考虑,事实上


例2 已知电流I与时间t的关系式为![]() .
.
(1)右图是![]() (ω>0,
(ω>0,![]() )
)
在一个周期内的图象,根据图中数据求![]()
的解析式;
(2)如果t在任意一段![]() 秒的时间内,电流
秒的时间内,电流![]() 都能取得最大值和最小值,那么ω的最小正整数值是多少?
都能取得最大值和最小值,那么ω的最小正整数值是多少?
讲解 本小题主要考查三角函数的图象与性质等基础知识,考查运算能力和逻辑推理能力.
(1)由图可知 A=300.
设t1=-![]() ,t2=
,t2=![]() , 则周期T=2(t2-t1)=2(
, 则周期T=2(t2-t1)=2(![]() +
+![]() )=
)=![]() .
.
∴
ω=![]() =150π.
=150π.
又当t=![]() 时,I=0,即sin(150π·
时,I=0,即sin(150π·![]() +
+![]() )=0,
)=0,
而![]() , ∴
, ∴ ![]() =
=![]() .
.
故所求的解析式为![]() .
.
(2)依题意,周期T≤![]() ,即
,即![]() ≤
≤![]() ,(ω>0)
,(ω>0)
∴ ω≥300π>942,又ω∈N*,
故最小正整数ω=943.
点评 本题解答的开窍点是将图形语言转化为符号语言.其中,读图、识图、用图是形数结合的有效途径.
例3 已知函数![]() .
.
(1)求实数a,b的值;
(2)求函数![]() 的最大值及取得最大值时x的值.
的最大值及取得最大值时x的值.
(1)函数![]()
讲解 学会翻译,逐步展开解题思维.

![]() 时,函数f(x)的最大值为12.
时,函数f(x)的最大值为12.
点评 结论![]() 是历年高考命题的热点之一.
是历年高考命题的热点之一.
例4 已知tan2θ=-2,π<2θ<2π,求.
讲解
解题目标中含有角![]() ,可向
,可向![]() 角转化,以便出现
角转化,以便出现![]() ;而条件中的
;而条件中的![]() 可向
可向![]() 转化. 这样,就消除了解题目标与解题条件之间中的差异.事实上
转化. 这样,就消除了解题目标与解题条件之间中的差异.事实上
原式=
=
= ,
由 tan2θ=,
解得 tanθ=-或tanθ=,
∵π<2θ<2π,∴<θ<π,
∴tanθ=- ,
∴原式==3+2.
点评 差异分析,有时需要从条件和解题目标两个方向同时进行分析,这种相向而行的思维方式,可以快速联结解题的思维线路.
例5 在![]() 中,
中,![]() ,
,![]() ,
,![]() ,求
,求![]() 的值和
的值和![]() 的面积.
的面积.
讲解 本题是2004年北京高考试题,下面给出两种解法.
法一 先解三角方程,求出角A的值.
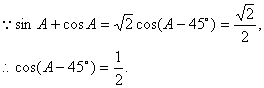
又![]() ,
,

![]()
![]() .
.
法二 由![]() 计算它的对偶关系式
计算它的对偶关系式![]() 的值.
的值.
![]() ①
①

![]() ,
,
![]() . ②
. ②
① + ② 得 ![]() .
.
① - ② 得 ![]() .
.
从而 ![]() .以下解法略去.
.以下解法略去.
点评 本小题主要考查三角恒等变形、三角形面积公式等基本知识,着重数学考查运算能力,是一道三角的基础试题.两种解法比较起来,你认为哪一种解法比较简单呢?
例6 设函数f(x)=a·b,其中向量a=(2cosx,1),b=(cosx, ![]() sin2x),x∈R.
sin2x),x∈R.
(1)若f(x)=1-![]() 且x∈[-
且x∈[-![]() ,
,![]() ],求x;
],求x;
(2)若函数y=2sin2x的图象按向量c=(m,n)(m<![]() )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.
讲解 (1)依题设可知,函数的解析式为
f(x)=a·b=2cos2x+![]() sin2x=1+2sin(2x+
sin2x=1+2sin(2x+![]() ).
).
由1+2sin(2x+![]() )=1-
)=1-![]() ,可得三角方程
,可得三角方程
sin(2 x
+![]() )=-
)=-![]() .
.
∵-![]() ≤x≤
≤x≤![]() ,
,
∴-![]() ≤2x+
≤2x+![]() ≤
≤![]() ,
,
∴2x+![]() =-
=-![]() ,即x=-
,即x=-![]() .
.
(2)函数y=2sin2x的图象按向量c=(m,n)平移后得到函数y=2sin2(x-m)+n的图象,即函数y=f(x)的图象.
由(1)得
f(x)=2sin2(x+![]() )+1.
)+1.
∵m<![]() ,∴
,∴![]() ,
,![]()
点评 本小题是2004年福建高考试题,主要考查平面向量的概念和计算,三角函数的恒等变换及其图象变换的基本技能,着重考查数学运算能力.平面向量与三角函数结合是高考命题的一个新的亮点之一.
例7 已知向量m=(1,1),向量n与向量m夹角为![]() ,且m·n=-1.
,且m·n=-1.
(1)求向量n;
(2)若向量n与向量q=(1,0)的夹角为![]() ,向量p=
,向量p=![]() ,其中A、C为△ABC的内角,且A、B、C依次成等差数列.求n+p的取值范围.
,其中A、C为△ABC的内角,且A、B、C依次成等差数列.求n+p的取值范围.
讲解 (1)设![]() ①
①
![]() 与
与![]() 夹角为
夹角为![]() ,有
,有![]() ·
·![]() =
=![]() ·
·![]() ·
·![]() ,
,![]() ②
②
由①②解得![]()
(2)由![]() 垂直知
垂直知![]() ,
,
由2B=A+C 知B=![]() ,A+C=
,A+C=![]()
若![]()
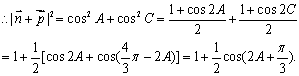
![]()
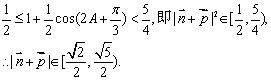
点评 本题的特色是将向量与三角综合,体现了知识的交汇性.解题后,请你反思:解题思维的入手点,解题思维的障碍点,解题思维的开窍点,只有这样的反思训练,请相信,你就会慢慢成为解题高手的.
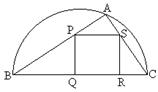
例8 如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余的地方种花.若BC=a,∠ABC=![]() ,设△ABC的面积为S1,正方形的面积为S2.
,设△ABC的面积为S1,正方形的面积为S2.
(1)用a,![]() 表示S1和S2;
表示S1和S2;
|
讲解 (1)∵![]()
∴![]()
设正方形边长为x.
则BQ=![]()
![]()
![]()
![]()
(2)当![]() 固定,
固定,![]() 变化时,
变化时,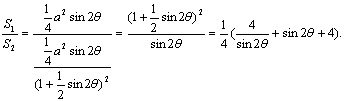
令![]()
![]() 令
令![]() 任取
任取![]() ,且
,且![]() ,
,
![]() .
.
![]() ,
,
![]() 是减函数.
是减函数.
![]() 取最小值,此时
取最小值,此时![]()
点评 三角函数有着广泛的应用,本题就是一个典型的范例.通过引入角度,将图形的语言转化为三角的符号语言,再通过局部的换元,又将问题转化为我们熟知的函数![]() .这些解题思维的拐点,你能否很快的想到呢?
.这些解题思维的拐点,你能否很快的想到呢?
l 针对性演练
1. 函数![]() 的图象如图所示,则
的图象如图所示,则![]() 的解析式可能是
( )
的解析式可能是
( )
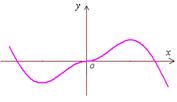 (A)
(A)![]()
(B)![]()
(C)![]()
(D)![]()
2.
已知![]() ,且
,且![]() ,则
,则![]() ( )
( )
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D) ![]()
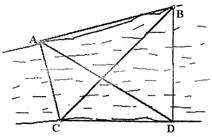
3. 如图,要测量河对岸A、B两点间的距离,今沿河岸选取相距40米的C、D两点,测得
∠ACB=60°,∠BCD=45°,∠ADB=60°,∠ADC=30°,则AB的距离是( ).
(A)20![]() (B)20
(B)20![]() (C)40
(C)40![]() (D)20
(D)20![]()
|
4.
设![]() 是某港口水的深度y(米)关于时间t(时)的函数,其中
是某港口水的深度y(米)关于时间t(时)的函数,其中![]() .下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
经长期观观察,函数![]() 的图象可以近似地看成函数
的图象可以近似地看成函数![]() 的图象.在下面的函数中,最能近似表示表中数据间对应关系的函数是 ( )
的图象.在下面的函数中,最能近似表示表中数据间对应关系的函数是 ( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
5.
已知![]() ,且
,且![]() 其中
其中![]() ,则关于
,则关于![]() 的值,在以下四个答案中,可能正确的是 ( )
的值,在以下四个答案中,可能正确的是 ( )
(A)![]() (B)3 或
(B)3 或![]()
(C)
![]() (D)
(D)![]() 或
或![]()
6.
如图,一个半径为10米的水轮按逆时针方向每分钟转4圈.记水轮上的点P到水面的距离为d米(P在水面下则d为负数),则d(米)与时间t(秒)之间满足关系式:![]() ,且当P点从水面上浮现时开始计算时间.有以下四个结论:
,且当P点从水面上浮现时开始计算时间.有以下四个结论:
①A=10; ②![]() ; ③
; ③![]() ; ④k=5.
; ④k=5.
则其中所有正确结论的序号是 .
7. 求函数![]() 的最小正周期和最小值;并写出该函数在
的最小正周期和最小值;并写出该函数在![]() 上的单调递增区间.
上的单调递增区间.
8.
求函数![]() 的最小正周期、最大值和最小值.
的最小正周期、最大值和最小值.
9.
已知α为锐角,且![]() 求
求![]() 的值.
的值.
10.
已知0<α<![]() ,tan
,tan![]() +cot
+cot![]() =
=![]() ,求sin(
,求sin(![]() )的值.
)的值.
11.
![]() .
.
12.
已知![]() 的值.
的值.
参考答案:
1.C. 2.A. 3.D. 4.A. 5.C. 6.①②④.
7.![]()

故该函数的最小正周期是![]() ;最小值是-2;单增区间是[
;最小值是-2;单增区间是[![]() ],
],![]() .
.
8. ![]()

所以函数f(x)的最小正周期是π,最大值是![]() ,最小值是
,最小值是![]() .
.
9. 原式=![]()
因为![]() 时,
时,![]()
所以 原式=![]()
因为α为锐角,由![]() 得
得![]()
所以 原式=![]()
10.由已知![]() .
.
![]()
从而 ![]()
![]() .
.
11.由![]()
于是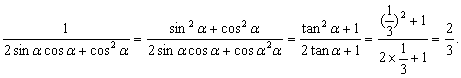
12.由已知得:![]()
![]() .
.
由已知条件可知![]()
从而 ![]() 有
有 ![]()
![]()
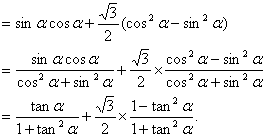
![]() ,得
,得
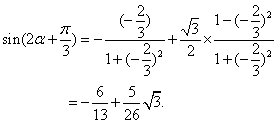
数学专题(五)
不 等 式
陕西 安振平
l 高考风向标
不等式的概念和性质,2元均值不等式.不等式的证明(比较法、分析法、综合法).不等式的解法(一元一次、一元二次、一元高次、分式、绝对值不等式)不等式的综合应用(求最值、求参数的取值范围、解答实际问题).
l 典型题选讲
例1 已知(![]() ,
,![]() )是直线
)是直线![]() 与圆
与圆![]() 的交点,则当
的交点,则当![]() 取最小值时,则实数
取最小值时,则实数![]() 的值等于( )
的值等于( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
讲解: 由交点满足方程,便得

对第1个等式两边平方后减去第2个等式,立即得出
![]() .
.
故当![]() 取最小值
取最小值![]() 时,实数
时,实数![]() 对于的值等于1,应该选C.
对于的值等于1,应该选C.
点评: 此题是一道解析几何面孔呈现的代数最值问题,解答中建立函数![]() ,而
,而![]() 是二次函数,其求最值的方法自然就想到了是配方法!
是二次函数,其求最值的方法自然就想到了是配方法!
例2 设不等式2x-1>m(x2-1)对满足m≤2的一切实数m的取值都成立,求x的取值范围.
讲解:令f(m)=2x-1-m(x2-1)=(1-x2)m+2x-1,可看成是一条直线(由m≤2知它实质是一条线段),且使m≤2的一切实数都有2x-1>m(x2-1)成立.
所以 ![]()
即 ![]()
即 
所以 ![]() .
.
点评:没有函数,构造函数,巧用线段函数的单调性质解题,这充分体现了函数思想在解答数学问题中的神奇作用.
例3 若![]() , 则函数
, 则函数![]() 的最大值是________.
的最大值是________.
讲解: 由对称性,可以猜想:当![]() 时,函数
时,函数![]() 取得最大值
取得最大值![]() .于是,就将求最值问题转化为不等式证明问题了.
.于是,就将求最值问题转化为不等式证明问题了.
令![]() ,
,![]() 则
则![]() 由
由![]() 得
得
![]()
![]() 于是
于是
![]()

这是显然成立的,
故当![]() 即
即![]() 时,
时,![]() 应填
应填![]()
点评:换元法的美妙之处在于将三角问题化归为代数问题,而猜想最值又将问题转化为不等式证明.应用分析法是证明不等式的有效方法之一,它可以化生为熟、化繁为简.
例4 某地区发生流行性病毒感染,居住在该地区的居民必须服用一种药物预防,规定每人每天早晚八时各服一片,现知该药片每片含药量为220毫克,若人的肾脏每12小时从体内滤出这种药的60%,在体内的残留量超过386毫克,就将产生副作用.
(1) 某人上午八时第一次服药,问到第二天上午八时服完药时,这种药在他体内还残留多少?
(2) 长期服用的人这种药会不会产生副作用?
讲解:(1)设人第![]() 次服药后,药在体内的残留量为
次服药后,药在体内的残留量为![]() 毫克.则
毫克.则![]() ,
,
![]() ,
,
(2)由![]() ,
,
![]() 是一个以数
是一个以数![]() 为首项,0.4为公比的等比数列,
为首项,0.4为公比的等比数列,
![]() ,
,
![]() ,
,
![]() 不会产生副作用.
不会产生副作用.
点评:本题是一道数列与不等式综合的应用性问题,它紧密结合人们的生活实际,是一道既考知识,又考能力的好问题.
例5 已知a>0,函数f(x)=ax-bx![]() .
.
(1) 当b>0时,若对任意x![]() R都有f(x)
R都有f(x)![]() 1,证明a
1,证明a![]() 2
2![]() ;
;
(2) 当b>1时,证明对任意x![]() [0,1],都有f(x)
[0,1],都有f(x)![]() 1的充要条件是b-1
1的充要条件是b-1![]() a
a![]() 2
2![]() ;
;
(3) 当0<b![]() 1时,讨论:对任意x
1时,讨论:对任意x![]() [0,1],都有f(x)
[0,1],都有f(x)![]() 1的充要条件.
1的充要条件.
讲解 (1) 对已知二次函数应用配方法,得
![]() ,当x
,当x![]() R时,f(x)
R时,f(x)![]() =
= ![]() ,
,
于是,对任意x![]() R都有f(x)
R都有f(x)![]() 1
1![]() f(x)
f(x)![]() =
= ![]()
![]() 1
1![]() a
a![]() 2
2![]() .
.
(2) 用f(x)![]() 、f(x)
、f(x)![]() 表示f(x)在[0,1]上的最大值、最小值,则对任意x
表示f(x)在[0,1]上的最大值、最小值,则对任意x![]() [0,1],都有f(x)
[0,1],都有f(x)![]() 1当且仅当
1当且仅当 (*)
(*)
而 f(x)=-b(x-![]() +
+![]() ,(x
,(x![]() [0,1])
[0,1])
当2b![]() 时,0<
时,0<![]()
![]() 1,f(x)
1,f(x)![]() =
= ![]() ,f(x)
,f(x)![]() =f(0)或f(1);
=f(0)或f(1);
当2b<a时,![]() >1, f(x)
>1, f(x)![]() = f(1),f(x)
= f(1),f(x)![]() =f(0).
=f(0).
于是
(*)![]()
 或
或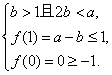
![]() b-1
b-1![]() a
a![]() 2
2![]() 或x
或x![]()
![]() b-1
b-1![]() a
a![]() 2
2![]() .
.
故对任意x![]() [0,1],都有f(x)
[0,1],都有f(x)![]() 1的充要条件是b-1
1的充要条件是b-1![]() a
a![]() 2
2![]() .
.
(3) 由(2)的解答知,对任意x![]() [0,1],都有f(x)
[0,1],都有f(x)![]() 1当且仅当
1当且仅当
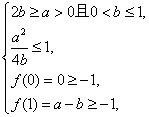 或
或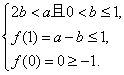
![]() 0<a
0<a![]() 2b或2b<a
2b或2b<a![]() b+1
b+1 ![]() 0<a
0<a![]() b+1.
b+1.
故当0<b![]() 1时,对任意x
1时,对任意x![]() [0,1],都有f(x)
[0,1],都有f(x)![]() 1的充要条件为0<a
1的充要条件为0<a![]() b+1.
b+1.
点评:含参数的二次函数与绝对值不等式相综合,这是历年高考命题的热点之一.读者在备考复习时,应当重视这类题型的解题技巧,掌握一些解题的套路,领悟当中的变化技能,反复思考参数的处理艺术.
例6(1)已知![]() 是正常数,
是正常数,![]() ,
,![]() ,求证:
,求证:![]() ,指出等号成立的条件;
,指出等号成立的条件;
(2)利用(1)的结论求函数![]() (
(![]() )的最小值,指出取最小值时
)的最小值,指出取最小值时![]() 的值.
的值.
讲解:(1)应用2元均值不等式,得
![]()
![]() ,
,
故 ![]() .
.
当且仅当![]() ,即
,即![]() 时上式取等号.
时上式取等号.
(2)由(1)![]() .
.
当且仅当![]() ,即
,即![]() 时上式取最小值,即
时上式取最小值,即![]() .
.
点评:给你一种解题工具,让你应用它来解答某一问题,这是近年考试命题的一种新颖的题型之一,很值得读者深刻反思和领悟当中的思维本质.
例7 如图,A、B为函数![]() 图像上两点,且AB∥x轴,点M(1,m)(m>3)是△ABC边AC的中点.
图像上两点,且AB∥x轴,点M(1,m)(m>3)是△ABC边AC的中点.
(1)设点B的横坐标为t,△ABC的面积为S,求S关于t的函数关系式![]() ;
;
(2)求函数![]() 的最大值,并求出相应的点C的坐标.
的最大值,并求出相应的点C的坐标.
讲解:先引如点A,B的坐标,再逐步展开解题思维.
(1)设B![]() ,A
,A![]() ,
,![]() ,M是△ABC边AC的中点,则
,M是△ABC边AC的中点,则
![]() ,
,
∴![]() .
.
(2)∵![]() ,M(1,m)是△ABC边AC的中点
,M(1,m)是△ABC边AC的中点
∴ 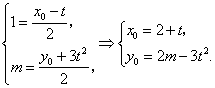
∴![]() .
.
当![]() 时,
时,
![]() .
.
当且仅当![]() ,即
,即![]() 时,S的最大值是
时,S的最大值是![]() ,此时点C的坐标是
,此时点C的坐标是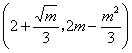 .
.
当m>9时,![]() 在区间(0,1)上是增函数,证明如下:
在区间(0,1)上是增函数,证明如下:
设![]() .
.
∵![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 在(0,1)上为增函数,
在(0,1)上为增函数,
故![]() 时,
时,![]() ,此时
,此时![]() .
.
点评:本题是笔者自编的一道试题,曾作为陕西省高三的会考试题.此题的解答如果改为应用导数知识,其解法就要简洁的多了,请读者不妨一试.
例8 过点![]() 作曲线
作曲线![]() (
(![]() ,
,![]() ,
,![]() )的切线切点为
)的切线切点为![]() ,设
,设![]() 点在
点在![]() 轴上的投影是点
轴上的投影是点![]() ;又过点
;又过点![]() 作曲线
作曲线![]() 的切线切点为
的切线切点为![]() ,设
,设![]() 点在
点在![]() 轴上的投影是点
轴上的投影是点![]() ;……;依此下去,得到一系列点
;……;依此下去,得到一系列点![]() ,设点
,设点![]() 的横坐标是
的横坐标是![]() .
.
(1)求证:![]() ,
,![]() ;
;
(2)求证:![]() ;
;
(3)求证:![]() (注:
(注:![]() ).
).
讲解:(1)对![]() 求导数,得
求导数,得![]() .
.
若切点是![]() ,则切线方程是
,则切线方程是![]() .
.
当![]() 时,切线过点
时,切线过点![]() ,即
,即![]() ,得
,得![]() ;
;
当![]() 时,切线过点
时,切线过点![]() ,即
,即![]() ,得
,得![]() .
.
所以数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,
的等比数列,![]() ,
,![]() .
.
(2)应用二项式定理,得
![]()
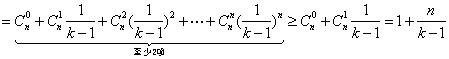 .
.
(3)记![]() ,则
,则![]() ,
,
两式相减,得
![]() ,
,
 ,
,
故 ![]() .
.
点评:本题综合解析几何、导数、数列、二项式定理、不等式等知识点,在解答时,需要较强的思维能力和排除万难的吃苦精神.
l 针对性演练
1.
已知![]() 是正实数,则不等式组
是正实数,则不等式组![]() 是不等式组
是不等式组![]() 成立的( )
成立的( )
(A)充分不必要条件 (B) 必要不充分条件
(C) 充分且必要条件 (D) 既不充分又不必要条件
2. 若a,b![]() 则a <1,b<1,是a+b+a-b<2成立的
(
)
则a <1,b<1,是a+b+a-b<2成立的
(
)
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
3. 已知不等式m2+(cos2θ-5)m+4sin2θ≥0恒成立,则实数m的取值范围是
(A)0≤m≤4 (B)1≤m≤4
(C)m≥4或x≤0 (D)m≥1或m≤0
4.若对任意的长方体![]() ,都存在一个与
,都存在一个与![]() 等高的长方体
等高的长方体![]() ,使得
,使得![]() 与
与![]() 的侧面积之比和体积之比都等于
的侧面积之比和体积之比都等于![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
5.不等式x2-x-6>3-x的解集是( )
(A)(3,+∞) (B)(-∞,-3)∪(3,+∞)
(C)(-∞,-3)∪(-1,+∞) (D)(-∞,-3)∪(-1,3)∪(3,+∞)
6.是否存在常数![]() ,使得不等式
,使得不等式![]() 对任意正实数
对任意正实数![]() 、
、![]() 恒成立?证明你的结论.
恒成立?证明你的结论.
7. 已知![]()
(1)当![]() 时,若函数f (x)的图象与直线
时,若函数f (x)的图象与直线![]() 均无公共点,求证
均无公共点,求证![]()
(2)![]() 对于给定的负数
对于给定的负数![]() ,有一个最大的正数M(a),使得
,有一个最大的正数M(a),使得![]() ,问a为何值时,M(a)最大,并求出这个最大值M(a),证明你的结论.
,问a为何值时,M(a)最大,并求出这个最大值M(a),证明你的结论.
8. 设![]() 为正实数,满足
为正实数,满足
![]()
求![]() 的最大值.
的最大值.
9. 已知函数![]()
![]() .
.
(1)证明函数![]() 的图象关于点(a,-1)成中心对称图形;
的图象关于点(a,-1)成中心对称图形;
(2)当![]() ,
,![]() 时,求证:
时,求证:![]() ,
,![]() ;
;
(3)我们利用函数![]() 构造一个数列
构造一个数列![]() ,方法如下:对于给定的定义域中的
,方法如下:对于给定的定义域中的![]() ,令
,令![]() ,
,![]() ,…,
,…,![]() ,…,在上述构造数列的过程中,如果
,…,在上述构造数列的过程中,如果![]() (i=2,3,4,…)在定义域中,构造数列的过程将继续下去;如果
(i=2,3,4,…)在定义域中,构造数列的过程将继续下去;如果![]() 不在定义域中,构造数列的过程停止.
不在定义域中,构造数列的过程停止.
①如果可以用上述方法构造出一个常数列![]() ,求实数a的取值范围;
,求实数a的取值范围;
②如果取定义域中任一值作为![]() ,都可以用上述方法构造出一个无穷数列
,都可以用上述方法构造出一个无穷数列![]() ,求实数a的值.
,求实数a的值.
参考答案:
1.B.2.C.3.C.4.D.5.D.
6.当![]() 时,由已知不等式得
时,由已知不等式得![]() .
.
下面分两部分给出证明:
⑴先证![]() ,
,
此不等式![]()
![]()
![]() ,此式显然成立;
,此式显然成立;
⑵再证![]() ,
,
此不等式![]()
![]()
![]() ,此式显然成立.
,此式显然成立.
综上可知,存在常数![]() ,是对任意的整数x、y,题中的不等式成立.
,是对任意的整数x、y,题中的不等式成立.
7. (1)![]() 的图象与y=x无公共点.
的图象与y=x无公共点.

(2)

8.令
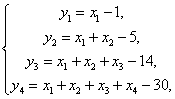
则 ![]() ,
,
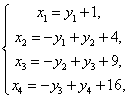
于是 ![]()
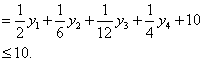
当 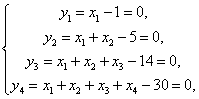 即
即![]() 时,
时,![]()
9.(1)设点P(![]() ,
,![]() )是函数
)是函数![]() 图象上一点,则
图象上一点,则![]() ,
,
点P关于(a,-1)的对称点![]() ,
,![]() .
.
∵![]() ,
,
![]() ,
,
∴![]() ,即点
,即点![]() 在函数
在函数![]() 的图象上,
的图象上,
∴函数![]() 的图象关于点(a,-1)成中心对称图形.
的图象关于点(a,-1)成中心对称图形.
(2)∵![]()
![]() .
.
又![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∴![]() .
.
(3)①根据题意,只需x≠a时,![]() 有实解,即
有实解,即![]() 有实解,即
有实解,即![]() 有不等于a的解,
有不等于a的解,
∴![]()
由![]() 得:a≤-3或a≥1,
得:a≤-3或a≥1,
由![]()
![]() .
.
综上a≤-3或a≥1;
②根据题意,应满足![]() 时
时![]() 无实解,
无实解,
即![]() 时
时![]() 无实解,
无实解,
由于![]() 不是方程
不是方程![]() 的解,
的解,
∴对于任意![]() ,
,![]() 无解,
无解,
∴a=-1.
数学专题(六)
直线与圆锥曲线
陕西 安振平
l 高考风向标
直线的倾斜角和斜率,直线的方程,两直线的位置关系,简单的线性规划.圆的方程,椭圆、双曲线、抛物线的定义、方程和简单的几何性质,直线与圆锥曲线的位置关系.将解析几何知识和向量知识综合于一题,这是近年高考数学命题的一个新的亮点.
l 典型题选讲
例1 若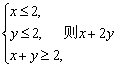 的取值范围是( ).
的取值范围是( ).
A. [2,6] B. [2,5] C.[3,6] D.[3,5]
讲解 由![]() 得
得 ![]() 又
又![]() 所以当
所以当![]() 时,原不等式组成立,从而
时,原不等式组成立,从而![]() 故应选A.
故应选A.
点评 请读者不妨画个图形,可以给出图形解法吗?
例2 椭圆![]() 的两个焦点为F1、F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则
的两个焦点为F1、F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.4
D.4
讲解 由椭圆的方程可以读出 ![]() ,则
,则 ![]() . 令
. 令![]() ,则点P的横坐标
,则点P的横坐标![]() ,代入椭圆方程
,代入椭圆方程![]() ,解得,点P的纵坐标
,解得,点P的纵坐标![]() . 而
. 而![]() ,于是,在Rt△PF1F2中,应用勾股定理,得
,于是,在Rt△PF1F2中,应用勾股定理,得
![]() .应选C.
.应选C.
点评 请读者自己画出图形. 当然,不必画图,图在心中也能解题.
例3 设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l的斜率的取值范围是( )
A.[-![]() ,
,![]() ] B.[-2,2] C.[-1,1] D.[-4,4]
] B.[-2,2] C.[-1,1] D.[-4,4]
讲解 易知抛物线![]() 的准线
的准线![]() 与x轴的交点为Q (-2 ,
0),于是,可设过点Q (-2
, 0)的直线
与x轴的交点为Q (-2 ,
0),于是,可设过点Q (-2
, 0)的直线![]() 的方程为
的方程为![]() ,
,
联立
其判别式为![]() ,可解得
,可解得 ![]() ,应选C.
,应选C.
点评 对斜率取特殊值也可巧解;如果画图形,可以看出答案吗?.
例4 设双曲线![]() 与直线
与直线![]() 相交于两个不同的点A、B.
相交于两个不同的点A、B.
(1)
双曲线C的离心率![]() 的取值范围;
的取值范围;
(2)
直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
讲解:(1)由C与t相交于两个不同的点,故知方程组

有两个不同的实数解.消去y并整理得
(1-a2)x2+2a2x-2a2=0. ①

双曲线的离心率

(2)设![]()

由于x1+x2都是方程①的根,且1-a2≠0,
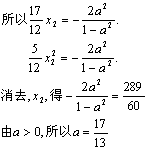
点评 本小题主要考查直线和双曲线的概念和性质,平面向量的运算等解析几何的基本思想和综合解题能力.
例5 某人承揽一项业务:需做文字标牌2个,绘画标牌3个。现有两种规格的原料,甲种规格每张3![]() ,可做文字标牌1个、绘画标牌2个;乙种规格每张2
,可做文字标牌1个、绘画标牌2个;乙种规格每张2![]() ,可做文字标牌2个、绘画标牌1个.求这两种规格的原料用多少张才能使总的用料面积最小?
,可做文字标牌2个、绘画标牌1个.求这两种规格的原料用多少张才能使总的用料面积最小?
讲解 设用甲种规格原料x 张,乙种规格原料y张,则可做文字标牌x+2y个,绘画标牌2x+y个.由题意可得
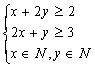 ,
,
 所用原材料的总面积
所用原材料的总面积![]() ,作出可行域如图示阴影部分内的整点,作直线
,作出可行域如图示阴影部分内的整点,作直线![]() ,作一组与直线
,作一组与直线![]() 平行的直线
平行的直线![]() .
.
当直线![]() 通过2x+y=3与直线x+2y=2的交点
通过2x+y=3与直线x+2y=2的交点![]() 时,t取得最小值
时,t取得最小值![]()
因为![]() 不是整点,所以它不是最优解.当
不是整点,所以它不是最优解.当![]() 时,
时,![]()
可知当![]() 时,
时,![]() 代入约束条件,可得
代入约束条件,可得![]() ,即经过可行域内的整点,点B(1,1)满足3x+2y=5,使t最小,所以最优解为B(1,1).
,即经过可行域内的整点,点B(1,1)满足3x+2y=5,使t最小,所以最优解为B(1,1).
故用甲种规格的原料1张,乙种规格的原料1张,能使总的用料面积最小,其最小值是5![]() .
.
点评 求整点最优解时,可先转化为普通线性规划求解.若所求得的最优解不是整点时,再借助不定方程的知识调整最优值,最后求出整点最优解.因为在考试时,常需要作出一些图形,而要解决作图的准确性问题,就必须抓住图形中的一些关键点和图形的变化趋势.只有抓住了局部的关键点,也就带动了整体的图形状态.
例6 已知椭圆C的中心在原点,焦点F1、F2在x轴上,点P为椭圆上的一个动点,且∠F1PF2的最大值为90°,直线l过左焦点F1与椭圆交于A、B两点,△ABF2的面积最大值为12.
(1)求椭圆C的离心率;
(2)求椭圆C的方程.
讲解 (1)设![]() .由
.由

得 ![]() .
.
(2) 1) 当k存在时,设l的方程为 ![]() ………………①
………………①
椭圆方程为![]() .
.
由![]() 得
得 ![]() .
.
于是椭圆方程可化为 ![]() ………………②
………………②
把①代入②,得
![]() ,
,
整理得
![]() ,
,
则x1、x2是上述方程的两根,且
![]() ,
,
![]() .
.
AB边上的高![]()
![]()
 .
.
2)当k不存在时,把直线![]() 代入椭圆方程,得
代入椭圆方程,得
![]()
由①②知S的最大值为![]() .由题意得
.由题意得![]() =12 所以
=12 所以![]() ,
,![]() .
.
所以面积最大时椭圆方程为:![]()
点评 也可这样求解:![]()
![]() .
.
例7 经过抛物线y![]() 的焦点F的直线L与该抛物线交于A,B两点.
的焦点F的直线L与该抛物线交于A,B两点.
(1) 线段AB的斜率为k,试求中点M的轨迹方程;
(2) 直线的斜率k>2,且点M到直线3 x+4y+m=0的距离为![]() ,试确定m的取值范围.
,试确定m的取值范围.
讲解 (1) 设A(![]() 直线AB的方程为y=k(x-1) (k≠0),代入
直线AB的方程为y=k(x-1) (k≠0),代入![]() 得
得
k![]() x
x![]() -(2k
-(2k![]() +4)x+k
+4)x+k![]() =0.
=0.
设M(x ,y),则

∴点M的坐标为(![]() .
.
于是消去k,可得M的轨迹方程为![]() .
.
(2) 由于
d=
所以
![]()
即
0<![]() <
<![]() , 得
, 得
0<![]() ,
,
即 ![]() 或
或 ![]()
故实数![]() 的取值范围为
的取值范围为 ![]() .
.
点评 圆锥曲线的焦点弦问题是历年高考的热门话题,解答过程当中有一些需要我们掌握的技巧和方法,应当引起读者深刻的反思.
例8 已知动点![]() 与双曲线
与双曲线![]() 的两个焦点
的两个焦点![]() 、
、![]() 的距离之和为定值,且
的距离之和为定值,且![]()
![]() 的最小值为
的最小值为![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)若已知![]() ,
,![]() 、
、![]() 在动点
在动点![]() 的轨迹上且
的轨迹上且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
讲解 (1)由题意![]() .设
.设![]() (
(![]() ),由余弦定理, 得
),由余弦定理, 得
![]() .
.
又![]() ·
·![]() ,
,
当且仅当![]() 时,
时,![]() ·
·![]() 取最大值,
取最大值,
此时![]() 取最小值
取最小值![]() ,令
,令![]() ,
,
解得![]() ,
,![]() ,∴
,∴![]() ,
,
故所求![]() 的轨迹方程为
的轨迹方程为![]() .
.
(2)设![]() ,
,![]() ,则由
,则由![]() ,可得
,可得
![]() ,
,
故![]() .
.
∵![]() 、
、![]() 在动点
在动点![]() 的轨迹上,
的轨迹上,
![]()
![]() 且
且![]() ,
,
消去![]() 可得
可得![]() ,解得
,解得
![]() ,
,
又![]() ,∴
,∴![]() ,解得
,解得![]() ,
,
故实数![]() 的取值范围是
的取值范围是![]() .
.
点评 为了求参数的取值范围,只要列出关于参数的不等式,而建立不等式的方法有多种方法,诸如:判别式法、均值不等式法、有界性法等等.新教材的高考已经进行了5年,而解析几何解答试题和向量综合呈现了新高考的崭新亮点,体现了向量知识的工具性和广泛的应用性.
l 针对性演练
1.直线![]() 与直线
与直线![]() 平行且不重合,则a等于( )
平行且不重合,则a等于( )
A ![]() B
B ![]() C 0或
C 0或![]() D. 0或
D. 0或![]()
2.椭圆的焦点为![]() ,过点
,过点![]() 作直线与椭圆相交,被椭圆截得的最短的线段MN长为
作直线与椭圆相交,被椭圆截得的最短的线段MN长为![]() ,
,![]() 的周长为20,则椭圆的离心率为( )
的周长为20,则椭圆的离心率为( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
3.若P为抛物线![]() 上任意一点,以P为圆心且与
上任意一点,以P为圆心且与![]() 轴相切的圆必过定点M,则点M的坐标是( ).
轴相切的圆必过定点M,则点M的坐标是( ).
A ![]() B
B
![]() C
C ![]() D
D ![]()
4.已知抛物线![]() 的焦点为,过
的焦点为,过![]() 作两条互相垂直的弦
作两条互相垂直的弦![]() 、
、![]() ,设
,设![]() 、
、![]() 的中点分别为
的中点分别为![]() .
.
(1) 求证:直线![]() 必过定点;
必过定点;
(2)分别以![]() 和
和![]() 为直径作圆,求两圆相交弦中点
为直径作圆,求两圆相交弦中点![]() 的轨迹方程.
的轨迹方程.
5.设![]() 是单位圆
是单位圆![]() 的直径,
的直径,![]() 是圆上的动点,过点
是圆上的动点,过点![]() 的切线与过点
的切线与过点![]() 的切线分别交于
的切线分别交于![]() 两点. 四边形
两点. 四边形![]() 的对角线
的对角线![]() 和
和![]() 的交点为
的交点为![]() ,求
,求![]() 的轨迹.
的轨迹.

6.
椭圆的两焦点分别为![]() 、
、![]() ,直线
,直线![]() 是椭圆的一条准线.
是椭圆的一条准线.
(1)求椭圆的方程;
 (2)设点
(2)设点![]() 在椭圆上,且
在椭圆上,且![]() ,求
,求 的最大值和最小值.
的最大值和最小值.
7. 在△ABC中,sinA、sinB、sinC构成公差为正的等差数列,且其周长为12.以![]() 为x轴,AC的中垂线为y轴建立直角坐标系xoy.
为x轴,AC的中垂线为y轴建立直角坐标系xoy.
(1)证明存在两个定点E、F,使得BE+BF为定长;并求出点E、F的坐标及点B的轨迹Γ;
(2)设P为轨迹Γ上的任一点,点M、N分别在射线PA、PC上,动点Q满足![]() ,经过点A且以
,经过点A且以![]() 为方向向量的直线与动点Q的轨迹交于点R,试问:是否存在一个定点D,使得
为方向向量的直线与动点Q的轨迹交于点R,试问:是否存在一个定点D,使得![]() 为定值?若存在,求出点D的坐标;若不存在,说明理由?
为定值?若存在,求出点D的坐标;若不存在,说明理由?
8.已知A(-2,0),B(2,0),动点P与A、B两点连线的斜率分别为![]() 和
和![]() ,且满足
,且满足![]() ·
·![]() =t (t≠0且t≠-1).
=t (t≠0且t≠-1).
(1)求动点P的轨迹C的方程;
(2)当t<0时,曲线C的两焦点为F1,F2,若曲线C上存在点Q使得∠F1QF2=120O,
求t的取值范围.
答案
1.D 2.B 3.A
4.(1)由题可知![]() ,设
,设![]() ,
,![]() ,直线AB的方程为
,直线AB的方程为![]() ,
,
则

(1)—(2)得![]() ,即
,即![]() ,代入方程
,代入方程![]() ,解得
,解得
![]()
同理可得:![]() 的坐标为
的坐标为![]() .
.
直线![]() 的斜率为
的斜率为![]() ,方程为
,方程为![]() ,
,
整理得![]() ,
,
显然,不论![]() 为何值,
为何值,![]() 均满足方程,
均满足方程,
所以直线![]() 恒过定点
恒过定点![]()
![]() .
.
(2)过![]() 作准线
作准线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() . 由抛物线的性质不难知道:准线
. 由抛物线的性质不难知道:准线![]() 为圆
为圆![]() 与圆
与圆![]() 的公切线.
的公切线.
设两圆的相交弦交公切线于点![]() ,则由平面几何的知识可知:
,则由平面几何的知识可知:![]() 为
为![]() 的中点. 所以
的中点. 所以
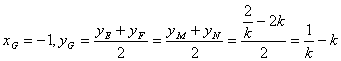 ,
,
即 ![]() .
.
又因为公共弦必与两圆的连心线垂直,所以公共弦的斜率为
![]() ,
,
所以,公共弦所在直线的方程为 ![]() ,
,
即 ![]() ,
,
所以公共弦恒过原点.
根据平面几何的知识知道:公共弦中点就是公共弦与两圆连心线的交点,所以原点![]() 、定点
、定点![]()
![]() 、所求点构成以
、所求点构成以![]() 为直角顶点的直角三角形,即
为直角顶点的直角三角形,即![]() 在以
在以![]() 为直径的圆上.
为直径的圆上.
5.以圆心O为原点,直径![]() 为x轴建立直角坐标系,则A(-1,0),B(1,0),单位圆的方程为
为x轴建立直角坐标系,则A(-1,0),B(1,0),单位圆的方程为![]() 设 N的坐标为
设 N的坐标为![]() ,则切线DC的方程为:
,则切线DC的方程为:![]() ,
,
 由此可得
由此可得![]()
AC的方程为
![]()
BD的方程为
![]()
将两式相乘得:![]() ,即
,即![]()
当点N恰为A或B时,四边形![]() 变为线段AB,这不符合题意,所以轨迹不能包括A、B两点,所以
变为线段AB,这不符合题意,所以轨迹不能包括A、B两点,所以![]() 的轨迹方程为
的轨迹方程为![]() ,(
,(![]() ).
).
6. (1)设椭圆的方程为![]() ,则由
,则由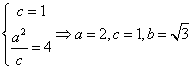 ,椭圆方程为
,椭圆方程为![]() .
.
(2)因为![]() 在椭圆上,故
在椭圆上,故

 .
.
由平面几何知识![]() ,即
,即![]() ,所以
,所以![]() .
.
记![]() ,设
,设![]() 且
且![]() ,则
,则
![]() ,
,
所以![]() 在
在![]() 上单调递减,于是,当
上单调递减,于是,当![]() 时原式取最大值
时原式取最大值![]() ,当
,当![]() 时,原式取最小值
时,原式取最小值![]() .
.
7.(1)由sinA、sinB、sinC构成公差为正的等差数列,得
a+c=2b,且a>b>c.
因a+b+c=12,故a+c=8,即BC+BA=8为定值.
注意到8>AC=4,且BC>BA,
故B的轨迹是以A、C为焦点,8为长轴长,在y轴左侧且除去顶点的椭圆的一部分.
并且存在定点E、F,它们分别为A、C,从而它们的坐标分别为(-2,0),(2,0).
 (2)如图所示,不妨取
(2)如图所示,不妨取![]() ,则以PMN为顶点可作出一个菱形PMTN,于是
,则以PMN为顶点可作出一个菱形PMTN,于是![]() ,
,![]() ,且
,且![]() ,从而PQ为∠APC的外角∠SPA的平分线.过A且以
,从而PQ为∠APC的外角∠SPA的平分线.过A且以![]() 为方向向量的直线AS⊥PQ.
为方向向量的直线AS⊥PQ.
从而![]() ,于是只须取AC的中点为D(O),即有
,于是只须取AC的中点为D(O),即有![]() =4为定值.故存在定点D,而
=4为定值.故存在定点D,而![]() 为定值.
为定值.
8.(1) 设点P坐标为(x,y),依题意得![]() =t
=t![]() y2=t(x2-4)
y2=t(x2-4)![]()
![]() +
+![]() =1
=1
轨迹C的方程为![]() +
+![]() =1(x≠
=1(x≠![]() 2).
2).
(2) 当-1<t<0时,曲线C为焦点在x轴上的椭圆,
设![]() =r1,
=r1,![]() = r2, 则r1+ r2=2a=4.
= r2, 则r1+ r2=2a=4.
在△F1PF2中,![]() =2c=4
=2c=4![]() ,
,
∵∠F1PF2=120O,由余弦定理,
得4c2=r![]() +r
+r![]() -2r1r2
-2r1r2![]() = r
= r![]() +r
+r![]() + r1r2
+ r1r2
= (r1+r2)2-r1r2≥(r1+r2)2-(![]() )2=3a2, ∴16(1+t)≥12, ∴t≥-
)2=3a2, ∴16(1+t)≥12, ∴t≥-![]() .
.
所以当-![]() ≤t<0时,曲线上存在点Q使∠F1QF2=120O
≤t<0时,曲线上存在点Q使∠F1QF2=120O
当t<-1时,曲线C为焦点在y轴上的椭圆,
设![]() =r1,
=r1,![]() = r2,则r1+r2=2a=-4 t,
= r2,则r1+r2=2a=-4 t,
在△F1PF2中, ![]() =2c=4
=2c=4![]() .
.
∵∠F1PF2=120O,由余弦定理,得
4c2=r![]() +r
+r![]() -2r1r2
-2r1r2![]() = r
= r![]() +r
+r![]() + r1r2= (r1+r2)2-r1r2≥(r1+r2)2-(
+ r1r2= (r1+r2)2-r1r2≥(r1+r2)2-(![]() )2=3a2,
)2=3a2,
∴16(-1-t)≥-12t![]() t≤-4.
t≤-4.
所以当t≤-4时,曲线上存在点Q使∠F1QF2=120O
综上知当t<0时,曲线上存在点Q使∠AQB=120O的t的取值范围是![]() .
.