数学试题
填空题集锦
陕西特级教师 安振平
1
在某次数学考试中，学号为
的同学的考试成绩
，
且满足
，则这四位同学的考试成绩的所有可能情况有 15
种．
2 一同学在电脑中打出如下若干个圆（图中●表示实圆，○表示空心圆）：
●○●●○●●●○●●●●○●●●●●○●●●●●●○
若将此若干个圆依次复制得到一系列圆，那么在前2002个圆中，有 445 个空心圆．
3 甲离学校10公里，乙离学校a公里，其中乙离甲3公里，则实数a的取值范围为___[7，13]_________.
4 设K是由函数y=f(x)上任意两点连线的斜率组成的集合.试写出K是区间（0，1）时的
一个函数 
等等.
（写出一个函数即可，不必考虑全部）.
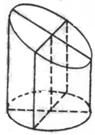
5 一圆柱被一平面所截，截口是一个椭圆．已知椭圆的长轴长为5，短轴长为4，被截后几何体的最短侧面母线长为1，则该几何体的体积等于 10π ．
6
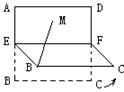
正方形ABCD的边长是2，E、F分别是AB和CD的中点，将正方形沿EF折成直二面角（如图所示）．M为矩形AEFD内的一点，如果ÐMBE=ÐMBC，MB和平面BCF所成角的正切值为1/2，那么点M到直线EF的距离为__
/2______．
7 对于任意两个复数z1=x1+y1i，z2=x2+y2i（x1、y1、x2、y2为实数），定义运算⊙为：
z1⊙z2=x1x2+y1y2．设非零复数w1、w2在复平面内对应的点分别为P1、P2，点为O为坐标原点．如果w1⊙w2=0，那么在DP1OP2中，ÐP1OP2的大小为_p/2._______．
8
用a克的某种溶质配制一定浓度的b克溶液(0＜a＜b)，若将其溶质减少m克(0＜m＜a)，会使溶液的浓度降低；而将其溶质增加m克，会使溶液的浓度增大.请根据这一现象提炼出一个不等式： ______
_______.
9
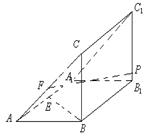
如图，在直三棱柱
中，
，
，E、F分别是
、AC的中点，P是
上任一点，则异面直线BE与PF所成角的大小为 ___
_____.
10 将抛物线
的内接正三角形
（O为坐标原点）绕y轴旋转一周得到一个几何体，则此几何体的体积为_
______.
11 若方程
=1表示椭圆或双曲线，则其焦距等于 2
.
12 设f(x)＝，利用课本中推导等差数列前n项和的公式的方法，可求得f(－5)＋f(－4)＋……＋f(0)＋……＋f(5)＋f(6)的值为 3 .
13
直角三角板在平面
上的射影可以是_②③④⑤ ______(写出所有你认为可能情况的序号)．
①一点 ② 线段 ③ 直角三角形
④锐角三角形 ⑤钝角三角形
14 已知函数
，则使得
恒成立的最小正整数
的值
为 2 。
15 若一个圆锥中有三条母线两两互相垂直，则此圆锥的侧面展开图的圆心角为 
16
圆心在抛物线y2＝2x上，且与x轴和该抛物线的准线都相切的一个圆的方程是_(x－
)2＋( y±1)2＝1______．(写一个即可)
17 
的图象与
轴有交点，则实数
的取值范围是 
.
18 小宁中午放学回家自己煮面条吃．有下面几道工序：①洗锅盛水2分钟；②洗菜6分钟；③准备面条及佐料2分钟；④用锅把水烧开10分钟；⑤煮面条和菜3分钟．以上各道工序，除④外，一次只能进行一道工序．小宁要将面条煮好，最少用 15 分钟．
19
已知两点A(–2,0),B(0,2), 点C是圆x2+y2–2x=0上的任意一点,则△ABC面积的最小值是 ３＋
.
20 函数f(x)满足f(nx)＝[ f(x)]n，写出一个满足上述条件的函数__f(x)＝
等_____.
21 一弹性球从100米高处自由落下，每次着地后又跳回到原来的高度的一半再落下，如此继续下去，则球所经过的路程总和为 300 米.
22 若圆锥曲线
的焦距与
无关，则它的焦点坐标是 
.
23
定义符号函数
， 则不等式：
的解集是 
.
24
若数列{an}，（
*）是等差数列，则有数列
（*）也为等差数列，类比上述性质，相应地：若数列{Cn}是等比数列，且Cn>0（*），则有dn= 
（*）也是等比数列.
25
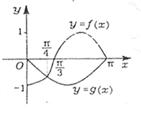
已知函数
是奇函数，它们的定域
，且它们在
上的图象如图所示，则不等式
的解集是 
.
 |
26 小明想利用树影测树高，他在某一时刻测得长为1m的竹竿影长0.9m，但当他马上测树高时, 因树靠近一幢建筑物,影子不全落在地面上,有一部分影子上了墙如图所示.他测得留在地面部分的影子长2.7m, 留在墙壁部分的影高1.2m, 求树高的高度（太阳光线可看作为平行光线）__4.2m______.
27 设正实数m,x,y,z都不等于1，实数a,b,c互不相等。给出下面三个论断：
①a,b,c成等差数列；
②x,y,z成等比数列；
③-
。
以其中两个论断作为条件，另一个论断作为结论，写出你认为正确的所有命题__①，
②
③；②，③①；③，①②____.（用序号和“”组成答案）
28 中共中央十六大提出建设有中国特色的社会主义战略目标，我国国内生产总值到2020
年比2000年要翻两番，全面建设小康社会，为实现这一目标每年的经济增长率至少应
为 7.2% .（精确到0.001，
，
，
）.
29
某工厂生产的产品第二年比第一年增长的百分率为a，第三年比第二年增长的百分率为2a－1，第四年比第三年增长的百分率为4－3a，设年平均增长率为y，且
，则y的最大值为 1
.
30
对任意的函数
在公共定义域内，规定
若
的最大值为 1
.
31 仓库有一种堆垛方式，如图（3）所示，最高一层2盒，第二层6
盒，第三层12盒，第四层20盒，……请你写在堆放层数
与盒
数n的一个关系 
.
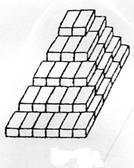
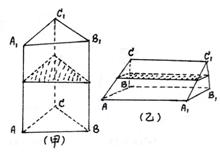
32 甲图所示是一个正三棱柱的容器，高为2
，内装水若干，将容器放倒，把一个侧面作为底面，乙图所示，这时水面恰好为中截面，则乙图中所示水面的高度是 
______.
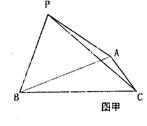
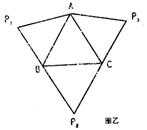
33 将三棱锥P—ABC（如图甲）沿三条侧棱剪开后，展开成如图乙的形状，其中P1，B，P2共线，P2，C，P3共线，且P1P2=P2P3，则在三棱锥P—ABC中，PA与BC所成的角是 90° .
34
对于函数
，给出下列四个命题：
①存在
；
②存在
恒成立；
③存在
，使函数
的图像关于y轴对称;
④函数
的图象关于点
对称；
其中正确命题的序号是 ①③④
35 要制造一个底面半径为4cm，母线长为6cm的圆锥，用一块长方形材料做它的侧面，这样的长方形的长与宽的最小值分别是 12cm,9cm
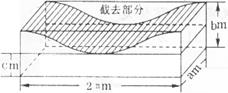
36 一块长方形木料，按图中所示的余弦线截去一块，则剩余部分的体积是__
____.
 |