数学试题
选择题集锦
陕西特级教师 安振平
1.
满足不等式
的
的最小实数值是
(A) –1 (B) 0 (C) 1 (D) 3
2.
在
中, AB=5, 
, 则<CAB的最小值为
(A) 
(B) 
(C)
(D) 
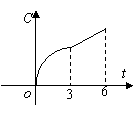
3. 某工厂六年来生产某种产品的情况是：前三年年产量的增长速度越来越快，后三年年产量保持不变，则该厂六年来这种产品的总产量C与时间t（年）的函数关系可用图像表示的是.
 |  |  |  | ||||||
 | |||||||||
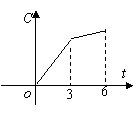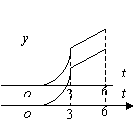( A.) ( B) ( C ) (D )
4.
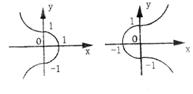
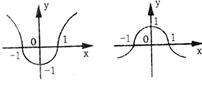
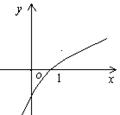
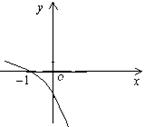
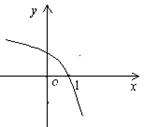
函数
的图像如图甲所示，则函数
的图像可能是( ).
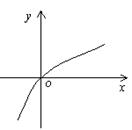
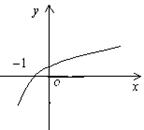
(A) (B) （甲）
（C） (D)
5.
设
，且
，则
等于
(A)
（B）
（C）
（D）
6.
已知函数
是奇函数，当
时，
，且
，则a等于
（A）
(B).
(C)
(D). 
7.
函数
，对于任意的
，都有
，则
的最小值为
(A) 
(B)
(C) 
(D)
8.
某台风在坐标平面上以等速直线行进，上午7时台风中心位于点
，上午9时位于点
，则下午5时台风中心位于点
(A)
(B) 
(C) 
(D)
9. 若一个四面体由长度为1，2，3的三种棱所构成，则这样的四面体的个数是
(A) 2 (B ) 4 (C ) 6 (D) 8
10. 汽车牌照由26个英文字母和0—9这10个数字组成。某地区若使用2个字母后接3个数字的方式构成汽车牌照，那么共有牌照
(A) 468000个 (B )650000个 (C) 486720个 (D) 676000个
11.
已知曲线C的方程为
，则曲线C的大致图象是
|
|
|
12.
函数
的自变量x从n变到n+1（n∈N）时，y恰好从－∞变到+∞，则常数a的值为
(A) 1 (B
) 2 (C) (D) 
13. 某农贸市场出售西红柿，当价格上涨时，供给量相应增加，而需求量相应减少，具体调
查结果如下表：
表1 市场供给量 表2 市场需求量
 |
根据以上提供的信息，市场供需平衡点（即供给量和需求量相等时的单价）应在区间
( A )（2.3，2.6）内 (B ) （2.4，2.6）内
(C) （2.6，2.8）内 ( D) （2.8，2.9）内
14.
函数
的图象是平面上到两定点距离之差的绝对值等于定长的点的轨迹，则这个定长为
(A) 
(B)
(C)
(D) 2
15.
C是曲线
上一点，CD
轴，D是垂足，A点坐标是（－1，0），设
（其中O表示原点），将AC+CD表示成关于
的函数
则=
（ ）
（A）
（B）
（C）
（D）
16. 据卫生部门初步统计，到2002年底，我国爱滋病病毒实际感染人数已达到100万人，且平均以每年30%的速度递增，如果不加以控制，那么，到2010年底我国爱滋病病毒实际感染人数将达到
(A ) 700万人 ( B ) 742万人
( C) 800万人 ( D ) 816万人
17. 如图，在一根长11cm，外圆周长6cm的圆柱形柱体外表面，用一根细铁丝缠绕，组成10个螺旋，如果铁丝的两端恰好落在圆柱的同一条母线上，则铁丝长度的最小值为
|
（A）61 cm （B）  cm （C） |
cm （D）
cm18. 已知
，那么
的各项系数和为
（A）8 （B）9
（C）10 （D）11
19. 用一张钢板制做一个容积为4 的无盖长方体水箱，可用的钢板有四种不同的规格（长×宽的尺寸如各选项所示，单位均为）若既要够用，又要所剩最少，则应选择钢板的规格是 （ ）
(A ) 2×5 ( B ) 2×5.5 (C ) 2×6.1 ( D ) 3×5
20.
如图，在正方体ABCD-A1B1C1D1中，E为CC1的中点，过点E作一条直线与直线A1D1和AB都相交，则这样的直线
(A) 有三条 ( B ) 有两条
(C ) 仅有一条 ( D ) 不存在
21. 某厂有一批长为2.5 m的条形钢材，要截成60 cm长的A型和43 cm长的B型的两种规格的零件毛坯，则下列哪种方案最佳（所剩材料最少）
( A ) A型4个 ( B ) A型2个，B型3个
( C ) A型1个，B型4个 ( D ) B型5个
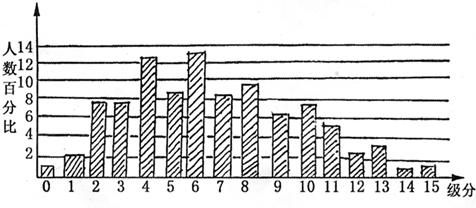
22. 九○年度大学学科能力测验有12万名学生，各学科成绩采用15级分，数学学科能力测验成绩分布图如下图。请问有多少考生的数学成绩级分高于11级分？选出最接近的数目
|
23.
不等式组 
表示的平面区域是
(A ) 矩形 ( B) 三角形 (C ) 直角梯形 (D ) 等腰梯形
24.
设A是已知复数，
是已知实数，且
， 则满足关系式：
的复数
在复平面上对应的点M的轨迹是
(A) 双曲线 ( B) 椭圆 ( C ) 圆 ( D ) 直线
25.
国际上通常用恩格尔系数来衡量一个国家和地区人民生活水平状况，它的计算公式
（x：人均食品支出总额，y：人均个人消费支出总额），且
，各种类型家庭：
| 家庭类型 | 贫困 | 温饱 | 小康 | 富裕 |
| n | n≥59% | 50%≤n＜59% | 40%≤n＜50% | 30%≤n＜40% |
李先生居住地2002年比98年食品价格下降了7.5%，该家庭在2002年购买食品和98年完全相同的情况下人均少支出75元，则该家庭2002年属于
(A ) 贫困 ( B) 温饱 ( C) 小康 (D ) 富裕
26. 设
，对所有实数x均满足xf(x)≤g(x)，那么函数g(x)可以是
（A）g(x)=sinx （B）g(x)=x
（C）
（D）g(x)=x
27. 用记号“+”表示求两个实数a与b的算术平均数的运算，即a+b=
.已知数列{xn}满足x1=0,x2=1,xn=xn-1+xn-2(n≥3),则
等于
(A ) 0
( B) 
(C ) 
(
D ) 1
28.
设
，若
，且
，则下列结论中，必成立的是
（A）
（B）
（C）
（D）
29.
关于函数f(x)＝(sinx)2－，有下面四个结论：
(1) f(x)是奇函数 ;
(2) 当x＞2003时, f(x)＞恒成立;
(3)
f(x)的最大值是 ;
(4) f(x)的最小值是－ .
其中正确结论的个数为
( A ) 1个 ( B ) 2个 (
C ) 3个
( D ) 4个
30. 台风中心从A地以每小时20千米的速度向东北方向移动，离台风中心30千米内的地区为危险区，城市B在A的正东40千米处，B城市处于危险区内的时间为
( A ) 0.5小时 ( B ) 1小时 ( C ) 1.5小时 ( D ) 2小时
31.
在直角坐标系xOy中，已知△AOB三边所在直线的方程分别为
，
则△AOB内部和边上整点（即横、纵坐标均为整数的点）的总数是
(A ) 95 ( B ) 91 ( C ) 88 ( D ) 75
32. 某商场开展促销抽奖活动，摇奖器摇出的一组中奖号码是6，5，2，9，0，4.参抽奖的每位顾客从0，1…，9这十个号码中抽出六个组成一组.如果顾客抽出的六个号码中至少有5个与摇奖器摇出的号码相同（不计顺序）就可以得奖，某位顾客可能获奖的概率为
( A ) 
(
B ) 
(
C ) 
( D ) 
33.
函数
在区间
上有最小值，则函数
在区间
上一定
(A) 有最小值 (B) 有最大值
(C) 是减函数 (D) 是增函数
34.
平行移动抛物线
，使其顶点的横坐标非负，并使其顶点到点
的距离比到y轴的距离多
，这样得到的所有抛物线所经过的区域是
（A）xOy平面
（B）
（C）
（D）
35. 某体育彩票规定：从01至36共36个号中抽出7个号为一注，每注2元.某人想从01至10中选3个连续的号，从11至20中选2个连续的号，从21至30中选1个号，从31至36中选1个号组成一注，则这人把这种特殊要求的号买全，至少要花
(A)3360元 (B ) 6720元 ( C) 4320元 ( D) 8640元
36. 在三张卡片的正反面上分别写有数字0与2，3与4，5与6，且6可以作9用，把这三张卡片拼在一起表示一个三位数，则三位数的个数为
( A ) 12 ( B ) 72 ( C) 60 ( D) 40
37. 在某学校，星期一有15名学生迟到，星期二有12名学生迟到，星期三有9名学生迟到，如果有22名学生在这三天中至少迟到一次，则三天都迟到的学生人数的最大可能值是
( A) 5 ( B) 6 (C ) 7 ( D) 8
38. 花坛水池中央有一喷泉，水管OP=1m，水从P点喷出后呈抛物线状，若最高点距水面2m，点P距离抛物线对称轴1m，则在水池直径的下列可选值中，最合算的是
 |  | ||
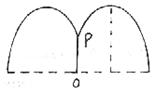( A) 2.5m (B ) 4m (C) 5m ( D) 6m
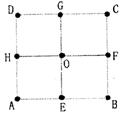
39. 如图，在正方形ABCD中，E、F、G、H是各边中点，O是正方形中心，在A，E，B，F，C，G，D，H，O这九个点中，以其中三个点为顶点作三角形，在这些三角形中，互不全等的三角形共有
(A ) 6个 ( B ) 7个 ( C ) 8个 ( D ) 9个
40.
平面直角坐标系内，一个圆心在(a, b)的圆包含原点(0, 0)，设此圆在第1象限及第3象限的面积和为
，在第2象限及第4象限的面积和为
，则
（A）
（B）
（C）
（D）（当
时），或
（当
时）