阜阳十中数学专题之函数、导数、不等式
供稿人: 李早生 2006-3-6
1. 设函数![]() 的图象与
的图象与![]() 的图象关于直线
的图象关于直线![]() 对称,
对称,
那么![]() 值等于 B
值等于 B
(A)-1 (B)-2 (C)![]() (D)
(D)![]()
2. 一元二次方程![]() 有一个正根和一个负根的充分不必要条件是:C
有一个正根和一个负根的充分不必要条件是:C
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. 已知![]() ,当
,当![]() R时,
R时,![]() 恒为正值,则
恒为正值,则![]() 的取值范围是
( B )
的取值范围是
( B )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4. 方程![]() 有一个负根且无正根,则
有一个负根且无正根,则![]() 的取值范围是
( D )
的取值范围是
( D )
![]()
![]()
![]()
![]()
![]()
![]() ≤
≤![]()
![]()
![]() ≥
≥![]()
5. ![]() ≤
≤![]() 的解集是
的解集是![]() ,则
,则![]() 的取值范围是
( A )
的取值范围是
( A )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
6. 已知映射f:A→B,其中A=B=R,对应法则为f:x→y=x2+2x+3,若对实数k∈B,在集合A中不存在原象,则k的取值范围是B
A、(-∞,0) B、(-∞,2) C、(2,+∞) D、(3,+∞)
7. 已知函数f(x)是定义在R上的奇函数,且f(x)=-f(x+2),当0≤x≤1时,![]() ,那么使
,那么使![]() 成立的x的值为D
成立的x的值为D
A、2n(n∈Z) B、2n-1(n∈Z)
C、4n+1(n∈Z) D、4n-1(n∈Z)
8. 若不等式![]() >
>![]() 在
在![]() 上有解,则
上有解,则![]() 的取值范围是( B )
的取值范围是( B )
A. ![]() B.
B. ![]()
C. ![]() D.
D.![]()
9. 已知![]() 是偶函数,则函数
是偶函数,则函数![]() 的图象的对称轴是( D )
的图象的对称轴是( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10. 已知函数![]() 满足
满足![]() 且
且![]() ∈[-1,1]时,
∈[-1,1]时,![]() ,则方程
,则方程![]()
![]() 解的个数是C:
解的个数是C:
A.4 B. 6 C.8 D. 10
11. 已知多项式16x4+32x3+24x2+8x+1能被5整除,则满足条件的最小自然数x的值为( C )
A. 7 B. 4 C. 2 D. 1
12. 一个棱锥被平行于底面的截面截成一个小棱锥和一个棱台(用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫棱台),若小棱锥的体积为y,棱台的体积为x,则y关于x的函数图象大致形状为(C )。
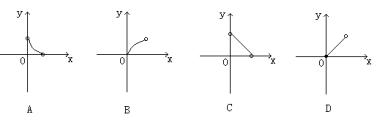
13. 已知函数f(x)定义域为R,则下列命题:
①y=f(x)为偶函数,则y=f(x+2)的图象关于y轴对称.
②y=f(x+2)为偶函数,则y=f(x)关于直线x=2对称.
③若函数f(2x+1)是偶函数,则f(2x)的图象关于直线 ![]() 对称.
对称.
④若f(x-2)=f(2-x),则y=f(x)关于直线x=2对称.
⑤y=f(x-2)和y=f(2-x)的图象关于x=2对称.
其中正确的命题序号是( C )
A、①②④ B、①③④ C、②③⑤ D、②③④
14. 已知关于x的方程![]() 没有实数解,则实数m的取值范围是 C
没有实数解,则实数m的取值范围是 C
(A)![]() (B)
(B) ![]()
(C) ![]() 或
或 ![]() (D)
(D)
![]()
15. 给定实数![]() ,定义
,定义![]() 为不大于
为不大于![]() 的最大整数,则下列结论不正确的是(A)
的最大整数,则下列结论不正确的是(A)
A.![]() B.
B.![]() C.
C.![]() 是周期函数 D.
是周期函数 D.![]() 是偶函数
是偶函数
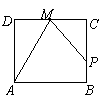
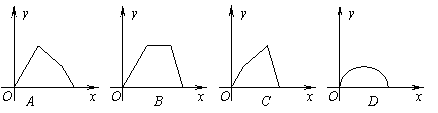
7. 如图,点P在边长为1的正方形ABCD边上运动,设点M是CD边的中点,点P沿A®B®C®M运动时,点P经过的路程记为x,△APM的面积为y,则函数y=f(x)的图象只可能是( A ).
8. 方程![]() 有五个不相等的实数根,则这五根之和为(C ).
有五个不相等的实数根,则这五根之和为(C ).
![]() 5
5 ![]() 10
10
![]() -5
-5
![]() -10
-10
9. 方程![]() 有一个负根且无正根,则
有一个负根且无正根,则![]() 的取值范围是
( D )
的取值范围是
( D )
![]()
![]()
![]()
![]()
![]()
![]() ≤
≤![]()
![]()
![]() ≥
≥![]()
10. ![]() ≤
≤![]() 的解集是
的解集是![]() ,则
,则![]() 的取值范围是
(
A )
的取值范围是
(
A )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
11. 设![]() 、
、![]() 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当![]() ,
,
且![]() ,则不等式
,则不等式![]() 的解集是 ( D
)
的解集是 ( D
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12. 设函数![]() 区间
区间![]() ,
,
则使M=N成立的实数对(a,b),有 ( A )
A.0个 B.1个 C.2个 D.无数多个
13.已知函数f1(x)=x, f2(x)=![]() ,f3(x)=4-x,函数g(x)取f1(x)、f2(x)、f3(x)中的最小值,则函数g(x)的最大值是 1
,f3(x)=4-x,函数g(x)取f1(x)、f2(x)、f3(x)中的最小值,则函数g(x)的最大值是 1
14. 已知函数![]() .给下列命题:①
.给下列命题:①![]() 必是偶函数;②当
必是偶函数;②当![]() 时,
时,![]() 的图像必关于直线x=1对称;③若
的图像必关于直线x=1对称;③若![]() ,则
,则![]() 在区间[a,+∞
在区间[a,+∞![]() 上是增函数;④
上是增函数;④![]() 有最大值
有最大值![]() .
.
其中正确的序号是__③
15. 设函数f(x)=lg(x2+ax-a-1),给出下列命题:
①f(x)有最小值;②当a=0时,f(x)的值域为R;
③当a>0时,f(x)在区间[2,![]() 上有反函数;
上有反函数;
④若f(x)在区间[2,![]() 上单调递增,则实数a的取值范围是a≥-4,
上单调递增,则实数a的取值范围是a≥-4,
则其中正确的命题是_____②③(把正确命题的序号都填上)。
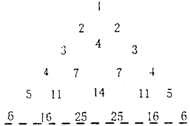 16. 如右图,它满足:(1)第n行首尾两数均为n,
16. 如右图,它满足:(1)第n行首尾两数均为n,
(2)表中的递推关系类似杨辉三角,则第n行
(n≥2)第2个数是![]()
13. 已知二次函数f(x)= x2-3x + p-1,若在区间[0,1]内至少存在一个实数c,
使f(c)>0,则实数p的取值范围是__ (1,+∞)
14. 已知函数![]() .给出下列命题:①f(x)必是偶函数;②f(0)= f(2)时,f(x)的图象必关于直线x=1对称;③若
.给出下列命题:①f(x)必是偶函数;②f(0)= f(2)时,f(x)的图象必关于直线x=1对称;③若![]() ,则f(x)在区间
,则f(x)在区间![]() 上是增函数;
上是增函数;
④f(x)有最小值![]() .
其中正确命题的序号是.③ .
.
其中正确命题的序号是.③ .
15. 若直线y=2a与函数y=ax-1(a>0,且a≠1)的图象有两个公共点,则a的取值范围是_ ![]() ______.
______.
17. 已知函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() .试求函数
.试求函数![]() (
(![]() )的最小正周期和最值
)的最小正周期和最值
解: ![]()
![]() ……2’
……2’
![]()
![]()
![]() …………………………4’
…………………………4’
当![]() >0时,
>0时,![]()
![]() ,
,![]()
解得![]() ,………………………………………………………………6’
,………………………………………………………………6’
从而,![]()
![]() ,
,
T=![]() ,最大值为5,最小值为-5;………………………………………………8’
,最大值为5,最小值为-5;………………………………………………8’
当m<0时, 解得![]() ,………………………………………………10’
,………………………………………………10’
从而,![]() ,T=
,T=![]() ,最大值为
,最大值为![]() ,
,
最小值为![]() .……………………………………………………………………12
.……………………………………………………………………12
19. 已知函数:![]() .
.
(1)证明:f(x)+2+f(2a-x)=0对定义域内的所有x都成立;
(2)当f(x)的定义域为[a+![]() ,a+1]时,求证:f(x)的值域为[-3,-2];
,a+1]时,求证:f(x)的值域为[-3,-2];
(3)设函数g(x)=x2+(x-a)f(x) ,求g(x) 的最小值
解(1)证明:![]()
![]() .
.
∴结论成立 ………………………………………………………………………………4’
(2)证明:![]()
当![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() .
.
即![]() .………………………………………………………………8’
.………………………………………………………………8’
(3)![]()
①当![]() .
.
如果![]() 即
即![]() 时,则函数在
时,则函数在![]() 上单调递增,
上单调递增,
∴![]() .
.
如果![]() .
.
当![]() 时,
时,![]() 最小值不存在.……………………………………………………10’
最小值不存在.……………………………………………………10’
②当![]() ,
,
如果![]() .
.
如果![]() .
.
当![]() .
.
![]() .……………………………………………12’
.……………………………………………12’
综合得:当![]() 时, g(x)最小值是
时, g(x)最小值是![]() ;当
;当![]() 时, g(x)最小值是
时, g(x)最小值是![]() ;当
;当![]() 时, g(x)最小值为
时, g(x)最小值为![]() ;当
;当![]() 时, g(x)最小值不存在.
时, g(x)最小值不存在.
18.在△ABC中,已知![]() .(I)若任意交换
.(I)若任意交换![]() 的位置,
的位置,![]() 的值是否会发生变化?试证明你的结论; (II)求
的值是否会发生变化?试证明你的结论; (II)求![]() 的最大值.
的最大值.
解:(I)∵ ![]()
![]()
![]()
![]()
![]()
![]() ,
,
∴ 任意交换![]() 的位置,
的位置,![]() 的值不会发生变化.
的值不会发生变化.
(II)将![]() 看作是关于
看作是关于![]() 的二次函数.
的二次函数.![]()
![]() .
.
所以,当![]() ,且
,且![]() 取到最大值1时,也即
取到最大值1时,也即![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
也可有如下简单解法:
![]()
![]()
![]()
19.已知偶函数f (x),对任意x1,x2∈R,恒有:![]() .
.
(1)求f (0),f (1),f (2)的值;
(2)求f (x);
(3)判断![]() 在(0,+∞)上的单调性
在(0,+∞)上的单调性
解:(1) f (0) = -1,f (1) = 0,f (2) = 3;
(2)![]() ,
,
又![]() ,f (0) = -1,故
,f (0) = -1,故![]() ;
;
(3)![]() .用定义可证明
.用定义可证明![]() 在[,+∞)上是增函数,
在[,+∞)上是增函数,
在(0,]上为减函数
20.已知函数f(x)=x4-4x3+ax2-1在区间[0,1)上单调递增,在区间[1,2)上单调递减.
(Ⅰ)求a的值;
(Ⅱ)若点A(x0,f(x0))在函数f(x)的图象上,求证点A关于直线x=1的对称点B也在函数f(x)的图象上;
(Ⅲ)是否存在实数b,使得函数g(x)=bx2-1的图象与函数f(x)的图象恰有3个交点.若存在,请求出实数b的值;若不存在,试说明理由.
解:(Ⅰ)由函数f(x)=x4-4x3+ax2-1,在区间[0,1)上单调递增,在区间[1,2)上单调递减,
∴x=1时,f(x)取得极大值,∴f′(1)=0. 2分
f′(x)=4x3-12x2+2ax, ∴4-12+2a=0![]() a=4. 4分
a=4. 4分
(Ⅱ)点A(x0,f(x0))关于x=1的对称点B坐标为(2-x0,f(x0)), 6分
f(2-x0)=(2-x0)4-4(2-x0)3+4(2-x0)2-1=(2-x0)2[(2-x0)-2]2-1
=x04-4x03+4x02-1=f(x0). 8分
∴点A关于直线x=1的对称点B也在函数f(x)的图象上. 9分
(Ⅲ)函数g(x)=bx2-1的图象与函数f(x)的图象恰有3个交点,等价于方程x4-4x3+4x2-1=bx2-1恰有3个不等实根, 10分
x4-4x3+4x2-1=bx2-1![]() x4-4x3+(4-b)x2=0.
x4-4x3+(4-b)x2=0.
∵x=0是其中一个根,
∴方程x2-4x+(4-b)=0有两个非0不等实根. 12分
∴![]() ∴b>0且b≠4. 14分
∴b>0且b≠4. 14分
22.已知函数f(x)=-x3+ax2+b(a,b∈R)
(1)若函数y=f(x)图像上任意不同的两点连线斜率小于1,求证:-![]() <a<
<a<![]()
若x∈[0,1],函数y=f(x)上任一点切线斜率为k,讨论|k|≤1的充要条件
解:(1)设任意不同的两点P1(x1,y1),P2(x2,y2),且x1≠x2
则![]() <1
(1分)
<1
(1分)
∴![]() <1
<1
即-x12-x1x2-x22+a(x1+x2)<1
∴-x12+(a-x2)x1-x22+ax2-1<0 (3分)
∵x1∈R
∴Δ=(a-x2)2+4(-x22+ax2-1)<0
即-3x22+2ax2+a2-4<0
∴-3(x2-![]() )2+
)2+![]() +a2-4<0
+a2-4<0
∴![]() a2-4<0,∴-
a2-4<0,∴-![]() <a<
<a<![]() (6分)
(6分)
(2)当x∈[0,1]时,k=f′(x)=-3x2+2ax(7分)
由题意知:-1≤-3x2+2ax≤1,x∈[0,1]
即对于任意x∈[0,1],|f′(x)|≤1等价于|f′(0)|,|f′(1)|,
|f′(![]() )|的值满足
)|的值满足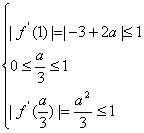
或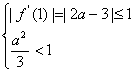 或
或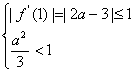 (11分)
(11分)
即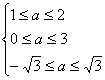 或
或 ![]() 或
或 ![]()
∴1≤a≤![]()
即|k|≤1的充要条件是1≤a≤![]()
17. 已知函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() .试求函数
.试求函数![]() (
(![]() )的最小正周期和最值
)的最小正周期和最值
解: ![]()
![]() ……2’
……2’
![]()
![]()
![]() …………………………4’
…………………………4’
当![]() >0时,
>0时,![]()
![]() ,
,![]()
解得![]() ,………………………………………………………………6’
,………………………………………………………………6’
从而,![]()
![]() ,
,
T=![]() ,最大值为5,最小值为-5;………………………………………………8’
,最大值为5,最小值为-5;………………………………………………8’
当m<0时, 解得![]() ,………………………………………………10’
,………………………………………………10’
从而,![]() ,T=
,T=![]() ,最大值为
,最大值为![]() ,
,
最小值为![]() .……………………………………………………………………12
.……………………………………………………………………12
19. 已知函数:![]() .
.
(1)证明:f(x)+2+f(2a-x)=0对定义域内的所有x都成立;
(2)当f(x)的定义域为[a+![]() ,a+1]时,求证:f(x)的值域为[-3,-2];
,a+1]时,求证:f(x)的值域为[-3,-2];
(3)设函数g(x)=x2+(x-a)f(x) ,求g(x) 的最小值 .
解(1)证明:![]()
![]() .
.
∴结论成立 ………………………………………………………………………………4’
(2)证明:![]()
当![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() .
.
即![]() .………………………………………………………………8’
.………………………………………………………………8’
(3)![]()
①当![]() .
.
如果![]() 即
即![]() 时,则函数在
时,则函数在![]() 上单调递增,
上单调递增,
∴![]() .
.
如果![]() .
.
当![]() 时,
时,![]() 最小值不存在.……………………………………………………10’
最小值不存在.……………………………………………………10’
②当![]() ,
,
如果![]() .
.
如果![]() .
.
当![]() .
.
![]() .……………………………………………12’
.……………………………………………12’
综合得:当![]() 时, g(x)最小值是
时, g(x)最小值是![]() ;当
;当![]() 时, g(x)最小值是
时, g(x)最小值是![]() ;当
;当![]() 时, g(x)最小值为
时, g(x)最小值为![]() ;当
;当![]() 时, g(x)最小值不存在.
时, g(x)最小值不存在.
20. 已知集合![]() ,试问集合A与B共有几个相同的元素,并写出由这些“相同元素”组成的集合.
,试问集合A与B共有几个相同的元素,并写出由这些“相同元素”组成的集合.
解:因为![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以A、B有两个公共元素,由这些“相同元素”组成的集合是{1,9}.
21. 设关于x的一元二次方程2x2-ax-2=0的两根的α、β(α<β),函数f(x)=![]()
⑴求f(α)·f(β)的值;⑵证明f(x)是[α,β]的增函数;
(3)当a为何值时,f(x)在区间[α,β]上的最大值与最小值之差最小?
解:⑴ f(α)f(β)=-4
⑵设α≤x1<x2≤β,f(x1)-f(x2)=![]() 17. 已知函数
17. 已知函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() .试求函数
.试求函数![]() (
(![]() )的最小正周期和最值
)的最小正周期和最值
解: ![]()
![]() ……2’
……2’
![]()
![]()
![]() …………………………4’
…………………………4’
当![]() >0时,
>0时,![]()
![]() ,
,![]()
解得![]() ,………………………………………………………………6’
,………………………………………………………………6’
从而,![]()
![]() ,
,
T=![]() ,最大值为5,最小值为-5;………………………………………………8’
,最大值为5,最小值为-5;………………………………………………8’
当m<0时, 解得![]() ,………………………………………………10’
,………………………………………………10’
从而,![]() ,T=
,T=![]() ,最大值为
,最大值为![]() ,
,
最小值为![]() .……………………………………………………………………12
.……………………………………………………………………12