综合测试卷(二)理科
一、 选择题:(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
![]()
![]() 1、已知集合
,
,U=N,那么A∩(CUB)=(
)
1、已知集合
,
,U=N,那么A∩(CUB)=(
)
A . {1,2,3,4,5} B . {2,3,4,5}
C . {3,4,5} D . {x1<x≤5}
2、已知a>b,则不等式① <,② >,③ a2>b2,④ ac>bc(c≠0)中不能恒成立的是 ( )
A. 1个 B. 2个 C. 3个 D. 4个
3、下列各组函数中,表示同一函数的是 ( )
A.![]() B.
B. ![]()
C.![]() D.
D. ![]()
4.设甲、乙两名射手各打了10发子弹,每发子弹击中环数如下:
甲:10,6,7,10,8,9,9,10,5,10;
乙:8,7,9,10,9,8,7,9,8,9
则甲、乙两名射手的射击技术评定情况是: ( )
A.甲比乙好 B。乙比甲好 C。甲、乙一样好 D。难以确定
5.下列函数中,最小值为4的函数是 ( )
![]()
![]()
![]()
![]()
A. B. C. D.
6.已知-9,a1,a2,-1四个实数成等差数列, -9,b1,b2,b3,-1五个实数成等比数列,则
b2(a2-a1)= ( )
A. 8 B. -8 C. ±8 D.
7.圆锥的轴截面是等腰直角三角形,且圆锥的底面积为10,则它的侧面积为 ( )
![]()
![]() A .10 B. 10 C.
5 D.
5
A .10 B. 10 C.
5 D.
5
8、已知实数![]() 满足
满足![]()
![]() ≥
≥![]() ,则
,则![]() 的取值范围是 ( )
的取值范围是 ( )
(A)![]() ≤
≤![]() 或
或![]() ≥
≥![]() (B)
(B)![]() ≤
≤![]() ≤
≤![]()
(C)![]() ≤
≤![]() 或
或![]() ≥
≥![]() (D)
(D)![]() ≤
≤![]() ≤
≤![]()
二.填空题:(本大题共4小题;每小题5分,共20分.)
9.已知复数z满足(![]() +3i)z=3i,则z= 。
+3i)z=3i,则z= 。
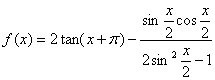 10、在面积为S的ΔABC内任取一点P,则ΔPAB的面积大于 的概率为
.
10、在面积为S的ΔABC内任取一点P,则ΔPAB的面积大于 的概率为
.
11.已知 ,则 .
 |
12.已知x,y满足不等式组 ,则S=6x+8y的最大值是 .
 |
13.运行右边框内的程序,在两次
运行中分别输入 -4 和 4,则运行
结果依次为 .
14.电视台连续播放6个广告,其中含4个不同的商业广告和2个不同的公益广告,要求首尾必须播放公益广告,则共有 种不同的播放方式
![]()
![]() 三.解答题:(本大题共6小题,共80分.解答应写出文字说明、证明过程或推证过程.)
三.解答题:(本大题共6小题,共80分.解答应写出文字说明、证明过程或推证过程.)
15.(本题满分12分) 已知α为锐角,向量 ,且
![]()
![]() (1)求 的值.
(1)求 的值.
![]() (2)若
,求向量 的夹角的余弦值.
(2)若
,求向量 的夹角的余弦值.
16. (本题满分12分) 下表为某班英语及数学成绩的分布.学生共有50人,成绩分为5个档次,如表中所示
英语成绩为5分、数学成绩为4分的学生有3人。若在全班学生中任选一人,其英语
|
| 数 学 | |||||
| 5 | 4 | 3 | 2 | 1 | ||
| 英 语 | 5 | 1 | 3 | 1 | 0 | 1 |
| 4 | 1 | 0 | 7 | 5 | 1 | |
| 3 | 2 | 1 | 0 | 9 | 3 | |
| 2 | 1 | b | 6 | 0 | a | |
| 1 | 0 | 0 | 1 | 1 | 3 | |
语成绩记为![]() ,数学成绩记为
,数学成绩记为![]() .
.
(1) ![]() 的概率是多少?
的概率是多少?![]() 且
且![]() 的
的
概率是多少?
(2) 若![]() 的期望为
的期望为![]() ,试确定a,b的值.
,试确定a,b的值.
17、(本题满分14分) 在棱长为2的斜三棱柱![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,连结
,连结![]() .
.
(Ⅰ)求证:![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.;
的大小.;
 (Ⅲ)求三棱锥
(Ⅲ)求三棱锥![]() 的体积.
的体积.
18.(本小题满分14分)设![]() 为等差数列,
为等差数列,![]() 为数列
为数列![]() 的前
的前![]() 项和,已知
项和,已知![]() ,
,![]() .
.
(1) 求数列![]() 的通项公式;
的通项公式;
(2) ![]() 若 ,求数列
若 ,求数列![]() 的前
的前![]() 项和
项和![]() 。
。
19. (本小题满分14分)
已知函数![]() 的图象为曲线E.
的图象为曲线E.
(1) 若曲线E上存在点P,使曲线E在P点处的切线与x轴平行,求a,b的关系;
(2) 说明函数![]() 可以在
可以在![]() 和
和![]() 时取得极值,并求此时a,b的值;
时取得极值,并求此时a,b的值;
(3) 在满足(2)的条件下,![]() 在
在![]() 恒成立,求c的取值范围.
恒成立,求c的取值范围.
20. (本题满分14分)
已知椭圆![]()
![]() 过点
过点![]() ,且与
,且与![]() 的交于
的交于![]() ,
,![]() .
.
(1)
用![]() 表示
表示![]() ,
,![]() 的横坐标;
的横坐标;
(2)
设以![]() 为焦点,过点
为焦点,过点![]() ,
,![]() 且开口向左的抛物线的顶点坐标为
且开口向左的抛物线的顶点坐标为![]() ,求实数
,求实数![]()
的取值范围.
综合测试卷(二)理科
一、选择题:(每小题5分,共40分)
1.B 2.D 3.D 4.B
5.C 6.B 7.A 8.A
二填空题:(每小题5分,共30分)
9.![]()
10.
11. -
12. 24
13. -1,20
14.48
三、解答题(6小题,共80分)
15. ![]() 解:(1)
解:(1)
![]() ∵
∵
![]() ∴
……………………………………………… 2分
∴
……………………………………………… 2分
∴
![]()
![]() 即
…………………………………………… 4分
即
…………………………………………… 4分
又因为α为锐角,所以 ……………………………… 6分
![]()
![]() (2)解法一:
(2)解法一:
由 得
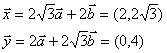 ∴
∴
…………………………………………… 9分
![]() 设向量
的夹角为θ
设向量
的夹角为θ
![]() 则
则
……………………………… 12分
![]() 解法二:
解法二:
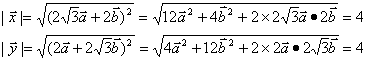 由已知可得
………………………………… 7分
由已知可得
………………………………… 7分
所以
…………………………………………… 10分
![]() 设向量 的夹角为θ
设向量 的夹角为θ
![]()
则 ……………………………… 12分
16.解:显然![]() 是随机变量.
是随机变量.
(1)![]() .
.![]() . …………………………………6分
. …………………………………6分
(2)由![]() 的期望为
的期望为![]() ,得
,得
![]() ,即
,即![]() . …………………9分
. …………………9分
根据表中数据,得![]() ,即
,即![]() . ………………………………………………11分
. ………………………………………………11分
联立解得![]() . …………………………………………………………………………………………12分
. …………………………………………………………………………………………12分
17、(Ⅰ)![]() 证明:∵
证明:∵![]() 是菱形,
是菱形,
 ∴
∴ ![]() ⊥
⊥![]() ……………………..1分
……………………..1分
又∵ ![]() ⊥
⊥![]() ,且
,且![]()
∴![]() ⊥平面
⊥平面![]() , ……………………..3分
, ……………………..3分
而AO![]() 平面
平面![]()
∴![]() ⊥
⊥![]()
∵![]() ,
,![]() ∴
∴![]()
∴![]() ⊥
⊥![]() ,且
,且![]()
∴![]() ⊥平面
⊥平面![]() . ……………5分
. ……………5分
(Ⅱ) 取![]() 的中点
的中点![]() ,连结
,连结![]() 、
、![]()
![]() ∵
∵![]() 是等边三角形 ∴
是等边三角形 ∴![]() ⊥
⊥![]()
∵![]() ⊥平面
⊥平面![]() ∴
∴![]() 是
是![]() 在平面
在平面![]() 上的射影,∴由三垂线定理逆定理 可得
上的射影,∴由三垂线定理逆定理 可得![]()
∴![]() 是二面角
是二面角![]() 的平面角 ……………7分
的平面角 ……………7分
![]() ≌Rt
≌Rt![]() ,则
,则![]() ,∴四边形
,∴四边形![]() 为正方形。
为正方形。
在直角三角形![]() 中,
中,![]() ,
,![]() ∴
∴![]() =
=![]() =
=![]() ………9分
………9分
∴![]() =arcsin
=arcsin![]() .(或
.(或![]() ,
,![]() )
)
∴二面角![]() 的大小是arcsin
的大小是arcsin![]() …………………………………10分
…………………………………10分
(Ⅱ) 另解:由(Ⅰ)易证
另解:由(Ⅰ)易证![]() ≌Rt
≌Rt![]() ,则
,则![]() ,
,
∴四边形![]() 为正方形。以
为正方形。以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,
FB所在直线为![]() 轴, OA所在直线为
轴, OA所在直线为![]() 轴,建立空间直角坐标系(如图),则A(0,0,
轴,建立空间直角坐标系(如图),则A(0,0,![]() ), B(0,
), B(0, ![]() ,0),C(-
,0),C(-![]() ,0,0),
,0,0),![]() =(0,
=(0,![]() ,-
,-![]() ),
),![]() =(-
=(-![]() ,0,-
,0,-![]() )
)
…………………………………………………………………….7分
设![]() =(
=(![]() )为平面
)为平面![]() 的法向量,则
的法向量,则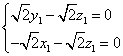
∴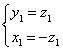 ,取
,取![]() =(-1,1,1)为平面
=(-1,1,1)为平面![]() 的一个法向量。……………8分
的一个法向量。……………8分
而![]() =(0,
=(0, ![]() ,0)为平面
,0)为平面![]() 的一个法向量。设
的一个法向量。设![]() 为
为![]() 与
与![]() 的夹角,则
的夹角,则 =
=![]() =
=![]() ………………………………………………………….9分
………………………………………………………….9分
∴二面角![]() 的大小为
的大小为![]() ……………………………………….10分
……………………………………….10分
(Ⅲ)![]() ∥
∥![]() ,
,![]()
![]()
![]() ∥平面
∥平面![]()
∴点![]() 、
、![]() 到面
到面![]() 的距离相等………………………………………………………11分
的距离相等………………………………………………………11分
![]() …………………………………………………………………..12分
…………………………………………………………………..12分
![]() …………………………………………………………14分
…………………………………………………………14分
18、(本题满分14分)
解:(1)设等差数列![]() 的公差为
的公差为![]() ,则
,则![]() …………… 2分
…………… 2分
∵
![]() ,
,![]() ,
,
∴ ![]() 即
即
![]() ……………
4分
……………
4分
解得
![]() ,
,![]() 。……………………………………………… 6分
。……………………………………………… 6分
∴ 数列![]() 的通项公式为
的通项公式为![]() …………………… 7分
…………………… 7分
(2) ![]() ………………………… 9分
………………………… 9分
∴ ![]()
![]()
![]()
………………………… 14分
19.解:(1)根据题意,![]() 有解,
有解,
∴![]() 即
即![]() . ……………………………………………………………………………3分
. ……………………………………………………………………………3分
(2)若函数![]() 可以在
可以在![]() 和
和![]() 时取得极值,
时取得极值,
则![]() 有两个解
有两个解![]() 和
和![]() ,且满足
,且满足![]() .
.
易得![]() . ………………………………………………………………………………………………6分
. ………………………………………………………………………………………………6分
(3)由(2),得![]() . ………………………………………………………………7分
. ………………………………………………………………7分
根据题意,![]() (
(![]() )恒成立. ……………………………………………9分
)恒成立. ……………………………………………9分
∵函数![]() (
(![]() )在
)在![]() 时有极大值
时有极大值![]() (用求导的方法),
(用求导的方法),
且在端点![]() 处的值为
处的值为![]() .
.
∴函数![]() (
(![]() )的最大值为
)的最大值为![]() . …………………………13分
. …………………………13分
所以![]() . …………………………………………………………………………………………………………14分
. …………………………………………………………………………………………………………14分
20.解:(1)由于椭圆![]() 过点
过点![]() ,
,
故![]() . ………………………………………………………………………………………………………………1分
. ………………………………………………………………………………………………………………1分
![]() ,
,![]() 横坐标适合方程
横坐标适合方程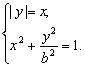
解得![]() (
(![]() 即
即![]() ).………………………………………………………4分
).………………………………………………………4分
即![]() ,
,![]() 横坐标是
横坐标是![]() (
(![]() 即
即![]() ).……………………………………5分
).……………………………………5分
(2)根据题意,可设抛物线方程为![]() . …………………6分
. …………………6分
∵![]() ,∴
,∴![]() .………………………………………………………………7分
.………………………………………………………………7分
把![]() 和
和![]() (等同于
(等同于![]() ,
,![]() 坐标(
坐标(![]() ,
,![]() ))代入式抛物线方
))代入式抛物线方
程,得![]() . ……………………………………9分
. ……………………………………9分
令![]() .……………………………………10分
.……………………………………10分
则![]() 内有根(并且是单调递增函数),
内有根(并且是单调递增函数),
∴ ………………………………………………………………13分
………………………………………………………………13分
解得![]() . …………………………………………………………………………………………14分
. …………………………………………………………………………………………14分