高三数学综合测试题(38)
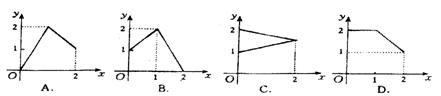
1.设集合![]() ,下列图中能表示从集合A到集合B的映
,下列图中能表示从集合A到集合B的映
射的是 ( D )
|
2.设p、q为简单命题,则“p且q为假”是“p或q为假”的 (B )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.已知函数![]() 的反函数为
的反函数为![]() ,则
,则![]() 的值为 ( A )
的值为 ( A )
A.-1 B.0 C.1 D.4
4.已知点A(2,1),B(0,2),C(-2,1),O(0,0). 给出下面四个结论:
①直线OC与直线BA平行;②![]() ;③
;③![]() ;
;
④![]() ,其中正确结论的个数是 ( C )
,其中正确结论的个数是 ( C )
A.1个 B.2个 C.3个 D.4个
5.设![]() ,则 (A )
,则 (A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.定义在R上的函数![]() 既是偶函数又是周期函数,若
既是偶函数又是周期函数,若![]() 的最小正周期是
的最小正周期是![]() ,且当
,且当
![]() ,
,![]() ,则
,则![]() 的值为 ( D )
的值为 ( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.若关于![]() 的不等式
的不等式![]() 的实数解,则实数
的实数解,则实数![]() 的取值范围是YCY ( D )
的取值范围是YCY ( D )
A.(-3,3) B.(-∞,-3) C.(-3,3![]() D.(-∞,3)
D.(-∞,3)
8.已知两直线![]() 和
和![]() ,设
,设![]() 与
与![]() 轴相交于A点,与
轴相交于A点,与![]() 相交于B
相交于B
点,![]() 与y轴相交于C点,O为原点,若O、A、B、C四点共圆,则直线
与y轴相交于C点,O为原点,若O、A、B、C四点共圆,则直线![]() 的斜率为(A Y)
的斜率为(A Y)
A.3 B.-3 C.![]() D.-
D.-![]()
9.若对任意![]() ,不等式
,不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() ( B
)
( B
)
|
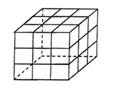
每条对角线上的数字的和相等,这个正方形就叫做n阶幻方,记
![]() 为n阶幻方对角线上数字之和,如:如图就是一个3阶幻方,
为n阶幻方对角线上数字之和,如:如图就是一个3阶幻方,
可知![]() =15,那么
=15,那么![]() =( C
)
=( C
)
A.32 B.33 C.34 D.35
11.若点P分有向线段![]() 的比为
的比为![]() ,则点P1分有向线段
,则点P1分有向线段![]() 所成的比为 1 .
所成的比为 1 .
12.曲线![]() 在点(1,-1)处的切线方程为
在点(1,-1)处的切线方程为
![]() .
.
13.已知函数![]() ,对于任意的实数
,对于任意的实数![]() 、
、![]() ,均有
,均有![]()
且![]() ,则
,则![]() =
=
1 .
14.已知函数![]() 的前n项和
的前n项和![]() ,则
,则![]() = 68;
.
= 68;
.
15.在函数![]() 中,若a、b、c成等比数列,且
中,若a、b、c成等比数列,且![]() ,则
,则![]() 有最
有最
大, 值(填“大”或“小”),且该值等于 -3. .
16. 已知A、B、C三点的坐标分别为A(3,0)、B(0,3)、C(![]() ),且
),且![]()
(1)求![]() 的值;
的值;
(2)若函数![]() 的图像按向量
的图像按向量![]() 平移后对应的函数为偶函数,
平移后对应的函数为偶函数,
且![]() 为最小,求实数m的值.
为最小,求实数m的值.
解(1)![]() ,
,
![]() ……6分
……6分
(2)易知按向量![]() 平移后,函数的解析式为
平移后,函数的解析式为![]() ,
,
由![]() 为偶函数,
为偶函数,![]()
![]() 故有
故有![]() ……………
……………
17. 已知函数![]() ,其中a为实常数.
,其中a为实常数.
(1)若![]() ,求
,求![]() 在区间[-2,2]上的最大值和最小值;
在区间[-2,2]上的最大值和最小值;
(2)若![]() 上单调递增,求a的取值范围.
上单调递增,求a的取值范围.
解:(1)![]() ,
,![]()
令![]()
此时![]()
即得![]() …………………………3分
…………………………3分
比较![]() 、
、![]() 、
、![]() 、
、![]() 得
得![]() 在[-2,2]上的最大值和最小值为
在[-2,2]上的最大值和最小值为
![]() ………………6分
………………6分
(2)![]() 恒成立,且不恒为0
恒成立,且不恒为0
令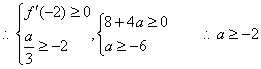 ,
,![]() 的取值范围是
的取值范围是![]() …
…
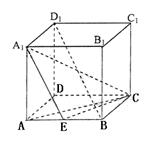
18.
|
棱三等分,然后从每个等分点把正方体锯开,得到27个棱长为1的小正
方体,将这些小正方体充分混合后,装入一个口袋中.
(1)从这个口袋中任意取出1个小正方体,这个小正方体的表面恰
好没有颜色的概率为多少?
(2)从这个口袋中同时任意取出2个小正方体,其中一个小正方体
恰好有1个面涂有颜色,另一个小正方体至少有2个面涂有颜
色的概率为多少?
解:在27个小正方体中,恰好有三个面都涂有颜色的共有8个,恰好有两个面都涂有颜色的共有12个,恰好有一个面都涂有颜色的共有6个,表面没涂颜色的1个……4分
(1)记“从这个口袋中任意取1个小正方体,这个小正方体的表面恰好没有颜色”为
事件A,则P(A)=![]() …………………………8分
…………………………8分
(2)从27个小正方体中同时任意取2个小正方体,共有![]() 种等可能的结果。这些结果
种等可能的结果。这些结果
中,有一个小正方体恰好有1个面涂颜色,另一个小正方体至少有2个面涂有颜色有
![]() 种。所以从27个小正方体中同时任意取出2个小正方体,有一个小正方
种。所以从27个小正方体中同时任意取出2个小正方体,有一个小正方
体恰好有1个面涂有颜色,另一个小正方体至少有2个面涂有颜色概率为
|
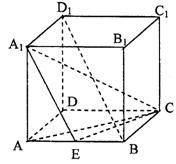
19. 如图,在正方体ABCD—A1B1C1D1中,E 为AB的中点.
(1)求异面直线BD1与A1E所成角的余弦值;
(2)求二面角A1—EC—A的大小.
解:(1)设正方体的棱长为1,延长DC至G,使![]() ,连结BG、D1G.
,连结BG、D1G.
|
|
∴BG∥EC. ∴∠D1BG就是异面直线BD1与
CE所成的角.………………2分
在△D1BG中D1B=![]() ,
,
![]()
∴cos∠D1BG=
即异面直线BD1与CE所成角的余弦值是![]() ……………………7分
……………………7分
(2)过A1作A1H⊥CE交CE的延长线于H. 连结AH. ∵AA1⊥平面ABCD,
∴AH是A1H在平面ABCD内的射影. ∴AB⊥CH.
则∠A1HA为二面角A1—EC—D的平面角.………………9分
底面ABCD如 图所示.
由于∠AHE=∠B=90°,∠AEH=∠CEB,则△AHE∽△CBE.
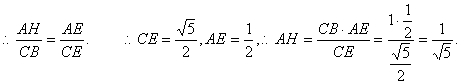 ……12分
……12分
在Rt△A1AH中,A1A=1,AH=![]() .
. ![]()
则二面角A1—EC—D的大小为arctg![]() ……………………14分
……………………14分
注:其他方法参照此标准给分
20. 已知函数![]() ,点
,点![]() 在函数
在函数![]() 图像上,且
图像上,且![]() ,
,
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前n项和为Sn,求证:
的前n项和为Sn,求证:![]()
(1)
由已知:![]() 是公差为1、首项为
是公差为1、首项为![]() 的等差数列.……(2分)
的等差数列.……(2分)
![]() ,………………………………(3分)
,………………………………(3分)
![]() ,……………………………………(4分)
,……………………………………(4分)
![]() …………(7分)
…………(7分)
(2)![]() ,………………(10分)
,………………(10分)
![]()
……………………………(12分)
![]() …………………………………………………(14分)
…………………………………………………(14分)