数学综合卷
班级______ 姓名_______ 学号_______
第Ⅰ卷（选择题 共50分）
一、选择题（本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有
一项是符合题目要求的）
1．（文）函数
的定义域是 （ ）
A．
B．
C．
D．（－1，0）
（理）复数
所对应的点在 （ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
2. 若集合
，则
（ ）
A. 
B.
C.
D.
3．已知等差数列
的通项公式为
，则
的展开式中含
项的系数是该数列的 （ ）
A．第9项 B．第10项 C．第19项 D．第20项
4. 函数
的单调减区间是（ ）
A.（
，1） B.（1，2）
C.（
，） D.（，）与（1，
）
5．设
，则下列各式中正确的是 （ ）
A．
B．
C．
D．
6．O为平面上的定点，A、B、C是平面上不共线的三点，若( 
-
)·(+-2
)=0，则DABC是（ ）
A．以AB为底边的等腰三角形 B．以BC为底边的等腰三角形
C．以AB为斜边的直角三角形 D．以BC为斜边的直角三角形
7．从4名教师与5名学生中任选3人，其中至少要有教师与学生各1人，则不同的选法共有 （）
A．140种 B．80种 C．70种 D．35种
8．甲、乙两人独立解答某道题，解不出来的概率分别为a和b，那么甲、乙两人都解出这道题的概率是 ( )
A．1-ab B．(1-a)(1-b) C．1-(1-a)(1-b) D．a(1-b)+b(1-a)
9. 如果
与
的图象关于直线
对称，则
的值为( )
A. 
B.
C.
D.
10. 设
是椭圆的两个焦点，以
为圆心，且过椭圆中心的圆与椭圆的一个交点为M，若直线
与圆相切，则椭圆的离心率是
A. 
B.
C.
D.
第Ⅱ卷（非选择题 共100分）
二、填空题（本大题共4小题，每小题4分，共16分. 把答案填在题中的横线上）
11．把函数
的图象向右平移
个单位，再把所得图象上各点的横坐标缩短
为原来的
（纵坐标不变），则所得图象的解析式为
12. 若奇函数
在
时，
，那么
时，x的集合是_____________
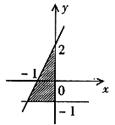
13. 表示图中阴影部分的二元一次不等式组为___________________
14. 在各项均为正数的等比数列
中，设
，则
_____________，
的值等于_____________
三、解答题（本大题共6小题，每小题14分，共84分，解答应写出文字说明，证明过程或演算步骤）
15．已知
，解关于
的不等式
16．（文）一袋中装有大小相同的3个白和4个黑球，
（1）从中摸出两个球，求两个球恰好颜色不同的概率；
（2）从中摸出一个球，放回后再摸出一个球，求两个球恰好颜色不同的概率
（理）一袋中装有6个球，编号为1、2、3、4、5、6,在袋中同时取3只球，以
表示取出的3只球中的最大号码，
（1）求的分布列； （2）求的数学期望； （3）求“
”的概率
17．设
,问：是否存在a，b，c使得等式
对一切实数x都成立？若存在，求出a，b，c的值；若不存在，请说明理由
18．已知函数
处取得极值.
（Ⅰ）求函数
的解析式；
（Ⅱ）求函数的单调区间
19. 已知椭圆
的离心率是
，F是其左焦点，若直线
与椭圆交于AB两点，且
，求该椭圆的方程
20．已知数列
的前
项和
．
(Ⅰ) 判断数列是否为等差数列；
(Ⅱ) 设
，求
；
(Ⅲ) 设
，是否存在最大的自然数
，使得不等式
对一切自然数总成立？如果存在，求出
的值；如果不存在，说明理由