数学综合练习二
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设M={yy=3-x2,x∈R},N={yy=2x2-1,x∈R},则M![]() N=
N=
A.{y-3![]() y
y![]() 13} B.{y-1
13} B.{y-1![]() y
y![]() 3} C.{
3} C.{![]() }
D.{
}
D.{![]() -
-![]() }
}
2.函数![]() 在
在![]() 上的最大值是
上的最大值是
A.2 B.1 C.![]() D.0
D.0
3.已知直线l:![]() ,则直线1的倾斜角为
,则直线1的倾斜角为
A.![]() B.-
B.-![]() C.
C.![]() D.
D.![]()
4.有10级台阶,一次每步跨上一级,二级或三级,共7步走完,则不同的走法总数是
A.175 B.42 C.77 D.35
5.已知i, j为互相垂直的单位向量,a = i – 2j,
b = i + λj,且a与b的夹角为锐角,则实数![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.将函数f(x)=tan(2x+![]() )+1按向量a 平移得到奇函数g(x),要使a最小,则a=
)+1按向量a 平移得到奇函数g(x),要使a最小,则a=
A.(![]() ) B.(
) B.(![]() )
C.(
)
C.(![]() )
D.(
)
D.(![]() )
)
7.![]() ,则方程
,则方程![]() 在(0,2)上恰好有
在(0,2)上恰好有
A. 0 个根 B. 1个根 C.2个根 D. 3个根
8.![]() 是定义在R上的奇函数,它的最小正周期为T,则
是定义在R上的奇函数,它的最小正周期为T,则![]() 的值为
的值为
A.0
B.![]() C.T
D.
C.T
D.![]()
9.在直角坐标系中,O是原点,![]() =(-2+cosθ,-2+sinθ) (θ∈R),动点P在直线x=3上运动,若从动点P向Q点的轨迹引切线,则所引切线长的最小值为
=(-2+cosθ,-2+sinθ) (θ∈R),动点P在直线x=3上运动,若从动点P向Q点的轨迹引切线,则所引切线长的最小值为
A.4 B.5 C.2![]() D.
D.![]()
10.已知P为抛物线y=2x2+1上的动点,定点A(0,-1).点M分![]() 所成的比为2,则点M的轨迹方程为
所成的比为2,则点M的轨迹方程为
A.y=6x2-![]() B.x=6y2-
B.x=6y2-![]() C.y=3x2+
C.y=3x2+![]() D.y=-3x2-1
D.y=-3x2-1
11.教师想从52个学生中抽取10名分析期中考试情况,一小孩在旁边随手拿了两个签,教师没在意,在余下的50个签中抽了10名学生.则其中的李明被小孩拿去和被教师抽到的概率分别为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.某工厂投入98万元购买一套设备,第一年的维修费用12万元,以后每年增加4万元,每年可收入50万元.就此问题给出以下命题:①前两年没能收回成本;②前5年的平均年利润最多;③前10年总利润最多;④第11年是亏损的;⑤10年后每年虽有盈利但与前10年比年利润有所减少.(总利润=总收入-投入资金-总维修费)其中真命题是
A.①②⑤ B.①③⑤ C.①③④ D.②③④
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题4个小题,每小题4分,共16分.
13.已知有公共端点的向量a、b不共线,a=1,b=2.则与向量a、b的夹角平分线平行的单位向量是______________.
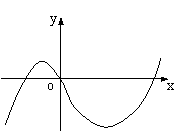 14.函数f(x)=ax3+bx2+cx+d的图象(如图),则实数a、b、c、d与零的
14.函数f(x)=ax3+bx2+cx+d的图象(如图),则实数a、b、c、d与零的
大小关系是__________;方程f(x)=f’(x)实根的个数_____________.
15.设命题p: (x.y∈R),命题q:x2+y2
(x.y∈R),命题q:x2+y2![]() r2(x、
r2(x、
y、r∈R,r>0),若命题q是命题¬p的充分非必要条件,则r的最大值为__________.
16.删去正整数列中的所有奇数的完全平方数,得到一个新数列,此新数列的第2004项是____.
三、解答题:(本大题6小题,共74分,必需写出必要的文字说明.推理过程或计算步骤.)
17.(本题满分12分)
同时抛掷15枚均匀的硬币一次.(1)试求至多有1枚正面向上的概率;(2)试问出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率是否相等?请说明理由.
18.(本题满分12分)
已知![]()
![]() ,函数
,函数![]() .
.
(1)将f(x)写成![]() 的形式,并求其图象对称中心的坐标;
的形式,并求其图象对称中心的坐标;
(2)如果△ABC的三边a,b,c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域.
19.(本题满分12分)
已知点H(0,―3),点P在x轴上,点Q在y轴正半轴上,点M在直线PQ上,且满足![]() ,
,![]() .
.
(1)当点P在x轴上移动时,求动点M的轨迹曲线C的方程;
(2)过定点A(a,b)的直线与曲线C相交于两点S、R,求证:抛物线S、R两点处的切
线的交点B恒在一条直线上.
20.(本题满分12分)
已知,如图四棱锥P—ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且AG=![]() GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为
GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P—BCG的体积为![]() .
.
(1)求异面直线GE与PC所成的角;
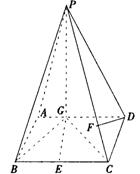 (2)求点D到平面PBG的距离;
(2)求点D到平面PBG的距离;
(3)若F点是棱PC上一点,且DF⊥GC,求![]() 的值.
的值.
21.(本题满分12分)
在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() 、
、![]() 两边所在的直线分别
两边所在的直线分别
与![]() 轴交于原点同侧的点
轴交于原点同侧的点![]() 、
、![]() ,且满足
,且满足![]() (
(![]() 为不
为不
等于零的常数).
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)如果存在直线![]()
![]() ,使
,使![]() 与点
与点![]() 的轨迹相交于不同的
的轨迹相交于不同的![]() 、
、![]() 两点,且
两点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
22.(本题满分14分)
设数列![]() 满足:若
满足:若![]() ;若
;若![]() .
.
(1)求:![]() ;
;
(2)若![]() ,求证:
,求证:![]() ;
;
(3)证明:![]() .
.
参考答案
一、选择题
1.B 2.B 3.D 4.C 5.B 6.D 7.B 8.A 9.C 10.A 11.B 12.C
二、填空题
13.![]() 14.a>0,b<0,c<0,d=0 15.
14.a>0,b<0,c<0,d=0 15.![]() 16.2027
16.2027
[解析]:注意到:![]()
故前2004项共删去22个数,又因为2004与2026间还有一个需要删去的2025,所以第2004项是2004+22+1=2027
三、解答题
17.(1)解:记“抛掷1枚硬币1次出现正面向上”为事件A,P(A)=![]()
抛掷15枚均匀的硬币一次相当于做15次独立的重复试验,
根据n次独立重复试验中事件A发生k次的概率公式,记至多有1枚正面向上的概率为P1,则P1=P(0)+P(1)=![]()
(2)解:记正面向上为奇数枚的概率为P2,记正面向上为偶数枚的概率为P3,则有
![]()
![]()
又“出现正面向上为奇数枚”的事件与“出现正面向上为偶数枚”的事件是对立事件
∴P3=1-![]() =
=![]() .
.
∴出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率相等.
18.解 (1)![]()
![]()
![]() .
.
令![]() =0,得
=0,得![]() .
.
而y=![]() 的图象可由
的图象可由![]() 向上平移
向上平移![]() 个单位得到,故所求对称中心的坐标为
个单位得到,故所求对称中心的坐标为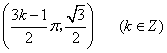 .
.
(2)由已知b2=ac,![]()
![]()
![]()
![]()
即![]() 的值域为
的值域为![]() .
.
综上所述,![]() ,
,![]() 值域为
值域为![]() .
.
19.(1)解:设P(a,0),Q(0,b)则:![]() ∴
∴![]()
设M(x,y)∵![]() ∴
∴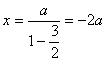
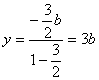 ∴
∴![]()
(2)解法一:设A(a,b),![]() ,
,![]() (x1≠x2)
(x1≠x2)
则直线SR的方程为: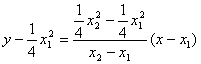 ,即4y = (x1+x2)x-x1x2
,即4y = (x1+x2)x-x1x2
∵A点在SR上,∴4b=(x1+x2)a-x1x2 ① 对![]() 求导得:y′=
求导得:y′=![]() x
x
∴抛物线上S.R处的切线方程为
![]() 即4
即4![]() ②
②
![]() 即4
即4![]() ③
③
联立②、③得 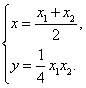
代入①得:ax-2y-2b=0故:B点在直线ax-2y-2b=0上.
解法二:设A(a,b),当过点A的直线斜率不存在时l与抛物线有且仅有一个公共点,与题意不符,可设直线SR的方程为y-b=k(x-a).
与![]() 联立消去y,得x2-4kx+4ak-4b=0.设
联立消去y,得x2-4kx+4ak-4b=0.设![]() ,
,![]() (x1≠x2)
(x1≠x2)
则由韦达定理,得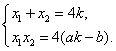
又过S、R点的切线方程分别为![]() ,
,![]() .
.
联立,并解之,得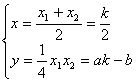 (k为参数) 消去k,得ax-2y-2b=0.
(k为参数) 消去k,得ax-2y-2b=0.
故B点在直线2ax-y-b=0上.
20.解法一:
(1)由已知![]() ,∴PG=4.
,∴PG=4.
如图所示,以G点为原点建立空间直角坐标系o—xyz,
则B(2,0,0),C(0,2,0),P(0,0,4),故E(1,1,0).
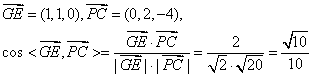
∴异面直线GE与PC所成的角为arccos![]() .
.
(2)平面PBG的单位法向量![]() .
.
![]()
∴点D到平面PBG的距离为![]() .
.
(3)设F(0,y,z),
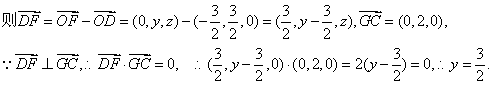
在平面PGC内,过F点作FM⊥GC,M为垂足,则![]() .
.
![]() .
.
解法二:
(1)由已知![]() ,∴PG=4.
,∴PG=4.
在平面ABCD内,过C点作CH//EG,交AD于H,连结PH,则∠PCH(或其补角)就是异面直线GE与PC所成的角.
在△PCH中,![]() ,由余弦定理得,cos∠PCH=
,由余弦定理得,cos∠PCH=![]()
∴异面直线GE与PC所成的角为arccos![]()
(2)∵PG⊥平面ABCD,PG![]() 平面PBG ∴平面PBG⊥平面ABCD
平面PBG ∴平面PBG⊥平面ABCD
在平面ABCD内,过D作DK⊥BG,交BG延长线于K,则DK⊥平面PBG
∴DK的长就是点D到平面PBG的距离.
![]() 在△DKG,DK=DGsin45°=
在△DKG,DK=DGsin45°=![]()
∴点D到平面PBG的距离为![]() .
.
(3)在平面ABCD内,过D作DM⊥GC,M为垂足,连结MF,又因为DF⊥GC
∴GC⊥平面MFD, ∴GC⊥FM.
由平面PGC⊥平面ABCD,∴FM⊥平面ABCD,∴FM//PG.
由GM⊥MD,得GM=GD·cos45°=![]() .
.
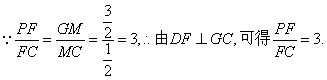
21.解:(1)设点![]() ,
,![]() .
.
当![]() 时,
时,![]() 轴,当
轴,当![]() 时,
时, ![]() 轴,与题意不符,所以
轴,与题意不符,所以![]() ;
;
由![]() .
.![]() .
.![]() 三点共线有
三点共线有![]() ,解得
,解得![]() .
.
同理由![]() .
.![]() .
.![]() 三点共线,解得
三点共线,解得![]() .
.
![]() ,
, ![]() ,
,
化简得点![]() 的轨迹方程为
的轨迹方程为![]() .
.
(2)设![]() 的中点为
的中点为![]() ,
,
![]()
![]() ,
,
由![]() ,
,
化简得 ![]() …①
…①
![]() ,
,![]() .
.
![]() ,即
,即![]() ,
,
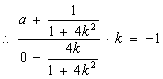 ,
,![]() ,即
,即![]() ………②
………②
![]()
![]() ,
, ![]()
![]() .把②代入①并化简得
.把②代入①并化简得![]()
![]() .
.
当![]() 时,直线
时,直线![]() 过点B,而曲线C不过点B,所以直线
过点B,而曲线C不过点B,所以直线![]() 与曲线C只有一个公共点.故
与曲线C只有一个公共点.故![]() 舍去;故
舍去;故![]() 的取值范围是
的取值范围是![]() 且
且![]() .
.
22.解:(1)![]() =22;
=22;
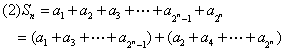

(3)由(2)知![]()
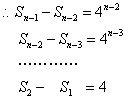
![]() =
=![]()
![]()
![]() .
.