南昌十六中2005-2006年高三周练卷（3）
2005-9-21
一、单择题（本题每小题5分，共60分）
1．长方体A1B1C1D1-ABCD的底边BC的中点是M，则过A,M,D1的截面是 （ ）
(A)三角形 (B)四边形 (C)五边形 (D)六边形
2．已知点P分有向线段
的比为–2，且A(1 , 5), B( 2 , 3 ), 则点P的位于 ( )
A．第一象限 B.第二象限 C.第四象限 D.坐标轴上
3．已知向量
，
．若
不超过5，则k的取值范围是
（
）
A． [－4，6] B． [－6，4] C． [－6，2] D． [－2，6]
4．在长方体ABCD—A1B1C1D1中，B1C和C1D与底面ABCD所成的角分别是600和450，则异面直线B1C与C1D所成角的余弦值是（ ）
（A）
（B）
（C）
（D）
5.把函数y=f(x)的图象沿直线x+y=0的方向向右下方平移2
个单位，得到函数
ｙ＝log２ｘ的图象，则
A.f(x)=log２（ｘ＋２）＋２ B. f(x)=log２（ｘ-２）＋２
C. f(x)=log２（ｘ＋２）－２ D. f(x)=log２（ｘ-２）－２
6．在复平面内，设向量
等于（ ）
A．
B．
C．
（）
D．（）
7．正方体ABCD－A1B1C1D1中，E、F分别为棱AB、C1D1的中点，则直线A1B1与平面A1ECF所成角的正弦为（ ）
A． B． C． D．
8．已知函数f(x)＝x3+ax2，过曲线y＝f(x) 上一点P(－1，b) 且平行于直线3x+y＝0的切线方程为（ ）
A．3x+y－1＝0 B．3x+y+1＝0 C．3x－y＋1＝0 D．3x+y－2＝0
9．已知向量
＝(，0)，
＝(，)，
＝(cosa，sina)(a∈R)，则
与夹角的取值范围是（ ）
A．[0，] B．[，] C．[，] D．[，]
10．平面向量
则这样的向量
有（ ）
A．1个 B．2个
C．多个2个 D．不存在
11.已知如图∠Ｃ＝９０°，AC=BC,M、N分别为BC和AB的中点，沿直线MN将△BMN折起，使二面角Ｂ′－MN－Ｂ为60°，则斜线Ｂ′Ａ与平面ABC所成角的正切值为
A.
B.
C. 
D.
12、如图是一个无盖正方体盒子的表面展开图，A、B、C为
其上的三个点，则在正方体盒子中，∠ABC等于（ ）
（A）45° （B）120° （C）90° （D）60°
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
二、填空题（本题每小题4分，共16分）
13. 与向量
垂直的单位向量坐标为 ．
14．已知球面上A、B两点间的球面距离是1，过这两点的球面半径的夹角为60°，则这个球的表面积与球的体积之比是 .
15．过正方体A1B1C1D1-ABCD的底面对角线AC，作与底面成450角的截面，把正方体分成两部分，则这大、小两部分的体积之比是
16．在一个棱长为
的正四面体内有一点P，它到三个面的距离分别是1cm，2cm，3cm，则它到第四个面的距离为_______________cm。
三、解答题（本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤）：
17．（本小题满分12分）A、B、C为△ABC的三内角，且其对边分别为a、b、c。若
＝(－cos，sin)，
＝(cos，sin)，且·＝.
（1）求A；
（2）若a＝2，三角形面积S＝，求b+c的值.
18．（本小题满分12分）编号为1，2，3的三位学生随意入坐编号为1，2，3的三个座位，每位学生坐一个座位。设与座位编号相同的个数为x．
（1）求随机变量x的概率分布；
（2）求随机变量x的数学期望和方差．
19．（本小题满分12分）如图，在底面是矩形的四棱锥P—ABCＤ中，PA⊥平面ABCＤ PA=AB=1，BC=2。
（1）求证：平面PDC⊥平面PAD；
（2）若E是PD的中点，求异面直线AE与PC所成角的余弦值；
（3）在BC边上是否存在一点G，使得D点到平面PAG的距离为1，若存在，求出BG的值；若不存在，请说明理由。
20.（本小题满分12分）
已知三棱锥P－ＡＢＣ中，PC⊥底面ABC，ＡＢ＝ＢＣ，Ｄ、Ｅ、F分别为AC、PA、PC的中点，DE⊥ＡＰ于E.
（Ⅰ）求证：ＡＰ⊥平面BDE；
（Ⅱ）求证：平面ＢＤＥ⊥平面ＢＤＦ；
（Ⅲ）若AE∶ＥＰ＝１∶２，求截面BEF分三棱锥Ｐ－ＡＢＣ所成两部分的体积比.
21．（本小题满分12分）
已知定点
（Ⅰ）求动点P的轨迹方程，并说明方程表示的曲线；
（Ⅱ）当
的最大值和最小值.
22．（本小题满分14分）
若F1、F2分别为双曲线 －＝1下、上焦点，O为坐标原点，P在双曲线的下支上，点M在上准线上，且满足：
，
(l>0)。
(1)求此双曲线的离心率；
(2)若此双曲线过N(，2)，求此双曲线的方程
(3)若过N(，2)的双曲线的虚轴端点分别B1，B2(B2在x轴正半轴上)，点A、B在双曲线上，且
，求
时，直线AB的方程。
参考答案及部分解答
一、选择题（每小题5分，共60分）：
BBC？B DABCA BC
6．D 
10
直线与圆相切.
二、填空题（每小题4分，共16分）
13． 
； 14． p； 15．1 ； 16．4
三、解答题（共74分，按步骤得分）
17.解：（1）∵＝(－cos，sin)，＝(cos，sin)，且·＝，
∴－cos2＋sin2＝，………………………………………………2分
即－cosA＝，又A∈(0，p)，∴A＝p………………………………5分
（2）S△ABC＝bc·sinA＝b·c·sinp＝
，∴bc＝4 …………………7分
又由余弦定理得：a2=b2+c2－2bc·cos120°＝b2+c2+bc ………………10分
∴16＝(b+c)2，故b+c＝4.……………………………………………12分
18. 解：（1）P(x＝0)＝＝，P(x＝1)＝＝，
P(x＝2)＝0，P(x＝3)＝＝……………………………………………4分
| x | 0 | 1 | 2 | 3 |
| P | 0 |
|
（2）Ex＝1×+3×＝1…………………………………………………9分
Dx＝(1－0)2×+(1－1)2×+(1－2)2×0+(3－1)2×＝1…………12分
19. 解：以A为原点，AB所在直线为x轴，AD所在直线为y轴，AP所在直线为z轴建立空间直角坐标系，则A(0，0，0)，B(1，0，0)，C(12，0，)，D(0，2，0)，E(0，1，)，P(0，0，1)。
∴
＝(－1，0，0)，
＝(0，2，0)，
＝(0，0，1)，
＝(0，1，) ，
＝(1，2，－1)，
(1) 
平面PDC⊥平面PAD.……4分
(2)∵cos
＝＝，
∴所求角的余弦值为。………………………………………………………………8分
(3)假设BC边上存在一点G满足题设条件，令BG＝x，则G(1，x，0)，作DQ⊥AG，则DQ⊥平面PAG，即DQ＝1。∵2S△ADG＝S矩形ABCD，∴
＝2∴
＝2，又AG＝，∴x＝<2，
故存在点G，当BG＝时，使点D到平面PAG的距离为1。………………………………12分
22.解： (1) 
，∴PF1OM为平行四边形，
又知M在∠PF1O的角平分线上，
∴四边形PF1OM为菱形，且边长为
＝c…………………………………2分
∴
＝2a+
＝2a+c，由第二定义＝e即＝e，∴+1＝e且e>1
∴e=2…………………………………………………………………………………4分
(2)由e=2，∴c=2a即b2=3a2，双曲线方程为 －＝1
又N(，2)在双曲线上，∴－＝1，∴a2＝3∴双曲线的方程为－＝1…7分
(3)由知AB过点B2，若AB⊥x轴，即AB的方程为x=3，此时AB1与BB1不垂直；设AB的方程为y=k(x－3)代入－＝1得
(3k2－1)x2－18k2x+27k2－9=0………………………………………………9分
由题知3k2－1≠0且△>0即k2> 且k2≠，
设交点A(x1，y1)，B(x2，y2)，
＝(x1+3，y1)，
＝(x2+3，y2)，
∵，∴
＝0即x1x2+3(x1+x2)+9+y1y2＝0………………11分
此时x1+x2＝，x1·x2=9，
y1y2＝k2(x1－3) (x2－3)＝k2[x1x2－3(x1+x2)+9]= k2[18－]＝－
∴9＋3＋9－＝0，∴5 k2＝1，∴k＝±
∴AB的方程为y=±(x－3) .………………………………………………14分
21（I）设动点的坐标为P(x,y),则
|
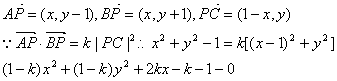
若k=1，则方程为x=1，表示过点（1，0）是平行于y轴的直线.（4分）
若k≠1，则方程化为：
为半径的圆.
（5分）
（II）当k=2时，方程化为（x－2）2+y2=1 .
20.（Ⅰ）证明：∵PC⊥底面ABC，BD
平面ABC，
∴PC⊥BD，由AB＝BC，D为AC的中点，
得BD⊥AC，又PC∩AC＝C，∴BD⊥平面PAC 2分
又PA平面PAC，∴BD⊥PA，由已知DE⊥PA，PE∩BD＝D，
∴AP⊥平面BDE 4分
(Ⅱ)证明：由BD⊥平面PAC，DE平面PAC，得BD⊥DE，由D、F分别为AC、PC的中点
∴DF∥AP，又由已知DE⊥AP，∴DE⊥DF 6分
BD∩DF＝D，∴DE⊥平面BDF，又DE平面BDE，∴平面BDE⊥平面BDF
8分
(Ⅲ)解：设点E和点A到平面PBC的距离分别为ｈ１和ｈ２
则ｈ１∶ｈ２＝ＥP∶AP＝２∶３ 9分
∴
11分
所以截面BEF分三棱锥P－ABC所成两部分体积比为１∶２或（２∶１） 12分