高三数学第二次月考检测
第一卷
一. 填空题:共15小题,每题4分
1. 已知集合![]() ,
,![]() ,则与
,则与![]() 等价的
等价的![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. ![]() 、
、![]() 是两个不等实数,则
是两个不等实数,则![]() 所有可能取到的值组成的集合为( )
所有可能取到的值组成的集合为( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
3. 关于![]() 的方程
的方程![]() 有且只有两个实根,则
有且只有两个实根,则![]() 不可能是( )
不可能是( )
A. 一次函数 B. 二次函数 C. 对数函数 D. 指数函数
4. ![]() 过定点(1,0)则
过定点(1,0)则![]() 必过定点( )
必过定点( )
A.(0,1) B.(2,0) C.(2,1) D. (![]() ,1)
,1)
5. 已知![]() ,且
,且![]() ,则
,则 的值( )
的值( )
A. 等于![]() B.
等于
B.
等于![]()
C. 等于![]() D.
以上都不对
D.
以上都不对
6. 甲、乙、丙三人加工某一种零件,合格的概率分别为0.8,0.75,0.6,现同时各加工一个该种零件,至多有一个是不合格品的概率是( )
A. 0.85 B. 0.45 C. 0.81 D. 以上都不对
7. 若![]() ,则关于
,则关于![]() 的说法:(1)为奇函数,且有两个极值点;(2)为奇函数,且在
的说法:(1)为奇函数,且有两个极值点;(2)为奇函数,且在![]() 上单减;(3)为奇函数,且值域为
上单减;(3)为奇函数,且值域为![]() 。
。
其中正确的有( )
A. 3个 B. 2个 C. 1个 D. 0个
8. ![]() 是R上的奇函数,且对一切
是R上的奇函数,且对一切![]() 总有
总有![]() ,若
,若![]() ,则下列各点:(1)(
,则下列各点:(1)(![]() ,
,![]() );(2)(
);(2)(![]() ,
,![]() );(3)(
);(3)(![]() ,
,![]() );(4)(
);(4)(![]() ,0)(
,0)(![]() )。其中在
)。其中在![]() 的图象上的有( )
的图象上的有( )
A. 1个 B. 2个 C. 3个 D. 4个
9. ![]() ,
,![]() (
(![]() ),则
),则![]() ( )
( )
A. 3 B. 0 C. 15 D. 2
10. ![]() 存在反函数
存在反函数![]() ,则:(1)
,则:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 中,一定能表达
中,一定能表达![]() 的反函数的有( )
的反函数的有( )
A.(1)和(2) B. 只有(2) C.(2)和(3) D. 只有(3)
11. 设不等式![]() 与
与![]() 的解集分别为A、B,且
的解集分别为A、B,且![]() ,则
,则![]() 、
、![]() 的值分别为( )
的值分别为( )
A. 2,5 B. ![]() ,5 C. 2,
,5 C. 2,![]() D.
D. ![]() ,
,![]()
12. 若![]() ,
,![]() 的充要条件是( )
的充要条件是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() 或
或![]()
13. ![]() 对一切
对一切![]() 成立,则
成立,则![]() 的范围是( )
的范围是( )
A. ![]() 或
或![]() B.
B.
![]() 或
或![]()
C. ![]() D.
D.
![]()
14. ![]() 为R上单增的函数,且方程
为R上单增的函数,且方程![]() 与
与![]() 的两个根分别是
的两个根分别是![]() 、
、![]() ,则
,则![]() 的值( )
的值( )
A. 等于![]() B. 等于
B. 等于![]() C. 等于0 D. 无法确定
C. 等于0 D. 无法确定
15. 设![]() ,
,![]() ,
,![]()
![]() ,命题
,命题![]() :若
:若![]() ,则
,则![]() 或
或![]() ;命题
;命题![]() :
:![]() 或
或![]() 。则使得“
。则使得“![]() 或
或![]() ”为真命题,“
”为真命题,“![]() 且
且![]() ”为假命题的
”为假命题的![]() 的集合是( )
的集合是( )
A. ![]() B.
B.
![]()
C. ![]() D.
以上都不对
D.
以上都不对
第二卷
二. 填空题:共6小题,每小题5分
16. ![]() 的值域是
的值域是![]() ,则它的定义域为
。
,则它的定义域为
。
17. 若关于![]() 的方程
的方程![]() 有且只有一个实根,则实数
有且只有一个实根,则实数![]() 的取值集合为
。
的取值集合为
。
18. 已知![]() ,若存在
,若存在![]() ,使
,使![]() ,则
,则![]() 的取值范围是
。
的取值范围是
。
19. 已知![]() ,
,![]() ,则
,则![]() 与2的大小关系是 。
与2的大小关系是 。
20. ![]() 是实数
是实数![]() 、
、![]() 的等差中项,
的等差中项,![]() 是
是![]() 、
、![]() 的等比中项,则
的等比中项,则![]() 的范围是 。
的范围是 。
21. 奇函数![]() 存在反函数
存在反函数![]() ,对
,对![]() 与
与![]() 的图象的下列说法:(1)关于原点对称;(2)关于
的图象的下列说法:(1)关于原点对称;(2)关于![]() 对称;(3)关于
对称;(3)关于![]() 对称;(4)原点必是一个公共点;(5)可能有无穷多个公共点。其中正确的是
。(将你认为正确的说法前面的序号全都填入横线的上方)。
对称;(4)原点必是一个公共点;(5)可能有无穷多个公共点。其中正确的是
。(将你认为正确的说法前面的序号全都填入横线的上方)。
三. 解答题:共5小题,每小题12分
22. 已知:![]() ,
,
(1)判断2001、2002、2003是否属于A;
(2)若![]() 且
且![]() ,求证:
,求证:![]() 。
。
23. 若不等式![]() 的解集为(4,b),求a、b的值。
的解集为(4,b),求a、b的值。
24. 已知A、B是复平面上两点,且A在第一象限的角分线上,O为原点。若它们满足:
(1)![]() ;(2)
;(2)![]() 的面积S=9,求这两点所对应的复数。
的面积S=9,求这两点所对应的复数。
25. 已知![]() ,当
,当![]() 时,值域亦为
时,值域亦为![]() 。求证:
。求证:![]() 的解集仍为
的解集仍为![]() 。
。
26. 已知![]() 。如对任意
。如对任意![]() 都有
都有![]() ,试求出实数
,试求出实数![]() 的取值范围。
的取值范围。

【试题答案】
第一卷
一.
1. D 2. D 3. D 4. D 5. C 6. C 7. C 8. D 9. C 10. D
11. A 12. D 13. B 14. A 15. C
第二卷
16. ![]() 17.
17. ![]() 18.(
18.(![]() ,
,![]() )
)
19. ![]() 20.
20. ![]()
21.(2)(3)(5)
三.
22.
(1)证法1:
先确定集合A,对任![]()
① 若m,n的奇偶性相同,则![]() 是4的倍数
是4的倍数
如果m,n同为奇数,设![]() ,
,![]() (
(![]() 、
、![]() )
)
则![]()
如果m,n同为偶数,设![]() ,
,![]() (
(![]() ,
,![]() )
)
则![]()
② 若m,n的奇偶性相反,则![]() 是奇数
是奇数
如果m为奇数,n为偶数,设![]() ,
,![]()
则![]() 为奇数
为奇数
如果m为偶数,n为奇数,同理![]() 为奇数
为奇数
反之,可证4的倍数或奇数均为A中的元素
<1> 若![]() (
(![]() ),设
),设![]() ,令
,令
![]() 即
即![]() ,故
,故![]()
<2> 若![]() (
(![]() ),设
),设![]()
令![]() 即
即![]() 故
故![]()
综上可知:![]() 或
或![]() ,
,![]()
所以有:2001、2003![]() ,但2002
,但2002![]()
(2)若![]() 且
且![]() ,则
,则![]() 、
、![]() 或均为奇数或至少有一个为4的倍数
或均为奇数或至少有一个为4的倍数
① 若![]() 、
、![]() 均为奇数,则
均为奇数,则![]() 为奇数,故
为奇数,故![]()
② 若![]() 、
、![]() 中至少有一个为4的倍数,则
中至少有一个为4的倍数,则![]() 为4的倍数,故
为4的倍数,故![]() ,综上所述
,综上所述![]()
证法2:
(1)设![]() 即
即![]()
则![]() 为4的倍数或为奇数,故2002
为4的倍数或为奇数,故2002![]() ,而由
,而由![]()
![]() 则
则![]() ,
,![]()
(2)若![]() ,
,![]() ,设
,设![]() ,
,![]()
则![]()
![]()
![]()
23.
解法1:设![]() ,则原不等式
,则原不等式![]() ,
,![]()
条件转化为不等式![]() ,(
,(![]() )的解集为(2,
)的解集为(2,![]() )
)
设![]() ,如图,
,如图,

条件即


或用韦达定理,由![]() ,
,![]()
解法2:令![]() ,
,![]() ,如图
,如图![]()
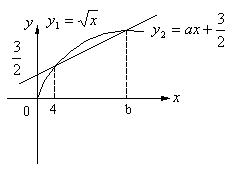
由![]() 又由
又由![]()
24. 设![]()
![]()
![]()
又已知![]() ,上面等号均成立
,上面等号均成立
此时,![]() 即
即![]() 为
为![]()
等腰直角三角形,又由A在第一象限角平分线上,且![]()
则![]() ,又OA⊥OB,OA=OB
,又OA⊥OB,OA=OB
则![]() 或
或![]()

25.
证法1:![]() ,则
,则![]() ,故一元二次函数
,故一元二次函数![]() 在
在![]() 上是增函数,故
上是增函数,故![]() 即a、b是
即a、b是![]() 的两个实根
的两个实根
由![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
故![]() 得证。
得证。
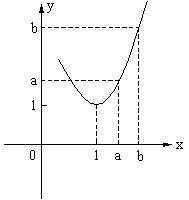
证明2:同上可得![]() ,
,![]() ,由
,由![]() ,同理
,同理![]()
即a,b也是方程![]() 的两个根
的两个根
设![]() ,
,![]() ,则
,则![]()
即![]()
也可![]()
![]()
![]()

列表如下:
|
| ( |
| ( |
|
| — | 0 | + |
|
|
| 极小 |
|
又![]() ,
,![]() ,则
,则![]() 解集为
解集为![]()
证法3:同证法(1)可得![]() ,
,![]()
即1,3为![]() 的根,则
的根,则![]()
![]()
![]()
![]()
又由![]() ,
,![]()
故![]()
![]()
![]()
则![]() 得证
得证
证法4:同(1)可得![]() ,
,![]() ,设
,设![]() ①
①
则![]() ②
②
①—②得:![]()
![]() 0
0
由![]() 则上式等价于
则上式等价于![]()
即![]() 整理得:
整理得:![]()
故![]()
26. 解:
由对任![]() 都有
都有![]()
故
又由![]()
则![]()

![]() 或
或![]()
即![]() 的取值范围是
的取值范围是![]()
