江苏省淮阴中学高三数学综合练习（一）2006.3.9
一、选择题：
1．已知三角形的内角分别是A、B、C，若命题
,命题
，则P是Q的 （ ）
(A)充分而不必要条件 (B)必要而不充分条件
(C )充要条件 (D)既不充分也不必要条件
2．设直线
ax＋by＋c＝0的倾斜角为
，且sin＋cos＝0，则a，b满足 （ ）
A．
B．
C．
D．
3．已知椭圆
的离心率 e＝
， 则m的值为
（ ）
A．3 B．或3 C．
D．
或
4．已知实数
满足
．命题P：函数
在区间[0，1]上是减函数． 命题Q：
是
的充分不必要条件．则
（ ）
A．“P或Q”为真命题； B．“P且Q”为假命题；
C．“┐P且Q”为真命题； D．“┐P或┐Q”为真命题
5．教师想从52个学生中抽取10名分析期中考试情况，一小孩在旁边随手拿了两个签，教师没在意，在余下的50个签中抽了10名学生．则其中的李明被小孩拿去和被教师抽到的概率分别为 （ ）
A．
B．
C．
D．
6．设
是函数
的反函数，若
，则
的值为
（ ）
A．1
B．2
C．3
D．
7．两条异面直线a和b上分别有5和4个点，从中任选4点作为顶点组成一个四面体的，这样的四面体的个数为 （ ）
（A）
（B）
（C）
（D）
8．三棱锥
中，
两两垂直，且
，
，则此三棱锥的体积
（ ）
(A) 有最大值3，无最小值； (B) 有最小值3，无最大值；
(C) 有最大值9，无最小值； (D) 无最大值，也无最小值；
9．
是曲线
上任意一点，则
的最大值是（ ）
（A）36
（B）、6
（C）、26
（D）、25
10．α、β为两个确定的相交平面,
a、b为一对异面直线,下列条件:：① a∥α, b
β; ② a⊥α, b∥β; ③ a⊥α, , b⊥β; ④ a∥α, b∥β且a与α的距离等于b与β的距离. 其中能使a、b所成的角为定值的有
（ ）
（A）. 0个 （B）. 1个 （C）. 2个 （D）. 3个
11．若函数
的反函数为
，则函数
与函数
的图象 （ ）
A．关于直线
对称 B．关于直线
对称
C．关于直线
对称 D．关于直线
对称
12．某商场宣传在“五一黄金周”期间对顾客购物实行一定的优惠，商场规定： ①如一次性购物不超过200元，不予以折扣； ②如一次性购物超过200元但不超过500元的，按标价给予九折优惠；③如一次性购物超过500元的，其中500元给予9折优惠，超过500元的部分给予八五折优惠．某人两次去购物，分别付款176元和432元，如果他只去一次购买同样的商品，则应付款 （ ）
A．608元 B．574.1元 C．582.6元 D．456.8元
二、填空题：
13．有两个相同的直三棱柱,高为
,底面三角形的三边长分别为3a、4a、5a(a>0).用它们拼成一个三棱柱或四棱柱,在所有可能的情况中,全面积最小的是一个四棱柱,则a的取值范围是
．
14．给出下列图象
其中可能为函数f(x)＝
＋ax3＋bx2＋cx＋d(a，b，c，d∈R)的图象的是_____．
15．已知
为实数，
展开式中
的系数为
，则
．
16。若函数
的图象关于直线
对称，则
=
三、解答题：
17．平面直角坐标系中有点
,
，且
.
（Ⅰ）求向量
与
的夹角
的余弦值用
表示的函数
；
（Ⅱ）求的最值。
18．已知数列
、
（Ⅰ）若{an}是等比数列，试求数列{bn}的前n项和Sn的公式；
（Ⅱ）当{bn}是等比数列时，甲同学说：{an}一定是等比数列；乙同学说：{an}一定不是等比数列,你认为他们的说法是否正确？为什么？
19．在
中，已知
，
，
、
两边所在的直线分别与轴交于原点同侧的点
、
，且满足
（为不等于零的常数）．
（1）求点
的轨迹方程；
（2）如果存在直线
，使
与点
的轨迹相交于不同的
、
两点，且
，求的取值范围．
20．设
，
为直角坐标平面内x轴．y轴正方向上的单位向量，若
，且
（Ⅰ）求动点M(x,y)的轨迹C的方程；
（Ⅱ）设曲线C上两点A．B，满足(1)直线AB过点（0，3），(2)若
，则OAPB为矩形，试求AB方程
21．一个多面体的直观图，前视图（正前方观察），俯视图（正上方观察），侧视图（左侧正前方观察）如下所示。
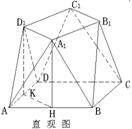（1）求
与平面
所成角的大小及
面
与面所成二面角的大小；
（2）求此多面体的表面积和体积。
 |
22．由原点O向三次曲线y=x3－3ax2＋b x (a≠0)引切线,切于不同于点O的点P1(x1,y1),再由P1引此曲线的切线,切于不同于P1的点P2(x2,y2),如此继续地作下去,……,得到点列
{ P n(x n , y n)},试回答下列问题:
（Ⅰ）求x1;
（Ⅱ）求x n与x n+1的关系;
（Ⅲ）若a>0,求证:当n为正偶数时, x n<a;当n为正奇数时, x n>a.
参考答案
一．选择题：
CDBAB BCAAB BC
二．填空题：
13．．0<a<
， 14。①③；15。
；16.6
三．解答题
17．Ⅰ）
x∈[
] .
6分
（Ⅱ）
10分
即
又
， 
18．（I）解：因为{an}是等比数列a1=1,a2=a.
∴a≠0，an=an－1.
又
即
是以a为首项, a2为公比的等比数列.
（II）甲、乙两个同学的说法都不正确，理由如下：
解法一：设{bn}的公比为q，则
又a1=1,a2=a, a1, a3, a5,…，a2n－1，…是以1为首项，q为公比的等比数列，
a2, a4, a6, …, a2n , …是以a为首项，q为公比的等比数列，
即{an}为：1，a, q, aq , q2, aq2,
当q=a2时，{an}是等比数列；
当q≠a2时，{an}不是等比数列.
解法二：{an}可能是等比数列，也可能不是等比数列，举例说明如下：
设{bn}的公比为q
（1）取a=q=1时，an=1(n∈N)，此时bn=anan+1=1, {an}、{bn}都是等比数列.
（2）取a=2, q=1时，
所以{bn}是等比数列，而{an}不是等比数列．
19．解：（1）设点
，
．
当
时，
轴，当
时， 
轴，与题意不符，所以
;
由
．．
三点共线有
，解得
．
同理由
．．
三点共线，解得
．
， 
，
化简得点的轨迹方程为
．
（2）设
的中点为
，
，
由
，
…①
，
．
，即
， 
，
，即
………②
， 
．把②代入①并化简得
．
当
时，直线
过点B，而曲线C不过点B，所以直线与曲线C只有一个公共点.故舍去;故
的取值范围是
且
．
20．（Ⅰ）解：令
则
即
即
又∵
∴
……………………3（分）
所求轨迹方程为
…………………………………………6（分）
（Ⅱ）解：由条件（2）可知OAB不共线，故直线AB的斜率存在
设AB方程为
则
………………………8（分）
∵OAPB为矩形，∴OA⊥OB 
……………………10（分）
∴
得
所求直线方程为
……………………………12（分）
21．解：（1）由已知图可得，平面
平面，取
中点
，连接
，
在等腰
中有
，则
平面，
是与平面所成角，
，∴
取
中点
，连接
，同理有
平面，即
是
在
平面内的射影，在中，
，
又
，设面与面所成二面角的大小为，则
∴面与面所成二面角的大小为
。
（2）此多面体的表面积
此多面体的体积
22．(1)由y=x3－3ax2＋b x, ①
得y′=3x2－6ax＋b.
过曲线①上点P1(x1, y1)的切线l1的方程是
由它过原点,有
4分
(2)过曲线①上点Pn+1(xn+1,yn+1)的切线ln+1的方程是
由ln+1过曲线①上点P n(x n, yn),有
∵x n－xn+1≠0,以x n－xn+1除上式,得
以x n－xn+1除之,得x n＋2xn+1－3a=0.
9分
(3)解法1 由(2)得
故数列{x n－a}是以x 1－a=为首项,公比为－的等比数列,
∵a>0,∴当n为正偶数时, 
当n为正奇数时, 
14分
解法2 
=
=
==
=
=
.以下同解法1.