德阳中学高三数学(10月)月考测试题(理科)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.已知集合![]() ,集合
,集合![]() ,则
,则![]() 是
是
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
2.已知命题p:函数![]() 的值域为R.命题q:函数
的值域为R.命题q:函数![]()
是R上的减函数.若p或q为真命题,p且q为假命题,则实数a的取值范围是
A.a≤1 B.a<2 C.1<a<2 D.a≤1或a≥2
3.函数![]() 在闭区间[-3,0]上的最大值、最小值分别是 ( )
在闭区间[-3,0]上的最大值、最小值分别是 ( )
(A)1,-1 (B)1,-17 (C)3,-17 (D)9,-19
4.设函数![]() 的图象与
的图象与![]() 的图象关于直线
的图象关于直线![]() 对称,
对称,
那么![]() 值等于
值等于
(A)-1 (B)-2 (C)![]() (D)
(D)![]()
5. 设函数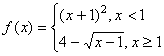 ,则使得
,则使得![]() 的自变量
的自变量![]() 的取值范围为
的取值范围为
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6.一元二次方程![]() 有一个正根和一个负根的充分不必要条件是:
有一个正根和一个负根的充分不必要条件是:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知函数![]() ,则
,则
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
8.设函数![]() 是定义在R上的奇函数,对于任意
是定义在R上的奇函数,对于任意![]() ,
,![]() .当
.当![]()
时![]() 的值是
的值是
A.1 B.-1 C.![]() D.
D.![]()
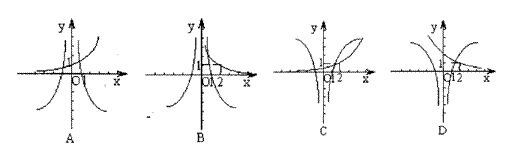
9. 已知![]() 则
则![]() 在同一坐标系内的图象大致是 ( )
在同一坐标系内的图象大致是 ( )
 |
10不等式 x2-5x+6≤x2-4 的解集
(A ) {x x≥2} (B) {x x≤2}
(C) {x x≥![]() }
(D)
}
(D) ![]()
11.已知函数y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域为[-π,π],且它们在x∈[0,π]上的图象如下图所示,则不等式![]() >0的解集为
>0的解集为

A.(-![]() ,0)∪(
,0)∪(![]() ,π) B.(-π,-
,π) B.(-π,-![]() )∪(
)∪(![]() ,π)
,π)
C.(-![]() ,0)∪(
,0)∪(![]() ,π) D.(-π,-
,π) D.(-π,-![]() )∪(0,
)∪(0,![]() )
)
(12) 某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下
| 行业名称 | 计算机 | 机械 | 营销 | 物流 | 贸易 |
| 应聘人数 | 215830 | 200250 | 154676 | 74570 | 65280 |
| 行业名称 | 计算机 | 营销 | 机械 | 建筑 | 化工 |
| 招聘人数 | 124620 | 102935 | 89115 | 76516 | 70436 |
若用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中数据,就业形势一定是( )
(A)计算机行业好于化工行业. (B) 建筑行业好于物流行业.
(C) 机械行业最紧张. (D) 营销行业比贸易行业紧张.
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.
13.函数![]() 的定义域是
,值域是
.
的定义域是
,值域是
.
14.当x=3时,不等式![]() 成立,则此不等式的解集是 .
成立,则此不等式的解集是 .
15.若不等式![]() 的解集
的解集![]() 是,设二次函数
是,设二次函数![]() 在区间
在区间![]() 的最大值为M,最小值为N,则M+N=__________________.
的最大值为M,最小值为N,则M+N=__________________.
16.函数![]() 是R上的单调函数且对任意的实数都有
是R上的单调函数且对任意的实数都有![]() .
.![]() 则不等式
则不等式![]() 的解集为__________________________.
的解集为__________________________.
德阳中学高三数学(10月)月考测试题(理科)
一. 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中, 只有一项是符合题目要求的, 把它选出来填下表中
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) |
二. 本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
(13)______________________;
(14)__________________;
(15)____________________;
(16)_____________________.
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)已知函数![]()
(1)若函数![]() 的图象关于原点对称,求
的图象关于原点对称,求![]() 的值;
的值;
(2)在(1)的条件下,解关于![]() 的不等式
的不等式![]()
18.(本题满分14分)
记函数f(x)=![]() 的定义域为A, g(x)=lg[(x-a-1)(2a-x)](a<1) 的定义域为B.
的定义域为A, g(x)=lg[(x-a-1)(2a-x)](a<1) 的定义域为B.
(1) 求A;
(2) 若B![]() A, 求实数a的取值范围.
A, 求实数a的取值范围.
19. (本小题满分12分)已知函数![]()
(1)
证明函数![]() 的图象关于点P
的图象关于点P![]() 对称.
对称.
(2)
求![]()
20(本小题满分12分)
函数![]() 是偶函数,且是周期为2的周期函数,当
是偶函数,且是周期为2的周期函数,当![]() 时,
时,![]() 在
在![]() 的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间[1,3]上,定点C的坐标为(0,
的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间[1,3]上,定点C的坐标为(0,![]() )(其中
)(其中![]() >2), 求ABC面积的最大值.
>2), 求ABC面积的最大值.
21. (12分)
某厂家拟在2003年国庆节期间举行促销活动,经调查测算,该产品的年销量(即该厂的年产量)x万件与年促销费用m万元(![]() )满足
)满足![]() (k为常数),如果不搞促销活动,该产品的年销售量只能是1万件,已知2003年生产该产品的固定投入为8万元,每生产1万件产品需要投入16万元,厂家将每件产品的销售价格定为年平均每件产品成本的1.5倍(产品成本包括固定投入和再投入两部分资金)
(k为常数),如果不搞促销活动,该产品的年销售量只能是1万件,已知2003年生产该产品的固定投入为8万元,每生产1万件产品需要投入16万元,厂家将每件产品的销售价格定为年平均每件产品成本的1.5倍(产品成本包括固定投入和再投入两部分资金)
(1)将2003年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2003年的促销费用投入多少万元时,厂家的年利润最大?
22.(本小题满分12分)
已知![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,且方程
上是减函数,且方程![]() 有三个根,它们分别为
有三个根,它们分别为![]() ,2,
,2,![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求证:![]() ;
;
(Ⅲ)求![]() 的取值范围.
的取值范围.
德阳中学高三数学(10月)月考测试题(理科答案)
一. 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中, 只有一项是符合题目要求的, 把它选出来填下表中
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) |
| C | c | C | B | A | C | B | B | B | A | D | B |
二. 本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
(13)[1,3];[0,2]; (14)(2,4);
(15)![]() ; (16)(-1,
; (16)(-1,![]() ).
).
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)已知函数![]()
(1)若函数![]() 的图象关于原点对称,求
的图象关于原点对称,求![]() 的值;
的值;
(2)在(1)的条件下,解关于![]() 的不等式
的不等式![]()
答: (1)
因为函数![]() 的图象关于原点对称
的图象关于原点对称
∴![]() ………………………2分
………………………2分
有![]()
化简得![]()
又∵![]() 不恒为0,∴
不恒为0,∴![]() ………………………6分
………………………6分
(2)由(1)知:![]() ,
,![]() ……………………………8分
……………………………8分
∵![]() ∈(-1,1)
∈(-1,1)
(Ⅰ)当![]() 时,不等式
时,不等式![]()
![]() 无解……………………………9分
无解……………………………9分
(Ⅱ)当![]() 时,解不等式
时,解不等式![]() 得大于失
得大于失![]() ………………11分
………………11分
(Ⅲ)当![]() 时,不等式的解
时,不等式的解![]() ………………………………12分
………………………………12分
18.(本题满分14分)
记函数f(x)=![]() 的定义域为A, g(x)=lg[(x-a-1)(2a-x)](a<1) 的定义域为B.
的定义域为A, g(x)=lg[(x-a-1)(2a-x)](a<1) 的定义域为B.
(1) 求A;
(2) 若B![]() A, 求实数a的取值范围.
A, 求实数a的取值范围.
解: (1)2-![]() ≥0, 得
≥0, 得![]() ≥0, x<-1或x≥1
≥0, x<-1或x≥1
即A=(-∞,-1)∪[1,+ ∞]…………………………………6分
(2) 由(x-a-1)(2a-x)>0, 得(x-a-1)(x-2a)<0.
∵a<1,∴a+1>2a, ∴B=(2a,a+1).
∵B![]() A, ∴2a≥1或a+1≤-1, 即a≥
A, ∴2a≥1或a+1≤-1, 即a≥![]() 或a≤-2, 而a<1,
或a≤-2, 而a<1,
∴![]() ≤a<1或a≤-2, 故当B
≤a<1或a≤-2, 故当B![]() A时, 实数a的取值范围是
A时, 实数a的取值范围是
(-∞,-2)∪[![]() ,1]………………………………………14分
,1]………………………………………14分
19. (本小题满分12分)已知函数![]() ,
,
(3)
证明函数![]() 的图象关于点P
的图象关于点P![]() 对称.
对称.
(4)
求![]()
答: (1)证明:函数的定义域为全体实数,在函数图象上任取一点Q![]() ,则
,则![]()
Q点关于![]() 的对称点
的对称点![]() …………………………………2分
…………………………………2分
则![]() ……………………………………3分
……………………………………3分
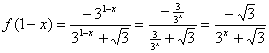 ………………………………………6分
………………………………………6分
∴![]() 即: 函数
即: 函数![]() 的图象关于点P
的图象关于点P![]() 对称…………7分
对称…………7分
(2)由(1)式得: ![]() ∴
∴![]() …………………9分
…………………9分
![]()
![]()
![]()
![]() =-3…………………………12分
=-3…………………………12分
20(本小题满分12分)
函数![]() 是偶函数,且是周期为2的周期函数,当
是偶函数,且是周期为2的周期函数,当![]() 时,
时,![]() 在
在![]() 的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间[1,3]上,定点C的坐标为(0,
的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间[1,3]上,定点C的坐标为(0,![]() )(其中
)(其中![]() >2), 求ABC面积的最大值.
>2), 求ABC面积的最大值.
解:∵函数![]() 是周期为2的周期函数, 当
是周期为2的周期函数, 当![]() 时,
时,![]()
∴当![]() 时,
时,![]()
又∵函数![]() 是偶函数,∴当
是偶函数,∴当![]() 时,
时,![]()
当 ![]() 时,
时,![]() …………………………4分
…………………………4分
不妨设A在B点的左边,设A(3-t,t), B(t+1,t) (![]()
AB=(t+1)-(3-t)=2t-2; ABC面积为S=![]()
即 ![]() ………………………8分
………………………8分
当![]() 即
即![]() , S有最大值.
, S有最大值. ![]()
当![]() 即
即![]() , S有最大值.
, S有最大值. ![]() …………………………………12分
…………………………………12分
21. (12分)
某厂家拟在2003年国庆节期间举行促销活动,经调查测算,该产品的年销量(即该厂的年产量)x万件与年促销费用m万元(![]() )满足
)满足![]() (k为常数),如果不搞促销活动,该产品的年销售量只能是1万件,已知2003年生产该产品的固定投入为8万元,每生产1万件产品需要投入16万元,厂家将每件产品的销售价格定为年平均每件产品成本的1.5倍(产品成本包括固定投入和再投入两部分资金)
(k为常数),如果不搞促销活动,该产品的年销售量只能是1万件,已知2003年生产该产品的固定投入为8万元,每生产1万件产品需要投入16万元,厂家将每件产品的销售价格定为年平均每件产品成本的1.5倍(产品成本包括固定投入和再投入两部分资金)
(1)将2003年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2003年的促销费用投入多少万元时,厂家的年利润最大?
. 解:(1)设2003年生产产品x万件
![]() 时,
时,![]() 代入
代入
![]() ………………(2分)
………………(2分)
则年成本:![]() ………………(4分)
………………(4分)
年利润:![]() …………(6分)
…………(6分)
![]() ……………………(7分)
……………………(7分)
(2)![]() ………………(10分)
………………(10分)
当且仅当![]() ,即
,即![]() 时取等号………………(11分)
时取等号………………(11分)
![]() 时,
时,![]() 万元……………………(12
万元……………………(12
22.(本小题满分12分)
已知![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,且方程
上是减函数,且方程![]() 有三个根,它们分别为
有三个根,它们分别为![]() ,2,
,2,![]() .
.
(Ⅰ)求![]() 的值;(Ⅱ)求证:
的值;(Ⅱ)求证:![]() ;(Ⅲ)求
;(Ⅲ)求![]() 的取值范围.
的取值范围.
答(1)![]() ,
, ![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数
上是减函数
∴当![]() 时,
时, ![]() 取得极大值.∴
取得极大值.∴![]() 即
即![]() ………………………4分
………………………4分
(2)由2是![]() 的根,∴
的根,∴![]() ,
,![]() ,
,![]() 的两个根分别为
的两个根分别为![]() ∵在
∵在![]() 上是减函数,∴
上是减函数,∴![]() ,即
,即![]()
![]() …………………8分
…………………8分
(3)由方程![]() 有三个根,它们分别为
有三个根,它们分别为![]() ,2,
,2,![]() .可设
.可设![]()
∴![]() 即:
即:![]() ,
,![]()
∴![]() =
=![]() ……………12分
……………12分