崇文区2005－2006学年度第二学期高三统一练习（二）
数学（理工农医类）
2006.5
本试卷分第一卷（选择题）和第二卷（非选择题）两部分。共150分。考试时间120分钟。
第一卷（选择题，共40分）
一、选择题：本大题共8小题，每小题5分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。
（1）已知
，若
，则
=（ ）
A.
B.
C.
D.
（2）将抛物线
的图象按向量a平移，使其顶点与坐标原点重合，则a=（ ）
A. （2，0） B. （－2，0）
C. （0，－2） D. （0，2）
（3）若
是（ ）
A. 第二象限角 B. 第一或第二象限角
C. 第三象限角 D. 第三或第四象限角
（4）双曲线
的一条渐近线与直线
垂直，则双曲线的离心率为（ ）
A.
B.
C.
D.
（5）用平面
截半径为R的球，如果球心到截面的距离为
，那么截得小圆的面积与球的表面积的比值为（ ）
A.
B.
C.
D.
（6）已知
的值为（ ）
A.
B.
C.
D.
（7）从1到100这100个整数中，从中任取两数，则所取的两数和为偶数的概率为（ ）
A.
B.
C.
D.
（8）a、b是任意实数，记
中的最大值为M，则（ ）
A.
M≥0 B.
C.
D.
第二卷（共110分）
二、填空题：本大题共6小题，每小题5分，共30分。把答案填在题中横线上。
（9）抛物线
的准线方程是________________。
（10）在数列
中，
，则此数列的前2006项之和为________________。
（11）设函数
，则f(x)的定义域是________________；f(x)的最小值是________________。
（12）如图，用红、黄、绿、橙、蓝五种颜色给图中三个方格涂色，每格涂一种颜色，相邻格涂不同颜色，则共有________________种涂色方案。
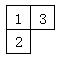
（13）已知函数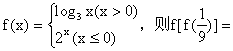
________________。
（14）若正实数a,b,c成等差数列，函数
的图象与x轴有两个交点，则
的符号是________________（填正或负），其取值范围是________________。
三、解答题：本大题共6小题，共80分。解答应写出文字说明，证明过程或演算步骤。
（15）（本小题共13分）
已知函数
。
（I）求函数f(x)图像的对称中心的坐标；
（II）求函数f(x)的最大值，并求函数f(x)取得最大值时x的集合；
（III）求函数f(x)的增区间。
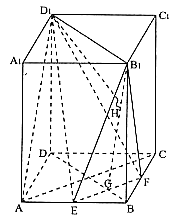
（16）（本小题共14分）
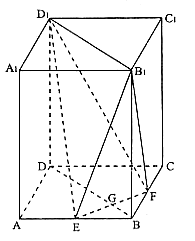
已知正四棱柱
中，底面边长为
，侧棱长为4，点E、F分别是棱AB、BC中点，EF与BD相交于G。
（I）求异面直线
和DC所成的角；
（II）求证：平面
；
（III）求点
的距离。
（17）（本小题共13分）
在盒子里有大小相同，仅颜色不同的小球共10个，其中白球5个，红球3个，黄球2个。现从中任取出一球确定颜色后再放回盒子里，最多取3次，取出黄球则不再取球。求：
（I）最多取两次就结束的概率；
（II）若取到3次，正好取到2个红球的概率；
（III）取球次数的分布列和数学期望。
（18）（本小题共14分）
已知椭圆
，过A（a，0），B（0，－b）两点的直线到原点的距离是
。
（I）求椭圆的方程；
（II）已知直线
交椭圆于不同的两点E，F，且E、F都在以B为圆心的圆上，求k的值。
（19）（本小题共12分）
已知函数
。
（I）证明：若x≠2，则有
；
（II）若数列
。
（20）（本小题共14分）
已知函数f(x)的定义域为R，对任意实数m、n都有
，且当x>0时，0<f(x)<1。
（I）证明：f(0)=1，且x<0时，f(x)>1；
（II）证明f(x)在R上单调递减；
（III）设A=
，
，若
，试确定a的取值范围。
崇文区2005－2006学年度第二学期高三统一练习（二）
数学（理工农医类）试卷参考答案及评分标准
2006.5
一、选择题
（1）A （2）A （3）C （4）B
（5）C （6）B （7）A （8）D
二、填空题
（9）
（10）－1001 （11）
（12）80 （13）
（14）正，（0，
）
三、解答题
（15）解：
（I）
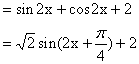
令
∴函数f(x)图象对称中心的坐标是
………………7分
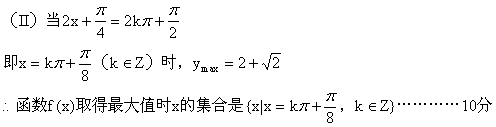
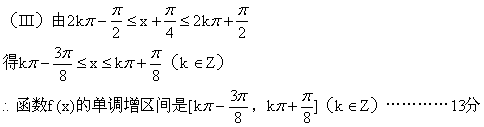
（16）解：
（I）连结
（17）解：
（I）设取球次数为
，则
（II）由题意知可以如下取球：白红红、红白红、红红白、红红黄四种情况，所以恰有两次取到红球的概率为
（III）设取球次数为
则
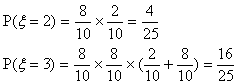
则分布列为：
|
| 1 | 2 | 3 |
| P |
|
|
|
取球次数的数学期望为
………………13分
（18）解：（I）
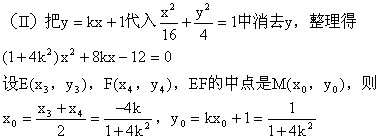
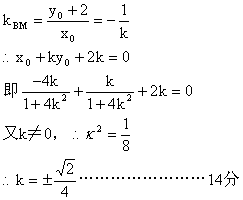
（19）证明：（I）
只需证明
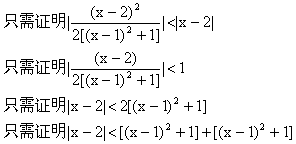
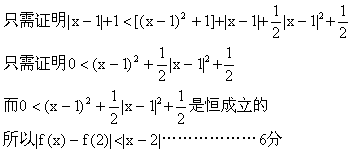
（20）（I）证明：令m=1，n=0，代入
中
得
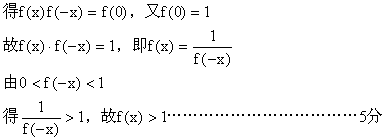
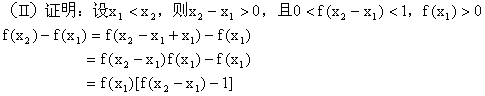
| 年级 | 高三 | 学科 | 数学 | 版本 | 期数 | ||||||||
| 内容标题 | 北京市崇文区2006年高三期末统一练习（二）数学试卷（理科） | ||||||||||||
| 分类索引号 | G.622.475 | 分类索引描述 | 统考试题与题解 | ||||||||||
| 主题词 | 北京市崇文区2006年高三期末统一练习（二）数学试卷（理科） | 栏目名称 | 高考题库 | ||||||||||
| 供稿老师 | 审稿老师 | ||||||||||||
| 录入 | 侯海静 | 一校 | 陈丽娜 | 二校 | 审核 | ||||||||