高二数学期末复习直线和圆的方程
号 班 姓名
一、选择题
1. 直线
的倾斜角
，直线
，则直线
的斜率为( )
A 
B 
C 
D 
2. 直线经过点
，
,则直线的倾斜角( )
A 450 B 1350 C －450 D －1350
3. 一条直线经过点
，倾斜角为
，则这条直线方程为( )
A 
B 
C 
D 
4. 已知直线
与
轴的交点
，与
轴的交点
，其中
，
则直线的方程为( )
A 
B 
C 
D 
5.直线的方程
的斜率和它在轴与轴上的截距分别为( )
A 
B 
C 
D 
6. 经过点
且与直线
平行的直线方程为( )
A 
B 
C 
D 
7. 过点
，且与直线
垂直的直线的方程为( )
A 
B 
C 
D 
8. 直线
：
，
：
的夹角为( )
A 
B 
C 
D 
9若实数x、y满足等式 
，那么
的最大值为( )
A.
Ｂ.
Ｃ.
Ｄ.
10.已知半径为1的动圆与圆(x－5)2+(y+7)2=16相切，则动圆圆心的轨迹方程是( )
A．(x－5)2+(y+7)2=25 B．(x－5)2+(y+7)2=17或(x－5)2+(y+7)2=15
C．(x－5)2+(y+7)2=9 D．(x－5)2+(y+7)2=25或(x－5)2+(y+7)2=9
11.已知圆x2+y2=r2在曲线x+y=4的内部，则半径r的范围是（ ）
A.0<r<2
B.0<r<
C.0<r<2
D.0<r<4
12.由曲线y=x与x2+y2=4所围成的图形的最小面积是( )
A.
B.π C.
D.
二、填空题
13. 经过原点且经过
，
交点的直线方程为
．
14. 平行线
和 
的距离为
15.无论m取何实数时，直线(m-1)x-(m+3)y-(m-11)=0恒过定点，则定点的坐标为
16满足不等式组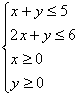
的点中，使目标函数
取得最大值的点的坐标是_____
三、解答题
17．过点
作直线，分别交轴、轴的正半轴于点
，若
的面积
最小，试求直线的方程。
18．过
两点作两条平行线，求满足下列条件的两条直线方程：
（1）两平行线间的距离为
；
（2）这两条直线各自绕
、
旋转，使它们之间的距离取最大值。
19.已知圆x2+y2+8x-4y=0与以原点为圆心的某圆关于直线y=kx+b对称，
（1）求k、b的值；（2）若这时两圆的交点为A、B，求∠AOB的度数.
20.若动圆C与圆(x-2)2+y2=1外切，且和直线x+1=0相切.求动圆圆心C的轨迹E的方程.
21.已知圆C：x2+y2－2x+4y－4=0,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点.若存在，求出直线l的方程;若不存在，说明理由.
22.设圆满足(1)y轴截圆所得弦长为2.(2)被x轴分成两段弧，其弧长之比为3∶1，在满足(1)、(2)的所有圆中，求圆心到直线l:x－2y=0的距离最小的圆的方程．
高二数学期末复习直线和圆的方程
一选择题
A，B，C，D，A，B，C，D，D， D，A，B
二、填空题
13 
14 
15 
16 (0，5)
三、解答题
17．解：设直线的方程为
，
令
，得
，故
，
令
，得
，故
，
由题意知，
，所以
，
∴的面积
，
∵ ，∴
，从而
，
当且仅当
，即
（
舍去）时，
，
所以，直线的方程为
，即
.
18．解：（1）当两直线的斜率不存在时，方程分别为
，满足题意，
当两直线的斜率存在时，设方程分别为
与
，
即：
与
，由题意：
，解得
，
所以，所求的直线方程分别为：
， 
综上：所求的直线方程分别为：，或．
（2）由（1）当两直线的斜率存在时，
，∴
，
∴
，
∴
，即
，
∴
，∴
，∴
，当
，
．
当两直线的斜率不存在时，
， ∴，
此时两直线的方程分别为
，
．
19.解：（1）圆x2+y2+8x-4y=0可写成(x+4)2+(y-2)2=20.
∵圆x2+y2+8x-4y=0与以原点为圆心的某圆关于直线y=kx+b对称，
∴y=kx+b为以两圆圆心为端点的线段的垂直平分线.∴
×k=-1，k=2.
点（0，0）与（-4，2）的中点为（-2，1），∴1=2×(-2)+b，b=5.∴k=2，b=5.
（2）圆心（-4，2）到2x-y+5=0的距离为d=
.
而圆的半径为2
，∴∠AOB=120°.
20.若动圆C与圆(x-2)2+y2=1外切，且和直线x+1=0相切.求动圆圆心C的轨迹E的方程.
解：设动圆的圆心C的坐标为（x，y），则x-(-1)+1=
，即x+2=，整理得y2=8x.所以所求轨迹E的方程为y2=8x.
21解：假设存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点.设l的方程为y=x+b,A(x1,y1),B(x2,y2).
由OA⊥OB知，kOA·kOB=－1,即
=－1,∴y1y2=－x1x2.
由
,得2x2+2(b+1)x+b2+4b－4=0,
∴x1+x2=－(b+1),x1·x2=
+2b－2,y1y2=(x1+b)(x2+b)=x1x2+b(x1+x2)+b2
=
+2b－2－b(b+1)+b2=
+b－2
∵y1y2=－x1x2 ∴
+b－2=－(+2b－2) 即b2+3b－4=0.∴b=－4或b=1.
又Δ=4(b+1)2－8(b2+4b－4)=－4b2－24b+36=－4(b2+6b－9)
当b=－4时，Δ=－4×(16－24－9)>0; =1时，Δ=－4×(1+6－9)>0
故存在这样的直线l,它的方程是y=x－4或y=x+1,即x－y－4=0或x－y+1=0.
22.解:设圆的圆心为P(a,b),半径为r，则P到x轴，y轴的距离分别为｜b｜、｜a｜，由题设知圆P截x轴所得劣弧所对圆心角为90°,故圆P截x轴所得弦长为
r=2b.
∴r2=2b2 ①又由y轴截圆得弦长为2，∴r2=a2+1 ②
由①、②知2b2－a2=1.又圆心到l:x－2y=0的距离d=
,∴5d2=(a－2b)2=a2+4b2－4ab≥a2+4b2－2(a2+b2)=2b2－a2=1.当且仅当a=b时“=”号成立，
∴当a=b时，d最小为
，由
得
或
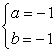由①得r=.
∴(x－1)2+(y－1)2=2或(x+1)2+(y+1)2=2为所求．