高三第二次月考数学试题
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.函数f (x) = sin x+cos x 的最小正周期是
A. B. C.π D.2π
2.在等差数列{an}中, a7=9, a13=-2, 则a25= ( )
A -22 B -24 C 60 D 64
3.若![]() 的终边所在象限是
的终边所在象限是
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.在等比数列{an}中,a3=3,S3=9,则a1= ( )
A.12 B.3 C.-6或12 D.3或12
 5.若函数
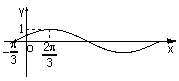
5.若函数![]() 的图象(部分)如图所示,则
的图象(部分)如图所示,则![]() 的取值是
的取值是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.已知![]() 为非零的平面向量. 甲:
为非零的平面向量. 甲:![]() 甲是乙的( )
甲是乙的( )
A.充分条件但不是必要条件 B.必要条件但不是充分条件
C.充要条件 D.非充分条件非必要条件
7.已知O是△ABC内一点,且满足·=·=·,则O点一定是△ABC的
A.内心 B.外心 C.垂心 D.重心
8.函数![]() 为增函数的区间是
为增函数的区间是
A.
![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9.为了得到函数![]() 的图象,可以将函数
的图象,可以将函数![]() 的图象
的图象
A.向右平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向左平移个单位长度
10.设![]() 是某港口水的深度y(米)关于时间t(时)的函数,其中
是某港口水的深度y(米)关于时间t(时)的函数,其中![]() .下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
经长期观察,函数![]() 的图象可以近似地看成函数
的图象可以近似地看成函数![]() 的图象.下面的函数中,最能近似表示表中数据间对应关系的函数是(
的图象.下面的函数中,最能近似表示表中数据间对应关系的函数是(![]() )( )
)( )
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
11.在四边形ABCD中,![]() 其中
其中![]() 不共线,则四边形ABCD是
不共线,则四边形ABCD是
A.梯形 B.矩形 C.菱形 D.正方形
12.已知-9,a1,a2,-1四个实数成等差数列,-9,b1,b2,b3,-1五个实数成等比数列,则b2(a2-a1)=
A.8 B.-8 C.±8 D.
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在横线上.
13.设α为第四象限的角,若,则tan2α =_____________.
14.已知![]() ,
,![]() ,
,![]() ∥
∥![]() ,则t=
.
,则t=
.
15.已知向量![]() ,且A,B,C三点共线,则k=
.
,且A,B,C三点共线,则k=
.
16.若数列![]() 为等差数列,则数列
为等差数列,则数列![]() 也为等差数列,类比上述性质,相应地,若数列{cn}是等比数列且
也为等差数列,类比上述性质,相应地,若数列{cn}是等比数列且![]() ,则有数列dn=
(n∈N+)也是等比数列.
,则有数列dn=
(n∈N+)也是等比数列.
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17.(本题满分12分)化简f(x)=cos(π+2x)+cos(π-2x)+2(x∈R,k∈Z),并求函数f(x)的值域和最小正周期.
18.(本小题满分12分)
已知等差数列{an}的首项a1=1,公差d>0,且第二项,第五项,第十四项分别是等比数列{bn}的第二项,第三项,第四项.
⑴求数列{an}与{bn}的通项公式.
⑵设数列{cn}对任意正整数n,均有![]() ,求c1+c2+c3+…+c2005的值.
,求c1+c2+c3+…+c2005的值.
19.(本题满分12分)A、B、C为△ABC的三内角,且其对边分别为a、b、c.若![]() =(-cos,sin),
=(-cos,sin),![]() =(cos,sin),且
=(cos,sin),且![]() ·
·![]() =.
=.
(1)求A;(2)若a=2,三角形面积S=,求b+c的值.
20.(本题满分12分)已知![]() .
.
⑴求证:![]() 互相垂直;
互相垂直;
⑵若![]() 大小相等,求
大小相等,求![]() (其中k为非零实数).
(其中k为非零实数).
21.(本小题满分12分)
正数数列{an}的前n项和为Sn,且2.
(1) 试求数列{an}的通项公式;
(2)设bn=,{bn}的前n项和为Tn,求证:Tn<.
22.(本题满分14分)设关于x的函数![]() 的最小值为
的最小值为![]() .
.
⑴
写出![]() 的表达式;
的表达式;
⑵试确定能使![]() 的
的![]() 值,并求出此时函数
值,并求出此时函数![]() 的最大值.
的最大值.
高三第二次月考数学试题参考答案
一、选择题(每小题5分,共60分):
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | D | D | C | B | C | C | B | A | A | B |
二、填空题(每小题4分,共16分)
(13) ![]() (14)
(14) ![]() (15)
(15) ![]() (16)
(16) ![]()
三、解答题(共74分,按步骤得分)
17.解:![]()
![]()
![]()
所以函数f(x)的值域为![]() ,最小正周期
,最小正周期![]() 。
。
18.⑴由题意得(a1+d)(a1+13d)=(a1+4d)2(d>0) 解得d=2,∴an=2n-1,bn=3n-1.
⑵当n=1时,c1=3 当n≥2时,∵![]() ∴
∴![]() 故
故![]()
![]()
19.解:(1)∵![]() =(-cos,sin),
=(-cos,sin),![]() =(cos,sin),且
=(cos,sin),且![]() ·
·![]() =,
=,
∴-cos2+sin2=,………………………………………………2分
即-cosA=,又A∈(0,π),∴A=π………………………………5分
(2)S△ABC=bc·sinA=b·c·sin π=![]() ,∴bc=4 …………………7分
,∴bc=4 …………………7分
又由余弦定理得:a2=b2+c2-2bc·cos120°=b2+c2+bc ………………10分
∴16=(b+c)2,故b+c=4.……………………………………………12分
19.解:⑴由![]()
得![]() ,
,![]()
又![]()
![]()
![]()
(2)![]()
![]() 同理
同理![]()
由![]() 得
得![]()
又![]() 所以
所以![]() 因
因![]() 所以
所以![]()
20.(1)∵an>0,![]() ,∴
,∴![]() ,则当n≥2时,
,则当n≥2时,
![]() 即
即![]() ,而an>0,∴
,而an>0,∴![]()
又![]()
(2)![]()
22.(1)f(x)=1-2a-2acosx-2sin2x=1-2a-2acosx-2(1-cos2x)=2(cosx-)2--2a-1。
当a≥2时,则cosx=1时,f(x)取最小值,即f(a)=1-4a;
当-2<a<2时,则cosx=时,f(x)取最小值,即f(a)=--2a-1;
当a≤-2时,则cosx=-1时,f(x)取最小值,即f(a)=1;
综合上述,有f(a)=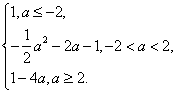
(2)若f(a)=,a只能在[-2,2]内。
解方程--2a-1=,得a=-1,和a=-3。因-1∈[-2,2],故a=-1为所求,此时
f(x)=2(cosx+)2+;当cosx=1时,f(x)有最大值5。