吉林省延边二中2005~2006学年度第一学期
高三年级数学学科基础训练(十五)时间:
(命题范围:三角函数)
一. 单项选择题(在每题给出的四个选项中,只有一项是最符合题目要求的。每题5分,共60分)
1.若A、B、C是△ABC的三个内角,且A<B<C(C≠![]() ),则下列结论中正确的是( )
),则下列结论中正确的是( )
A.sinA<sinC B.cotA<cotC C.tanA<tanC D.cosA<cosC
2.若角α满足条件sin2![]() <0,cos
<0,cos![]() -sin
-sin![]() <0,则
<0,则![]() 在( )
在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.在△ABC中,若2cosBsinA=sinC,则△ABC的形状一定是( )
A.等腰直角三角形 B.直角三角形
C.等腰三角形 D.等边三角形
4.已知f(x)是定义在(0,3)上的函数,f(x)的图象如图1所示,那么不等式f(x)cosx<0的解集是( )
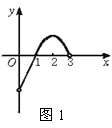 A.(0,1)∪(2,3) B.(1,
A.(0,1)∪(2,3) B.(1,![]() )∪(
)∪(![]() ,3)
,3)
C.(0,1)∪(![]() ,3) D.(0,1)∪(1,3)
,3) D.(0,1)∪(1,3)
5.若![]() =1,则
=1,则![]() 的值为( )
的值为( )
A.3 B.-3 C.-2 D.-![]()
6.若![]() ,且sin
,且sin![]() =
=![]() (
(![]() ),则
),则![]() = (
)
= (
)
A. ![]() B.
B.
![]() 或
或 ![]() C.
C. ![]() D.
D.
![]()
7.已知下列四个命题正确的个数为 ( )
(1)若点P(a,2a)(a![]() 0)为角
0)为角![]() 终边上的一点,则sin
终边上的一点,则sin![]() =
=![]() ;
;
(2)若![]() 且都是第一象限角,则
且都是第一象限角,则![]() ;
;
(3)若![]() 是第二象限角,则
是第二象限角,则![]() >0;
>0;
(4)若sinx+cosx=![]() ,则
,则![]() .
.
A. 1 B. 2 C. 3 D.4
8.在△ABC中,已知cosA=![]() ,sinB=
,sinB=![]() ,则cosC=
( )
,则cosC=
( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D.
D. ![]()
9. ![]() 等于 ( )
等于 ( )
A. cos![]() B.
cot2
B.
cot2![]() C. tan
C. tan![]() D.tan2
D.tan2![]()
10. ![]() 等于 ( )
等于 ( )
A. cot![]() B. cot2
B. cot2![]() C.
tan
C.
tan![]() D. tan2
D. tan2![]()
11.tan15![]() +cot15
+cot15![]() 等于(
)
等于(
)
A. 2
B. ![]() C. 1 D.
C. 1 D. ![]()
12. 设![]() ,且sin
,且sin![]() +
+![]() =sin
=sin![]() ,
, ![]() 则
则![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或 ![]() D.
D. ![]()
二 填空题(每题5分,共20分)
13.若函数y=2sinx+![]() cosx+4的最小值为1,则a = _____ .
cosx+4的最小值为1,则a = _____ .
14. ![]() 的值为_____________.
的值为_____________.
15. 在△ABC中,已知A、B、C成等差数列,则![]() =______.
=______.
16. 设a为第四象限的角,若 ![]() ,则tan 2a =______________.
,则tan 2a =______________.
答题卡
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
13_________________14_________________15_________________16_________________
三 解答题(共5题,每题14分)
17. 已知![]() 为第二象限的角,
为第二象限的角,![]() ,
,![]() 为第一象限的角,
为第一象限的角,![]() .求
.求![]() 的值.
的值.
18. 已知![]() =2,求 (I)
=2,求 (I)![]() 的值; (II)
的值; (II)![]() 的值.
的值.
19. 已知函数![]() 求使
求使![]() 为正值的
为正值的![]() 的集合.
的集合.
20. 已知向量![]() ,
,
求![]() 的值.
的值.
21.是否存在角![]() 、
、![]() ,
,![]()
![]() ,
,![]() ,使等式sin(3
,使等式sin(3![]() -
-![]() )=
)=![]() cos
cos![]() ,
,
![]()
![]() 同时成立,若存在,求出
同时成立,若存在,求出![]() 、
、![]() 的值。若不存在,说明理由。
的值。若不存在,说明理由。
1.答案:D
解析一:因为A<C.在△ABC中,大角对大边.因此c>a,即2RsinC>2RsinA.所以sinC>sinA.
解析二:利用特殊情形.因为A、B、C为△ABC的三个内角.因此,存在C为钝角的可能,而A必为锐角.此时结论仍然正确.而cosA、tanA、cotA均为正数,cosC、tanC、cotC均为负数.因此B、C、D均可排除.
解析三:作差sinA-sinC=2cos![]() ·sin
·sin![]() ,A、B、C为△ABC的三个内角,又A<C.因此0<A+C<π,0<
,A、B、C为△ABC的三个内角,又A<C.因此0<A+C<π,0<![]() <
<![]() ,-π<A-C<0,-
,-π<A-C<0,-![]() <
<![]() <0.所以cos
<0.所以cos![]() >0,sin
>0,sin![]() <0,可得sinA<sinC.
<0,可得sinA<sinC.
评述:本题入口较宽,做为考查三角函数的基本题,有一定的深刻性,尤其是被选项的设计隐藏着有益的提示作用.为观察、思考能力强的考生提供了快速解题的可能性.本题在考查基础知识的同时,考查了逻辑思维能力及灵活运用知识解题的能力.
 2.答案:B
2.答案:B
解析:sin2α=2sinαcosα<0 ∴sinαcosα<0
即sinα与cosα异号,∴α在二、四象限,
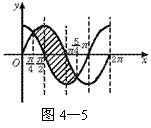
又cosα-sinα<0
∴cosα<sinα
由图4—5,满足题意的角α应在第二象限
3.答案:C
解析:2sinAcosB=sin(A+B)+sin(A-B)又∵2sinAcosB=sinC,
∴sin(A-B)=0,∴A=B
4.答案:C
解析:解不等式f(x)cosx<0
∴ ∴0<x<1或
∴0<x<1或![]() <x<3
<x<3
5.答案:A
解析:由![]() =1,解得:tanθ=-
=1,解得:tanθ=-![]()
∴ ,
,
∴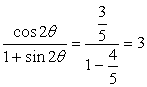
6. C 7. A 8.A 9.B 10.B 11 .C 12 .D
13.答案:5 解析:y=![]() sin(x+
sin(x+![]() )+4在x∈R时,ymin=4-
)+4在x∈R时,ymin=4-![]()
而4-![]() =1解得a=5.
=1解得a=5.
14.答案:2-![]()
![]()
![]() .
.
15. 解:因为A、B、C成等差数列,又A+B+C=180°,所以A+C=120°
从而![]() =60°,故tan
=60°,故tan![]() .由两角和的正切公式,
.由两角和的正切公式,
得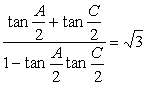 .所以
.所以![]()
![]() .
.
16. ![]()
17. ![]()
18. 解:(I)∵ tan![]() =2, ∴
=2, ∴ 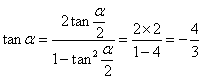 ;
;
所以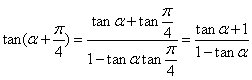 =
=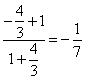 ;
;
(II)由(I), tanα=-![]() , 所以
, 所以![]() =
=![]() =
=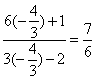 .
.
19.解:∵![]() ………………………………………………2分
………………………………………………2分
![]() …………………………………………………4分
…………………………………………………4分
![]()
![]() …………6分
…………6分
![]() …………………………8分
…………………………8分
![]() …………………………………………10分
…………………………………………10分
又![]() ∴
∴![]() ………………………12分
………………………12分
20. 解法一:
![]()
![]()
![]()
![]()
![]()
由已知![]() ,得
,得![]()
又![]()
所以![]()
![]()
![]()
解法二:
![]()
![]()
![]()
由已知![]() ,得
,得![]()
![]()
![]()