第二章 函数
2.1 映射与函数、函数的解析式
一、选择题:
1.设集合![]() ,
,![]() ,则下述对应法则
,则下述对应法则![]() 中,不能构成A到B的映射的是( )
中,不能构成A到B的映射的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.若函数![]() 的定义域为[-1,2],则函数
的定义域为[-1,2],则函数![]() 的定义域是( )
的定义域是( )
A.![]() B.[-1,2] C.[-1,5] D.
B.[-1,2] C.[-1,5] D.![]()
3,设函数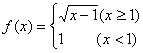 ,则
,则![]() =( )
=( )
A.0 B.1 C.2 D.![]()
4.下面各组函数中为相同函数的是( )
A.![]() B.
B.![]()
C.![]() D.
D.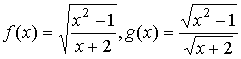
5. 已知映射![]() :
:![]() ,其中,集合
,其中,集合![]() 集合B中的元素都是A中元素在映射
集合B中的元素都是A中元素在映射![]() 下的象,且对任意的
下的象,且对任意的![]() 在B 中和它对应的元素是
在B 中和它对应的元素是![]() ,则集合B中元素的个数是( )
,则集合B中元素的个数是( )
(A) 4 (B) 5 (C) 6 (D) 7
6.有下述对应:
①集合A=R,B=Z,对应法则是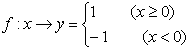 ,其中
,其中![]() ,
,![]() .
.
②集合A和B都是正整数集N*,对应法则是![]() ,
,![]() ,
,![]() .
.
③集合![]() ,对应法则是
,对应法则是![]() .
.
④集合![]() 是三角形},
是三角形},![]() ,对应法则是
,对应法则是![]() 的面积.
的面积.
则其中是集合A到集合B的映射的是 ,是集合A到集合B的一一映射的是
7.已知定义在![]() 的函数
的函数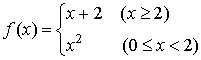
若![]() ,则实数
,则实数![]()
8.已知![]() 是二次函数,且满足
是二次函数,且满足![]() .
.
9.已知![]() 是常数,
是常数,![]() ),且
),且![]() (常数),
(常数),
(1)求![]() 的值; (2)若
的值; (2)若![]() 、b的值.
、b的值.
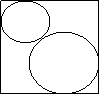 10.如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为x,两圆的面积之和为S,将S表示为x的函数,求函数
10.如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为x,两圆的面积之和为S,将S表示为x的函数,求函数![]() 的解析式及
的解析式及![]() 的值域.
的值域.
2.2函数的定义域和值域
1.已知函数![]() 的定义域为M,f[f(x)]的定义域为N,则M∩N=
.
的定义域为M,f[f(x)]的定义域为N,则M∩N=
.
2.如果f(x)的定义域为(0,1),![]() ,那么函数g(x)=f(x+a)+f(x-a)的定义域为
.
,那么函数g(x)=f(x+a)+f(x-a)的定义域为
.
3. 函数y=x2-2x+a在[0,3]上的最小值是4,则a= ;若最大值是4,则a= .
4.已知函数f(x)=3-4x-2x2,则下列结论不正确的是( )
A.在(-∞,+∞)内有最大值5,无最小值 B.在[-3,2]内的最大值是5,最小值是-13
C.在[1,2)内有最大值-3,最小值-13 D.在[0,+∞)内有最大值3,无最小值
5.已知函数![]() 的值域分别是集合P、Q,则( )
的值域分别是集合P、Q,则( )
A.p![]() Q B.P=Q C.P
Q B.P=Q C.P![]() Q D.以上答案都不对
Q D.以上答案都不对
6.若函数![]() 的定义域为R,则实数m的取值范围是( )
的定义域为R,则实数m的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.函数![]() 的值域是( )
的值域是( )
A.[0,2] B.[1,2] C.[-2,2] D.[-![]() ,
,![]() ]
]
8.若函数![]() 的定义域是( )
的定义域是( )
A.![]() B.
B.![]() C.
C.![]() D.[3,+∞
D.[3,+∞![]()
9.求下列函数的定义域:
①![]() ②
②![]()
③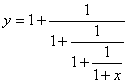
10.求下列函数的值域:
①![]() ②y=x+5+x-6 ③
②y=x+5+x-6 ③![]()
④![]() ⑤
⑤![]()
11.设函数![]() .
.
(Ⅰ)若定义域限制为[0,3],求![]() 的值域;
的值域;
(Ⅱ)若定义域限制为![]() 时,
时,![]() 的值域为
的值域为![]() ,求a的值.
,求a的值.
12.若函数![]() 的值域为[-2,2],求a的值.
的值域为[-2,2],求a的值.
2.3函数的单调性
1.下述函数中,在![]() 上为增函数的是( )
上为增函数的是( )
A.y=x2-2 B.y=![]() C.y=
C.y=![]() D.
D.![]()
2.下述函数中,单调递增区间是![]() 的是( )
的是( )
A.y=-![]() B.y=-(x-1) C.y=x2-2 D.y=-x
B.y=-(x-1) C.y=x2-2 D.y=-x
3.函数![]() 上是( )
上是( )
A.增函数 B.既不是增函数也不是减函数 C.减函数 D.既是减函数也是增函数
4.若函数f(x)是区间[a,b]上的增函数,也是区间[b,c]上的增函数,则函数f(x)在区间[a,b]上是( )
A.增函数 B.是增函数或减函数 C.是减函数 D.未必是增函数或减函数
5.已知函数f(x)=8+2x-x2,如果g(x)=f(2-x2),那么g(x) ( )
A.在区间(-1,0)上单调递减 B.在区间(0,1)上单调递减
C.在区间(-2,0)上单调递减 D在区间(0,2)上单调递减
6.设函数![]() 上是单调递增函数,那么a的取值范围是( )
上是单调递增函数,那么a的取值范围是( )
A.![]() B.
B.![]() C.a<-1或a>1 D.a>-2
C.a<-1或a>1 D.a>-2
7.函数![]() 时是增函数,则m的取值范围是( )
时是增函数,则m的取值范围是( )
A. [-8,+∞) B.[8,+∞) C.(-∞,- 8] D.(-∞,8]
8.如果函数f(x)=x2+bx+c对任意实数t都有f(4-t)=f(t),那么( )
A.f(2)<f(1)<f(4) B.f(1)<f(2)<f(4) C.f(2)<f(4)<f(1) D.f(4)<f(2)<f(1)
9.若函数![]() 的单调递减区间是
的单调递减区间是![]() ,则实数a的值为
.
,则实数a的值为
.
10.若a>0,求函数![]() 的单调区间.
的单调区间.
11.设函数![]() ,
,
(I)求证:当且仅当a≥1时,f(x)在![]() 内为单调函数;
内为单调函数;
(II)求a的取值范围,使函数f(x)在区间![]() 上是增函数.
上是增函数.
2.4 函数的奇偶性
1.若![]() 是( )
是( )
A.奇函数 B.偶函数 C.奇函数或偶函数 D.非奇非偶函数
2.设f(x)为定义域在R上的偶函数,且f(x)在![]() 的大小顺序为( )
的大小顺序为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.如果f(x)是定义在R上的偶函数,且在![]() 上是减函数,那么下述式子中正确的是( )
上是减函数,那么下述式子中正确的是( )
A.![]() B.
B.![]()
C.![]() D.以上关系均不成立
D.以上关系均不成立
4.函数f(x)、f(x+2)均为偶函数,且当x∈[0,2]时,f(x)是减函数,设![]() b= f(7.5),c= f(-5),则a、b、c的大小关系是( )
b= f(7.5),c= f(-5),则a、b、c的大小关系是( )
A.a>b>c B.a> c > b C.b>a> c D.c> a>b
5.下列4个函数中:①y=3x-1,②![]() ③
③![]() ,
,
④![]() 其中既不是奇函数,又不是偶函数的是( )
其中既不是奇函数,又不是偶函数的是( )
A.① B.②③ C.①③ D.①④
6.已知f(x)是定义在R上的偶函数,并满足:![]() ,当2≤x≤3,f(x)=x,则f(5.5)=( )
,当2≤x≤3,f(x)=x,则f(5.5)=( )
A.5.5 B.-5.5 C.-2.5 D.2.5
7.设偶函数f(x)在![]() 上为减函数,则不等式f(x)> f(2x+1)
的解集是
上为减函数,则不等式f(x)> f(2x+1)
的解集是
8.已知f(x)与g(x)的定义域都是{xx∈R,且x≠±1},若f(x)是偶函数,g(x)是奇函 数,且f(x)+ g(x)=![]() ,则f(x)=
,g(x)=
.
,则f(x)=
,g(x)=
.
9.已知定义域为(-∞,0)∪(0,+∞)的函数f(x)是偶函数,并且在(-∞,0)上是增函数,若f(-3)=0,则不等式![]() <0的解集是
.
<0的解集是
.
10.设定义在R上的偶函数f(x)又是周期为4的周期函数,且当x∈[-2,0]时f(x)为增函数,若f(-2)≥0,求证:当x∈[4,6]时, f(x)为减函数.
11.设f(x)是定义在R上的偶函数,在区间(-∞,0)上单调递增,
且满足f(-a2+2a-5)<f(2a2+a+1), 求实数a的取值范围.
2.5 反函数
1、下列函数中,有反函数的是( )
A.y =3
+![]() B.y =
B.y =![]()
C.y =![]() D.y=
D.y= 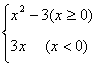
2、设点(a,b)在函数y=f(x)的图象上,那么y= f-1(x)的图象上一定有点( )
A.(a, f -1(a) ) B.(f -1(b),b) C.( f -1(a),a) D.(b, f -1(b))
3、若f(x-1)= x2-2x+3 (x≤1),则f-1(4)等于( )
A.![]() B.1-
B.1-![]() C.-
C.-![]() D.
D.![]() -2
-2
4、与函数y=f(x)的反函数图象关于原点对称的图象所对应的函数是( )
A.y=-f(x) B.y= f -1(x) C.y =-f -1(x) D.y =-f -1(-x)
5、函数f(x)=![]() +2 (x≥1)的反函数是( )
+2 (x≥1)的反函数是( )
A.y= (x-2)2+1 (x∈R) B.x= (y-2)2+1 (x∈R)
C.y= (x-2)2+1 (x≥2) D.y=(x-2)2+1 (x≥1)
6.函数![]() 有反函数
有反函数![]() ,将
,将![]() 的图象绕原点顺时针方向旋转90°后得到另一个函数的图象,则得到的这个函数是( )
的图象绕原点顺时针方向旋转90°后得到另一个函数的图象,则得到的这个函数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.若点(4,3)既在函数![]() 的图象上,又在它的反函数的图象上,则函数的解析式
的图象上,又在它的反函数的图象上,则函数的解析式
8、 若函数f(x)存在反函数f-1(x),则f-1(f(x))=____ ; f(f-1(x))=______.
9.关于反函数给出下述命题:
①
若![]() 为奇函数,则
为奇函数,则![]() 一定有反函数.
一定有反函数.
②
函数![]() 有反函数的充要条件是
有反函数的充要条件是![]() 是单调函数.
是单调函数.
③
若![]() 的反函数是
的反函数是![]() ,则函数
,则函数![]() 一定有反函数,且它的反函数是
一定有反函数,且它的反函数是![]()
④
设函数![]() 的反函数为
的反函数为![]() ,若点P(a,b)在
,若点P(a,b)在![]() 的图象上,则点
的图象上,则点![]() 一定在
一定在![]() 的图象上.
的图象上.
⑤若两个函数的图象关于直线![]() 对称,则这两个函数一定互为反函数.
对称,则这两个函数一定互为反函数.
则其中错误的命题是
10、己知f(x)=![]() (x≥1)
(x≥1)
①求f(x)的反函数f -1(x),并求出反函数的定义域; ②判断并证明f -1(x)的单调性.
11.已知函数![]() 存在反函数
存在反函数![]() ,
,
(1)若![]() 是奇函数,讨论
是奇函数,讨论![]() 的奇偶性;
的奇偶性;
(2)若![]() 在定义域上是增函数,讨论
在定义域上是增函数,讨论![]() 的单调性.
的单调性.
2.6 .指数式与对数式
1.若![]() N*,则
N*,则![]() ( )
( )
A.2 B.![]() C.
C.![]() D.
D.![]()
2.若![]() ,则
,则![]() ( )
( )
A.4 B.16 C.256 D.81
3. 已知2lg(x-2y)=lgx+lgy,则![]() 的值为( )
的值为( )
A.1 B.4 C.1或4 D.4 或-1
4.已知![]() ,
,![]()
![]() ,
,![]()
![]() ,则
,则![]() 的值分别为( )
的值分别为( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
5.设![]() ,则
,则![]() 与
与![]() 的大小关系为( )
的大小关系为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]() 与
与![]() 的大小关系不确定
的大小关系不确定
6.计算:![]()
![]() _____________
_____________
7.计算:![]() =
.
=
.
8.已知![]() ,
,![]() ,则
,则![]() 用 a, b
表示为
.
用 a, b
表示为
.
9.计算![]() .
.
10.已知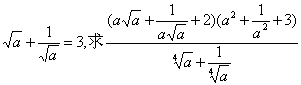 的值.
的值.
2.7 .指数函数与对数函数
1.当![]() 时,
时,![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.已知![]() ,其中
,其中![]() ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.函数![]() 的定义域为[1,2],则函数
的定义域为[1,2],则函数![]() 的定义域为( )
的定义域为( )
A.[0,1] B.[1,2] C.[2,4] D.[4,16]
4.若函数![]() 上单调递减,则实数a的取值范围是( )
上单调递减,则实数a的取值范围是( )
A.[9,12] B.[4,12] C.[4,27] D.[9,27]
5.若![]() ≥
≥![]() ,则( )
,则( )
A.![]() ≥0 B.
≥0 B.![]() ≥0 C.
≥0 C.![]() ≤0 D.
≤0 D.![]() ≤0
≤0
6.若定义在(—1,0)内的函数![]() 满足
满足![]() >0,则a的取值范围是
>0,则a的取值范围是
7.若![]() ,则实数k的取值范围是
.
,则实数k的取值范围是
.
8.已知函数![]() 的值域为R,则实数a的取值范围是
.
的值域为R,则实数a的取值范围是
.
9.已知函数![]() ,
,
(1)求![]() 的定义域;
的定义域;
(2)此函数的图象上是否存在两点,过这两点的直线平行于x轴?
(3)当a、b满足什么条件时![]() 恰在
恰在![]() 取正值.
取正值.
10.求函数![]() 的值域.
的值域.
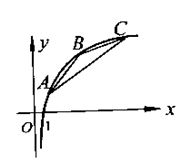 11.在函数
11.在函数![]() 的图象上有A、B、C三点,它们的横坐标分别为
的图象上有A、B、C三点,它们的横坐标分别为![]() 、
、![]() 、
、![]() ,若△ABC的面积为S,求函数
,若△ABC的面积为S,求函数![]() 的值域.
的值域.
12.已知函数![]()
(1)讨论![]() 的奇偶性与单调性;
的奇偶性与单调性;
(2)若不等式![]() 的解集为
的解集为![]() 的值;
的值;
(3)求![]() 的反函数
的反函数![]() ;
;
(4)若![]() ,解关于
,解关于![]() 的不等式
的不等式![]() R).
R).
2.8 .二次函数
1.设函数![]() R)的最小值为m(a),当m(a)有最大值时a的值为( )
R)的最小值为m(a),当m(a)有最大值时a的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知![]() (k为实数)的两个实数根,则
(k为实数)的两个实数根,则![]() 的最大值为( )
的最大值为( )
A.19 B.18 C.![]() D.不存在
D.不存在
3.设函数![]() ,对任意实数t都有
,对任意实数t都有![]() 成立,则函数值
成立,则函数值![]() 中,最小的一个不可能是( )
中,最小的一个不可能是( )
A.f(-1) B.f(1) C.f(2) D.f(5)
4.设二次函数f(x),对x∈R有![]() =25,其图象与x轴交于两点,且这两点的横坐标的立方和为19,则f(x)的解析式为
=25,其图象与x轴交于两点,且这两点的横坐标的立方和为19,则f(x)的解析式为
5.已知二次函数![]() 在区间[-3,2]上的最大值为4,则a的值为
在区间[-3,2]上的最大值为4,则a的值为
6.一元二次方程![]() 的一根比1大,另一根比-1小,则实数a的取值范围是
的一根比1大,另一根比-1小,则实数a的取值范围是
7.已知二次函数![]() R)满足
R)满足![]() 且对任意实数x都有
且对任意实数x都有![]() 的解析式.
的解析式.
8.a>0,当![]() 时,函数
时,函数![]() 的最小值是-1,最大值是1.
求使函数取得最大值和最小值时相应的x的值.
的最小值是-1,最大值是1.
求使函数取得最大值和最小值时相应的x的值.
9.已知![]() 在区间[0,1]上的最大值是-5,求a的值.
在区间[0,1]上的最大值是-5,求a的值.
10.函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() ,
,
(Ⅰ)求x<0时![]() 的解析式;
的解析式;
(Ⅱ)问是否存在这样的正数a,b,当![]() 的值域为
的值域为![]() ?若存在,
?若存在,
求出所有的a,b的值;若不存在,说明理由.
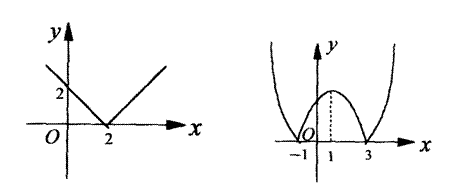
11.某蔬菜基地种植西红柿,由历年市场行情得知,从2月1日起的300天内,西红柿市场售价与上市时间的关系用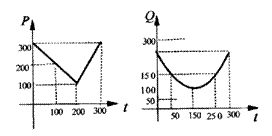 左图的一条折线表示;西红柿的种植成本与上市时间的关系用右图的抛物线段表示。
左图的一条折线表示;西红柿的种植成本与上市时间的关系用右图的抛物线段表示。
(Ⅰ)写出左图表示的市场售价与时间的函数关系P=f(t);写出右图表示的种植成本与时间的函数关系式Q=g(t);
(Ⅱ)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大.
(注:市场售价和种植成本的单位:元/102kg,时间单位:天)
2.9 .函数的图象
1.函数![]() 的图象,可由
的图象,可由![]() 的图象经过下述变换得到( )
的图象经过下述变换得到( )
 A.向左平移6个单位
A.向左平移6个单位
B.向右平移6个单位
C.向左平移3个单位
D.向右平移3个单位
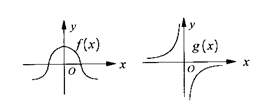
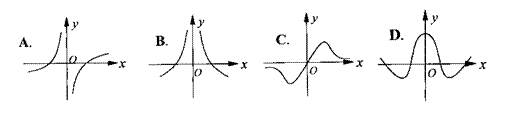
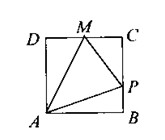
2.设函数![]() 与函数
与函数![]() 的图象如右图所示,则函数
的图象如右图所示,则函数![]() 的图象可能是下面的( )
的图象可能是下面的( )
 |
 3.已知
3.已知![]() 函数
函数![]() 的图象与函数与
的图象与函数与![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
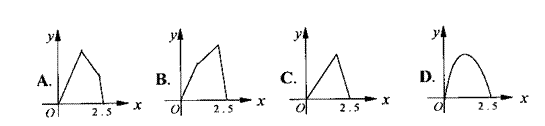 4.如图,点P在边长的1的正方形的边上运动,设M是CD边的中点,当P沿A→B→C→M运动时,以点P经过的路程
4.如图,点P在边长的1的正方形的边上运动,设M是CD边的中点,当P沿A→B→C→M运动时,以点P经过的路程![]() 为自变量,
为自变量,![]() 的面积为
的面积为![]() ,则函数
,则函数![]() 的图象大致是( )
的图象大致是( )
5.已知函数![]() 给出下列四个命题:①函数的图象关于点(1,1)对称; ②函数的图象关于直线
给出下列四个命题:①函数的图象关于点(1,1)对称; ②函数的图象关于直线![]() 对称; ③函数在定义域内单调递减;④将函数图象向左平移一个单位,再向下平移一个单位后与函数
对称; ③函数在定义域内单调递减;④将函数图象向左平移一个单位,再向下平移一个单位后与函数![]() 重合. 则其中正确命题的序号是
重合. 则其中正确命题的序号是
6.设函数![]() 的定义域为R,则下列命题中:
的定义域为R,则下列命题中:
①若![]() 为偶函数,则
为偶函数,则![]() 的图象关于
的图象关于![]() 轴对称;
轴对称;
②若![]() 为偶函数,则
为偶函数,则![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
③若![]() ,则
,则![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
④函数![]() 与函数
与函数![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
则其中正确命题的序号是
7.作出下述函数图象:
(1)![]() (2)
(2)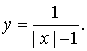 (3)
(3)![]()
8.指出函数![]() 与
与![]() 、
、![]() 为常数)的对称性,并证明你的结论.
为常数)的对称性,并证明你的结论.
9.设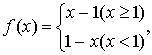 作出下述函数的图象:
作出下述函数的图象:
(1)![]() ; (2)
; (2)![]()
10.![]() 为何值时,直线
为何值时,直线![]() 与曲线
与曲线![]() 有两个公共点?有一个公共点?无公共点?
有两个公共点?有一个公共点?无公共点?
11.设函数![]() 的图象为
的图象为![]() 、
、![]() 关于点A(2,1)的对称的图象为
关于点A(2,1)的对称的图象为![]() ,
,![]() 对应的函数为
对应的函数为![]() , (Ⅰ)求函数
, (Ⅰ)求函数![]() 的解析式,并确定其定义域;
的解析式,并确定其定义域;
(Ⅱ)若直线![]() 与
与![]() 只有一个交点,求
只有一个交点,求![]() 的值,并求出交点的坐标.
的值,并求出交点的坐标.
2.10 函数的综合应用
1.某商品零售价2002年比2000年上涨了25%,欲控制2003年比2000年只上涨10%,则2003年应比2002年降价( )
A.15% B.12% C.10% D.5%
2.某物体一天中的温度T是时间t的函数![]() ,时间单位是小时,温度单位为摄氏度,t=0表示中午12:00,其后t取值为正,则下午3时的温度为( )摄氏度.
,时间单位是小时,温度单位为摄氏度,t=0表示中午12:00,其后t取值为正,则下午3时的温度为( )摄氏度.
A.8 B.18 C.78 D.112
3.从1999年11月1日起,全国储蓄存款征收利息税,利息税的税率为20%,即储蓄利息的20%由各银行储蓄点代收,某人在1999年11月存入人民币1万元,存期一年,年利率为2.25%,则到期可净得到的本金和利息共计( )
A.10225元 B.10180元 C.11800元 D.12250元
4.水箱中有水20m3,如果打开出水孔,水箱中的水5分钟可以流完,当打开出水孔时,水箱中的水的剩余量![]() 是时间t(秒)的函数,则函数
是时间t(秒)的函数,则函数![]() 的解析式是
的解析式是
5.按国家统计局资料,到1989年初,我国大陆人口总数达到11亿,人口自然增长率约为14%,按此自然增长率计算,我国大陆人口达到13亿时是 年初(填写年号),(用下面数据帮助计算:lg13=1.1139,lg11=1.0414,lg1.14=0.0060)
 三、解答题:
三、解答题:
6.(理科)A、B两镇相距50公里,A镇位于一直线形河岸旁,B镇离河岸的距离BD=30公里. 两镇准备在河岸C处合建一个水厂,从水厂C到A、B两镇的水管费用每公里分别为500元和1000元,问水厂C应建在何处才能使水管总费用最省,并求出最小水管总费用.
7.有两个煤矿用汽车供应三个城镇的用煤,第一个煤矿月产煤120万吨,第二个煤矿月产煤200万吨. 第一个城镇每月用煤90万吨,第二个城镇每月用煤150万吨,第三个城镇每月用煤80万吨,又知第一个煤矿与三城镇的中心供应站的距离分别为20公里、10公里和12公里;第二个煤矿与三个城城镇的中心站的距离分别为8公里、16公里和30公里,问怎样调配煤才能使总的运输费用最少?
8.某工厂生产一种机器的固定成本为5000元,且每生产100台需要增加投入2500元,对销售市场进行调查后得知,市场对此产品的需求量为每年500台,已知销售收入函数为:![]() 其中x是产品售出的数量,且
其中x是产品售出的数量,且![]() .(I)若x为年产量,y为利润,求
.(I)若x为年产量,y为利润,求![]() 的解析式;(II)当年产量为何值时,工厂的年利润最大,其最大值是多少?
的解析式;(II)当年产量为何值时,工厂的年利润最大,其最大值是多少?
9.我国是水资源比较贫乏的国家之一,各地采用价格调控等手段来达到节约用水的目的. 某市用水收费的方法是:水费=基本费+超额费+损耗费. 若每月用水量不超过最低限量![]() 时,只付基本费8元和每户的定额损耗费c元;若用水量超过
时,只付基本费8元和每户的定额损耗费c元;若用水量超过![]() 时,除了付同上的基本费和损耗费外,超过部分每1m3付b元的超额费. 已知每户每月的定额损耗费c不超过5元. 该市某家庭今年一月份、二月份和三月份的用水量和支付的费用如下表所示:
时,除了付同上的基本费和损耗费外,超过部分每1m3付b元的超额费. 已知每户每月的定额损耗费c不超过5元. 该市某家庭今年一月份、二月份和三月份的用水量和支付的费用如下表所示:
| 月 份 | 用水量 | 水 费 |
| 一月份 | 9 | 9元 |
| 二月份 | 15 | 19元 |
| 三月份 | 22 | 33元 |
根据表格中的数据,求a、b、c.
10.轮船由甲地逆水匀速行驶至乙地,甲、乙两地相距![]() ,水流速度为常数
,水流速度为常数![]() ,船在静水中的最大速度为
,船在静水中的最大速度为![]() ,已知轮船每小时的燃料费用与船在静水中的速度
,已知轮船每小时的燃料费用与船在静水中的速度![]() 的平方成正比,比例系数为常数k. (I)将全程燃料费用y(元)表示为静水中速度
的平方成正比,比例系数为常数k. (I)将全程燃料费用y(元)表示为静水中速度![]() 的函数;(II)为了使全程的燃料费用最小,船的实际前进速度应为多少?
的函数;(II)为了使全程的燃料费用最小,船的实际前进速度应为多少?
第二章 函数单元测试卷
一、选择题:共12个小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.函数y=![]() (x≥1)的反函数是( )
(x≥1)的反函数是( )
A、y=![]() B、y=
B、y=![]()
![]() C、y=
C、y=![]() (x>0) D、y=
(x>0) D、y=![]()
2.函数![]() ,
,![]() [0,3]的值域是( )
[0,3]的值域是( )
A、![]() B、[-1,3] C、[0,3] D、[-1,0]
B、[-1,3] C、[0,3] D、[-1,0]
3.某种细菌在培养过程中,每20分钟分裂一次(一个分裂为两个),经过3小时这种细菌由1个可繁殖成 ( )
A、511个 B、512个 C、1023个 D、1024个
4.拟定从甲地到乙地通话m分钟的电话费由f(m)=1.06(0.50×[m]+1)给出,其中m>0,[m]是大于或等于m的最小整数(例如[3]=3,[3.7]=4, [3.1]=4),则从甲地到乙地通话时间为5.5分钟的话费为 ( )
A.3.71 B.3.97 C.4.24 D.4.77
5.已知![]() ,那么
,那么![]() 用
用![]() 表示是( )
表示是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.设0<![]() <1,实数
<1,实数![]() 满足
满足![]() ,则y关于x的函数的图像大致形状是( )
,则y关于x的函数的图像大致形状是( )
|
A B C D
7.不等式![]() 的解集是( )
的解集是( )
A.(0,1) B.(![]() 1,1) C.
1,1) C.![]() D.
D.![]()
8.关于![]() 的不等式
的不等式![]() 的解为( )
的解为( )
A.0<![]() <2 B.0<
<2 B.0<![]() <1 C.
<1 C.![]() <2 D.
<2 D.![]() >1
>1
9.如果函数![]() 对任意实数
对任意实数![]() ,都有
,都有![]() ,则( )
,则( )
A、![]() <
<![]() <
<![]() B、
B、![]() <
<![]() <
<![]()
C、![]() <
<![]() <
<![]() D、
D、![]() <
<![]() <
<![]()
10.已知![]() 的反函数
的反函数![]() 的图像的对称中心是(-1,3),则实数a等于( )
的图像的对称中心是(-1,3),则实数a等于( )
A.2 B.3 C.-2 D.-4
11.集合![]() ,映射
,映射![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() 是奇数,则这样的映射共有( )
是奇数,则这样的映射共有( )
A.60个 B.45个 C.27个 D.11个
12.已知定义在实数R上的函数![]() 不恒为零,同时满足
不恒为零,同时满足![]() 且当x>0时,f(x)>1,那么当x<0时,一定有( )
且当x>0时,f(x)>1,那么当x<0时,一定有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本题共4小题,每小题4分,满分16分,请把答案填在题中横线上.
13.若![]() 为函数
为函数![]() 的反函数,则
的反函数,则![]() 的值域是
.
的值域是
.
14.函数![]() 恒成立,则b的最小值是
.
恒成立,则b的最小值是
.
15.老师给出一个函数y=f(x),四个学生甲、乙、丙、丁各指出这个函数的一个性质:
甲:对于x∈R,都有f(1+x)=f(1-x); 乙:在![]() 上函数递减;
上函数递减;
丙:在(0,+∞)上函数递增; 丁:f(0)不是函数的最小值。
如果其中恰有三人说得正确,请写出一个这样的函数 .
16.关于函数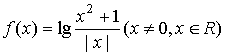 ,有下列命题:
,有下列命题:
①
函数y=![]() 的图像关于y轴对称; ② 当x>0时
的图像关于y轴对称; ② 当x>0时![]() 是增函数,当x<0时
是增函数,当x<0时![]() 是减函数;
是减函数;
③
函数![]() 的最小值是lg2; ④
当x>1,时
的最小值是lg2; ④
当x>1,时![]() 没有反函数。
没有反函数。
其中正确命题的序号是 (注:把你认为正确的序号都填上).
三、解答题:本题共6小题,满分74分,解答应写出文字说明、证明过程或演算步骤.
17.(满分12分)某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.02元. 根据市场调查,销售商一次订购量不会超过500件.
(Ⅰ) 设一次订购量为![]() 件,服装的实际出厂单价为P元,写出函数
件,服装的实际出厂单价为P元,写出函数![]() 的表达式;
的表达式;
(Ⅱ) 当销售商一次订购了450件服装时,该服装厂获得的利润是多少元?
(服装厂售出一件服装的利润=实际出厂单价-成本)
18.(满分12分)设定义在![]() 上的函数
上的函数![]() 满足下面三个条件:
满足下面三个条件:
(1)对于任意正实数a、b,都有![]() ,其中p是正的实常数;
,其中p是正的实常数;
(2)![]() ; (3)当
; (3)当![]() 时,总有
时,总有![]() .
.
(Ⅰ)求![]() 的值(写成关于p的表达式);(Ⅱ)求证:
的值(写成关于p的表达式);(Ⅱ)求证:![]() 上是减函数.
上是减函数.
19.(满分12分)某工厂有216名工人接受了生产1000台GH型高科技产品的总任务,已知每台GH型产品由4个G型装置和3个H型装置配套组成. 每个工人每小时能加工6个G型装置或3个H型装置. 现将工人分成两组同时开始加工,每组分别加工一种装置。设加工G型装置的工人有![]() 人,他们加工完G型装置所需时间为
人,他们加工完G型装置所需时间为![]() ,其余工人加工完H型装置所需时间为
,其余工人加工完H型装置所需时间为![]() (单位:小时,可以不是整数). (Ⅰ)写出
(单位:小时,可以不是整数). (Ⅰ)写出![]() 解析式;(Ⅱ)比较
解析式;(Ⅱ)比较![]() 与
与![]() 的大小,并写出这216名工人完成总任务的时间
的大小,并写出这216名工人完成总任务的时间![]() 的解析式;(Ⅲ)应怎样分组,才能使完成总任务用的时间最少?
的解析式;(Ⅲ)应怎样分组,才能使完成总任务用的时间最少?
20.(满分12分)设函数![]()
![]()
![]()
![]() 为奇函数,又
为奇函数,又![]() ,且
,且![]() 在
在![]() 上递增。 ⑴求
上递增。 ⑴求![]() 、
、![]() 、
、![]() 的值; ⑵当
的值; ⑵当![]() 时,讨论
时,讨论![]() 的单调性.
的单调性.
21.(满分12分)已知f(x)是定义在[-1,1]上的奇函数。 当a, b∈[-1,1],
且a+b≠0时,有![]() 成立。(Ⅰ)判断函f(x)的的单调性,并证明;
成立。(Ⅰ)判断函f(x)的的单调性,并证明;
(Ⅱ)若f(1)=1,且f(x)≤m2-2bm+1对所有x∈[-1,1],b∈[-1,1]恒成立,求实数m的取值范围。
22.(满分14分) 已知二次函数![]() 中
中![]() 均为实数,且满足
均为实数,且满足
![]() ,对于任意实数x都有
,对于任意实数x都有![]() ,并且当
,并且当![]() 时有
时有
![]() 成立。(Ⅰ)求f(1)的值; (Ⅱ)证明:
成立。(Ⅰ)求f(1)的值; (Ⅱ)证明:![]() ; (Ⅲ)当x∈[-2,2]且a+c取最小值时,函数
; (Ⅲ)当x∈[-2,2]且a+c取最小值时,函数![]() (m为实数)是单调函数,求证:
(m为实数)是单调函数,求证:![]() .
.
第二章 函数参考答案或解答过程
2.1 映射与函数、函数的解析式
1.D(提示:作出各选择支中的函数图象). 2.C(提示:由![]() ). 3.B(提示:由内到外求出).4.D(提示:考察每组中两个函数的对应法则与定义域).5.A 6.①、③、④;③.(提示:对照“映射”、“一一映射”的定义). 7.
). 3.B(提示:由内到外求出).4.D(提示:考察每组中两个函数的对应法则与定义域).5.A 6.①、③、④;③.(提示:对照“映射”、“一一映射”的定义). 7.![]() (提示:由外到里,逐步求得k).
(提示:由外到里,逐步求得k).
8.设![]() ,
, ![]() +c
+c
![]()
![]() , 这是一个恒等式
, 这是一个恒等式
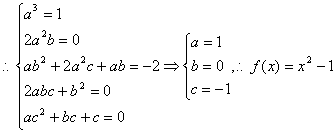 .
.
9.(1)![]() ,
,
![]()
上式是关于x的恒等式,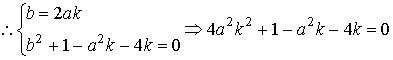
![]() ,
,
若![]() ,
,
(2)![]()
而![]() ,代入上式得
,代入上式得![]() ,
,
解得![]() ,不合,
,不合,![]() .
.
10.设另一个圆的半径为y,则![]()
![]()
![]() ,
, ![]()
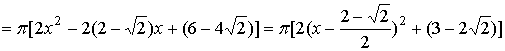 ,
,
∵当一个圆为正方形内切圆时半径最大,而另一圆半径最小,∴函数的定义域为![]() (注意定义域为闭区间)
(注意定义域为闭区间) ![]()
![]() ,∴函数
,∴函数![]() 的值域为
的值域为![]() .
.
2.2函数的定义域和值域
1.![]() 2.
2.![]() 3.5;1 4.C 5.C 6. D
3.5;1 4.C 5.C 6. D
7.A(提示:![]() ,然后推得). 8. B
,然后推得). 8. B
9.①![]() ②
②![]() ③
③ ![]()
10.①![]() ②
②![]() ③
③![]() ④
④![]() ⑤
⑤![]()
11.![]() ,∴对称轴为
,∴对称轴为![]() ,
,
(Ⅰ)![]() ,∴
,∴![]() 的值域为
的值域为![]() ,即
,即![]() ;
;
(Ⅱ)![]() 对称轴
对称轴![]() ,
,
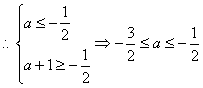 , ∵区间
, ∵区间![]() 的中点为
的中点为![]() ,
,
(1)当![]() 时,
时,![]() ,
,
![]() 不合);
不合);
(2)当![]() 时,
时,![]() ,
,
![]() 不合);
不合);
综上,![]() .
.
12.![]() 的判别式恒小于零,∴函数的定义域为R,∴原函数等价于
的判别式恒小于零,∴函数的定义域为R,∴原函数等价于![]() ,
,
即![]() 的解集为[-2,2](其中包含y=1),
的解集为[-2,2](其中包含y=1),
![]() 是方程
是方程![]() 的根,
的根,
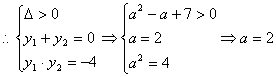 .
.
2.3函数的单调性
1.C 2.D 3.B 4.A
5.A 6.B 7.C 8.A 9.3 10.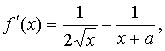
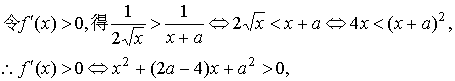
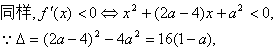
(1)当a.>1时,对x∈(0,+∞)恒有![]() >0, ∴当a.>1时,f(x)在(0,+∞)上为增函数;
>0, ∴当a.>1时,f(x)在(0,+∞)上为增函数;
(2)当a=1时,f(x)在(0,1)及(1,+∞)都是增函数,且f(x)在x=1处连续,∴f(x)在(0,+∞)内为增函数;
(3)当0<a<1时,△>0,解方程x2+(2a-4)x+a2=0
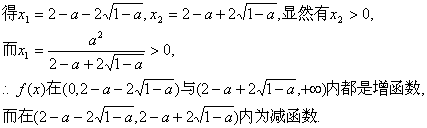
11.(I)![]() ,
,
①当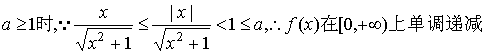
②当0<a<1时,由f′(x)<0,得![]()
由f′(x)>0得![]()
∴当0<a<1时,f(x)在![]() ,为增函数,
,为增函数,
∴当0<a<1时,f(x)在 ![]() 上不是单调函数;
上不是单调函数;
(另证)令f(x) =1![]()
当0<a<1时,f(x)在 ![]() 上存在两点x1=0 或
上存在两点x1=0 或![]() ,使f(x1)= f(x2)=1,故f(x)不是单调函数.
,使f(x1)= f(x2)=1,故f(x)不是单调函数.
综上,当且反当a≥1时,f(x)在![]() 上为单调函数.
上为单调函数.
(II)由(I)①知当a≥1时f(x)单调递减,不合; 由②知当f(x)在![]() 上单调递增等价于:
上单调递增等价于:![]()
![]() ,即a的取值范围是
,即a的取值范围是![]()
2.4 函数的奇偶性
1.A 2.A
3.A
4.A 5.C 6.D 7.x<-1或x>-![]() ; 8.
; 8.![]() ; 9.(-3,0)∪(3,+∞)
; 9.(-3,0)∪(3,+∞)
10.[证明] 这是“抽象”函数问题,应熟练运用奇偶性、周期性、单调性的定义证明.
在[4,6]内任取x1、x2,设4≤x1<x2≤6,

12.∵![]() 为R上的偶函数,
为R上的偶函数,
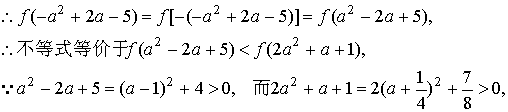
∵![]() 在区间
在区间![]() 上单调递增,而偶函数图象关于y轴对称, ∴
上单调递增,而偶函数图象关于y轴对称, ∴![]() 在区间(0,+∞)上单调递减,
在区间(0,+∞)上单调递减,
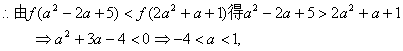
∴实数a的取值范围是(-4,1).
2.5 反函数
1.B 2.D
3.C 4.D 5.C 6.B(提示:作一个示意图,如令![]() ).7.
).7.![]() (提示:将(4,3)与(3,4)分别代入原函数解析式,不必求出反函数). 8. x ,x 9.①、②(提示:奇函数不一定是单调函数;例如
(提示:将(4,3)与(3,4)分别代入原函数解析式,不必求出反函数). 8. x ,x 9.①、②(提示:奇函数不一定是单调函数;例如![]() 它不是单调函数(∵它有两个单调区间),但它是一一对应的,有反函数,∴②错).
它不是单调函数(∵它有两个单调区间),但它是一一对应的,有反函数,∴②错).
10①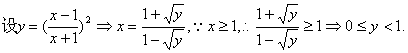
即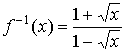 ,f-1(x)的定义域为
,f-1(x)的定义域为![]()
②设![]()
所以f-1(x)在![]() 上单调递增.
上单调递增.
11.证明:(1)![]()
![]() 是奇函数,定义域关于原点对称,
是奇函数,定义域关于原点对称,![]() 的值域也关于原点对称。
的值域也关于原点对称。![]() 的定义域关于原点对称,设
的定义域关于原点对称,设![]() ,存在
,存在![]() 使
使![]() ,则
,则![]() ,
,
![]()
![]() 是奇函数,
是奇函数,![]() ,
,![]() ,
,![]() ,
,
所以![]() 也是奇函数.
也是奇函数.
(2)设![]() ,且
,且![]() ,存在
,存在![]() ,使
,使![]() ,
,![]() ,由于
,由于![]() 在定义域上是增函数,所以
在定义域上是增函数,所以![]() ,即
,即![]() ,
,![]() 在定义域上也是单调增函数.
在定义域上也是单调增函数.
2.6 .幂、指数式与对数式
1.A 2.C 3.B 4.D 5.B 6.12
7.解:原式![]()
![]()
![]()
8.解:∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() , ∴
, ∴![]()
9.10 10.![]() ,
,
![]() ,
,
![]()
![]() ,
,
而![]() ,
,
![]() .
.
2.7 .指数函数与对数函数
1.B 2.C 3.D 4.A
5.B 6.![]() 7.
7.![]() 8.
8.![]()
9.(1)![]() ,
,
又![]() ,故函数的定义域是
,故函数的定义域是![]() .
.
(2)问题的结论取决于![]() 的单调性,考察这个函数的单调性有三种方法:
的单调性,考察这个函数的单调性有三种方法:
①求导,②运用单调性定义,③复合分析,但以方法①最好.
(解一)求导得:![]()
![]() ,
,
![]() ,
,![]() ,
,
![]() 在定义域内单调递增,故不存在所述两点;
在定义域内单调递增,故不存在所述两点;
(解二)任取![]() ,则
,则![]() ,
,
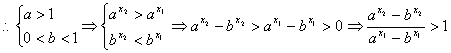 ,
,
![]() 即
即![]() 在定义域内单调递增,故不存在所述两点;
在定义域内单调递增,故不存在所述两点;
(3)![]() 在
在![]() 单调递增,∴命题等价于:
单调递增,∴命题等价于:![]() ,
,![]()
10.![]()
![]() ,
,
(1)当![]() ,即
,即![]() 时,
时,![]() ;
;
(2)当![]() ,即
,即![]() 时,
时,![]() 上单调递减,
上单调递减,
![]() ,
,![]() 值域为
值域为![]() .
.
11.设A、B、C在![]() 轴上的射影分别为A1、B1、C1,
轴上的射影分别为A1、B1、C1,
![]()
![]()
![]() ,
,
令![]() ,
,
![]() ,
,
![]() 的值域为
的值域为![]()
12.(1)![]() 定义域为
定义域为![]() 为奇函数;
为奇函数;
![]() ,求导得
,求导得![]() ,
,
①当![]() 时,
时,![]() 在定义域内为增函数;
在定义域内为增函数;
②当![]() 时,
时,![]() 在定义域内为减函数;
在定义域内为减函数;
(2)①当![]() 时,∵
时,∵![]() 在定义域内为增函数且为奇函数,
在定义域内为增函数且为奇函数,
![]() ;
;
②当![]() 在定义域内为减函数且为奇函数,
在定义域内为减函数且为奇函数,
![]() ;
;
(3)![]()
![]() R);
R);
(4)![]() ,
,
![]() ;①当
;①当![]() 时,不等式解集为
时,不等式解集为![]() R;
R;
②当![]() 时,得
时,得![]() ,不等式的解集为
,不等式的解集为![]() ;
;
③当![]()
2.8 .二次函数
1.C 2.B
3.B 4.![]() ; 5.-3或
; 5.-3或![]() ; 6.-2<a<0;
; 6.-2<a<0;
7.由![]() ∵对
∵对![]() R,
R,
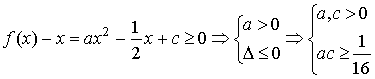
而![]() ,∴
,∴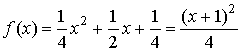
8.∵a>0,∴f(x)对称轴![]()
①当![]()
②当![]() ∴
∴![]() .
.
综上,当![]()
9.∵f(x)的对称轴为![]() ①当
①当![]()
②当![]()
③当![]() 不合;
不合;
综上,![]()
10.(Ⅰ)当![]() (Ⅱ)∵当
(Ⅱ)∵当![]() 若存在这样的正数a,b,则当
若存在这样的正数a,b,则当![]() ∴f(x)在[a,b]内单调递减,
∴f(x)在[a,b]内单调递减,
∴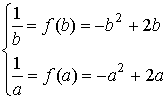
![]() 是方程
是方程![]() 的两正根,
的两正根,
![]()
11.(Ⅰ)![]() 将(50,150)代入得
将(50,150)代入得![]()
所以![]()
(Ⅱ)设时刻t的纯收益为![]()
①当![]()
∴当t=50时![]()
②当200![]()
∴当t=300时取最大值87.5<100;故第50天时上市最好.
2.9 .函数的图象
1.D.(提示:变换顺序是![]() .
.
2.A.(提示:![]() 为奇函数,且
为奇函数,且![]() 时无定义,故只有A).3.A.(提示:设
时无定义,故只有A).3.A.(提示:设![]() 4.A.(提示:分三段分析 ).
4.A.(提示:分三段分析 ).
5.①、②、④.(提示:![]() 只有③错,∵它有两个单调区间). 6.②、④.
只有③错,∵它有两个单调区间). 6.②、④.
7.(1) (2) (3)
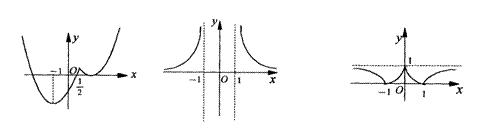 |
8.
设P关于直线![]() 对称的点
对称的点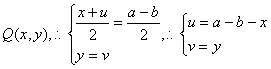 代入①得
代入①得
![]() 即
即![]() ,
,![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称.
对称.
 9.(1)
(2)
9.(1)
(2)
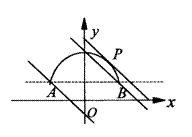 10.作出
10.作出![]() 的图象(如图半圆)与
的图象(如图半圆)与![]() 的图象(如图平行的直线,将
的图象(如图平行的直线,将![]() 代入
代入![]() 得
得![]() ,将
,将![]() 代入
代入![]() 得
得![]() ,当
,当![]() 与半圆相切于P时可求得
与半圆相切于P时可求得![]()
则①当![]() 时,
时,![]() 与曲线有两个公共点;
与曲线有两个公共点;
②当![]() 或
或![]() 时,有一个公共点;
时,有一个公共点;
③当![]() 或
或![]() 时,无公共点;
时,无公共点;
11.(Ⅰ)设![]() 是
是![]() 上任意一点,
上任意一点,![]() ① 设P关于A(2,1)对称的点为
① 设P关于A(2,1)对称的点为![]() 代入①得
代入①得![]()
![]()
(Ⅱ)联立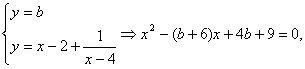
![]() 或
或![]()
(1)当![]() 时得交点(3,0); (2)当
时得交点(3,0); (2)当![]() 时得交点(5,4).
时得交点(5,4).
2.10 函数的综合应用
1.B 2.C 3.B 4.![]() 5.2001年
5.2001年
6.![]()
![]() ,则水管总费用
,则水管总费用
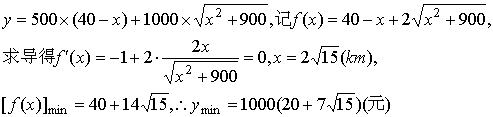
7.设第一个煤矿供应三个城镇的用煤量分别为x、y、z万吨,∴第二个煤矿供应三个城镇的用煤量分别为![]() 万吨,又设每万吨煤运输1公里的费用为1,
万吨,又设每万吨煤运输1公里的费用为1,
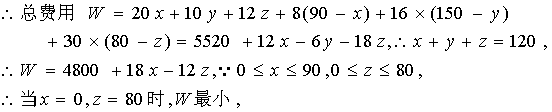
故,第一个煤矿供应三个城镇的用煤量分别为0万吨、40万吨、80万吨,第二个煤矿供应三个镇的用煤量分别为90万吨、110万吨、0万吨时总运输费用最小.
8.(I)![]() ,产品全部售出;当
,产品全部售出;当![]() 时,产品只能售出500台,
时,产品只能售出500台,
故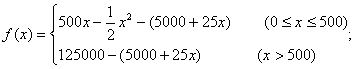
(II)当![]()
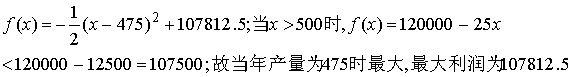
9.设每月水量为![]() ,支付水费为y元;
,支付水费为y元;
则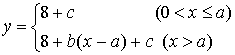 ,
,![]()
将x=15,x=22分别代入②得b=2, 2a=c+19③,假设一月份用水量超过最低限量,即
![]() 代入②得
代入②得![]() 与③矛盾,
与③矛盾,![]()
代入③得![]()
10.(I)∵船在全程行驶的时间![]()
(II)![]()
当![]()
①当![]() 时,函数唯一的极小点在定义域
时,函数唯一的极小点在定义域![]() 内,
内,![]() 取最小值,此时轮船的实际前进速度为
取最小值,此时轮船的实际前进速度为![]()
②当![]() 时,函数在定义域内单调递减,
时,函数在定义域内单调递减,![]() 取最小值,此时轮船的实际前进速度为
取最小值,此时轮船的实际前进速度为![]()
函数单元测试参考答案
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | B | B | C | A | A | D | B | A | A | B | D |
二、填空题:13、![]() ; 14、
; 14、![]() ; 15、
; 15、![]() 等; 16、①③
等; 16、①③
三、解答题:
17.解:(Ⅰ)当![]() 时,P=60;当
时,P=60;当![]() 时,P=60-0.02(
时,P=60-0.02(![]()
所以 
(Ⅱ)设销售商的一次订购是![]() 件时,工厂获得的利润为L元,则
件时,工厂获得的利润为L元,则
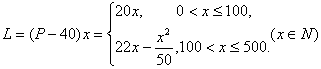
当![]() 时,L=5850. 因此,当销售商一次订购了450件服装时,该厂获得的利润是5850元.
时,L=5850. 因此,当销售商一次订购了450件服装时,该厂获得的利润是5850元.
18.解:(1)取a=b=1,则![]() ……2分
……2分
又![]() . 且
. 且![]() .
.
得:![]() ……5分
……5分
(2)设![]() 则:
则:![]()
![]()
![]() ………8分 依
………8分 依![]()
再依据当![]() 时,总有
时,总有![]() 成立,可得
成立,可得![]() ………10分
………10分
即![]() 成立,故
成立,故![]() 上是减函数。………12分
上是减函数。………12分
19.解:(Ⅰ)由题意知,需加工G型装置4000个,加工H型装置3000个,所用工人分别为![]() 人,
人,![]() 人.
人. ![]()
即![]() ……3分
……3分
(Ⅱ)![]() ……4分
……4分 ![]()
当![]() ;
;
当![]() ……6分
……6分
![]()
 ……8分
……8分
(Ⅲ)完成总任务所用时间最少即求![]() 的最小值.
的最小值.
当![]() 时,
时,![]() 递减,
递减,![]()
![]() 此时
此时![]() 当
当![]() 时,
时,![]() 递增,……10分
递增,……10分
![]()
![]() 此时
此时![]()
![]() ∴加工G型装置,H型装置的人数分别为86,130或87,129。
∴加工G型装置,H型装置的人数分别为86,130或87,129。
20.解:⑴∵![]() 为奇函数,∴
为奇函数,∴![]() ,
,

∴![]() =0或
=0或![]() =1。而
=1。而![]() =0时
=0时![]() =
=![]() ,
,![]() 矛盾 ∴
矛盾 ∴![]() =1,
=1,![]() =1,
=1,![]() =0
=0
⑵由⑴![]()
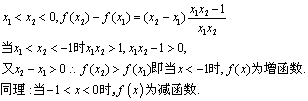
注意:第(2)小题理科同学可用导数来处理。
21、(Ⅰ)证明:设![]() ∈[—1,1],且
∈[—1,1],且![]() ,在
,在![]() 中,令a=x1,b=—x2, 有
中,令a=x1,b=—x2, 有![]() >0,∵x1<x2,∴x1-x2<0 又∵f(x)是奇数,∴f(-x2)=-f(x2)∴
>0,∵x1<x2,∴x1-x2<0 又∵f(x)是奇数,∴f(-x2)=-f(x2)∴![]() >0 ∴f(x1)-f(x2)<0,即f(x1)< f(x2).
>0 ∴f(x1)-f(x2)<0,即f(x1)< f(x2).
故f(x)在[-1,1]上为增函数……6分
(Ⅱ)解:∵f(1)=1 且f(x )在[-1,1]上为增函数,对x∈[-1,1],有f(x)≤f(1)=1。
由题意,对所有的x∈[-1,1],b∈[—1,1],有f(x)≤m2-2bm+1恒成立,
应有m2-2bm+1≥1![]() m2-2bm≥0。
记g(b)=-2mb+m2,对所有的b∈[-1,1],g(b)≥0成立.
m2-2bm≥0。
记g(b)=-2mb+m2,对所有的b∈[-1,1],g(b)≥0成立.
只需g(b)在[-1,1]上的最小值不小于零……8分
若m>0时,g(b)=-2mb+m2是减函数,故在 [-1,1]上,b=1时有最小值,
且[g(b)]最小值=g(1)=-2m+m2≥0![]() m≥2;
m≥2;
若m=0时,g(b)=0,这时[g(b)]最小值=0满足题设,故m=0适合题意;
若m<0时,g(b)=-2mb+m2是增函数,故在[-1,1]上,b=-1时有最小值,
且[g(b)]最小值=g(-1)=2m+m2≥0![]() m≤-2.
m≤-2.
综上可知,符合条件的m的取值范围是:m∈(-![]() ,-2
,-2![]() ∪{0}∪[2,+
∪{0}∪[2,+![]()
![]() 。
。
22.解:(Ⅰ)∵对于任意x∈R,都有f(x)—x≥0,且当x∈(0,2)时,
有f(x)≤(![]() )2·令x=1 ∴1≤f(1)≤(
)2·令x=1 ∴1≤f(1)≤(![]() )2.即f(1)=1.……4分
)2.即f(1)=1.……4分
(Ⅱ)由a—b+c=0及f(1)=1.
有![]() 可得b=a+c=
可得b=a+c=![]() .……6分
.……6分
又对任意x,f(x)—x≥ 0,即ax2—![]() x+c≥0. ∴a>0且△≤0.
x+c≥0. ∴a>0且△≤0.
即![]() —4ac≤0。解得ac≥
—4ac≤0。解得ac≥![]() .……9分
.……9分
(Ⅲ)由(Ⅱ)可知a>0,c>0. a+c≥2![]() ≥2·
≥2·![]() =
=![]() .……10分
.……10分
![]() a=c,
a=c,
当且仅当
a+c=![]() 时等号成立。此时a=c=
时等号成立。此时a=c=![]() ……11分
……11分
∴f(x)=![]() x2+
x2+![]() x+
x+![]() , F(x)=f(x)-mx=
, F(x)=f(x)-mx=![]() [x2+(2-4m)x+1]……12分
[x2+(2-4m)x+1]……12分
当x∈[-2,2]时,F(x)是单调的,所以F(x)的顶点一定在[-2,2]的外边.
∴![]() ≥2 解得m≤-
≥2 解得m≤-![]() 或m≥
或m≥![]() ……14分
……14分
