第四章 三角函数
§4-1 任意角的三角函数
一、选择题：
1．使得函数
有意义的角在（ ）
（Ａ）第一，四象限 （Ｂ）第一，三象限 （Ｃ）第一、二象限 （Ｄ）第二、四象限
２．角α、β的终边关于У轴对称，（κ∈Ζ）。则
（Ａ）α＋β＝２κπ （Ｂ）α－β＝２κπ
（Ｃ）α＋β＝２κπ－π （Ｄ）α－β＝２κπ－π
３．设θ为第三象限的角，则必有（ ）
（Ａ）
（Ｂ）
（Ｃ）
（Ｄ）
４．若
，则θ只可能是（ ）
（Ａ）第一象限角 （Ｂ）第二象限角 （C）第三象限角 （Ｄ）第四象限角
５．若
且
，则θ的终边在（ ）
(A)第一象限 （B）第二象限 （C）第三象限 （D）第四象限
二、填空题：
6．已知α是第二象限角且
则2α是第▁▁▁▁象限角，
是第▁▁▁象限角。
7．已知锐角α终边上一点A的坐标为（2sina3,-2cos3）,则α角弧度数为▁▁▁▁。
8．设
则Y的取值范围是▁▁▁▁▁▁▁。
9．已知cosx-sinx<-1，则x是第▁▁▁象限角。
三、解答题：
10．已知角α的终边在直线
上，求sinα及cot
的值。
11．已知Cos(α+β)+1=0, 求证：sin(2α+β)+sinβ=0。
12．已知
，求ƒ（1）+ƒ（2）+ƒ（3）+……+ƒ（2000）的值。
§4-2 同角三角函数的基本关系式及诱导公式
一、选择题：
1．
化简结果是（ ）
（A）0 （B）
（C）2
2．若
，且
，则
的值为（ ）
或
3.
已知
，且
，则
的值为（ ）
4.
已知，并且
是第一象限角，则的值是（ ）
5.
化简
的结果是（ ）
6.
若
且
，则角所在的象限是（ ）
（A）一、二象限 （B）二、三象限 （C）一、三象限 （D）一、四象限
填空题：
7．化简
▁▁▁▁▁▁。
8．已知
，则
的值为▁▁▁▁▁▁。
9．
=▁▁▁▁▁。
10．若关于
的方程
的两根是直角三角形两锐角的正弦值，则
▁▁▁▁。
解答题：
11．已知：
，求
的值。
12．已知
，求证：
13．已知
，且
，求
的值。
14．若
化简：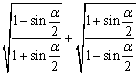
§4-3：两角和与差的三角函数
1“
”是“
”的（ ）
(A)充分必要条件 （B）必要不充分条件
（C）充要条件 （D）既不充分也不必要条件
2 已知
且
为锐角，则
为（ ）
或
非以上答案
3
设
则下列各式正确的是（ ）
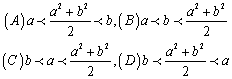
4
已知
，且
则
的值是（ ）
二、填空题：
5
已知
则
的值为
6
已知
且
则
7
已知
则
8
在
中，
是方程
的两根，则
三、解答题：
9
求值
。
10 求证：
11
中，BC=5，BC边上的高AD把面积分为
，又是方程
的两根，求
的度数。
§4-4 二倍角的正弦、余弦、正切
一．选择题：
1． 
的值为（
）
2． 已知
, 则
的值为（
）
3． 已知
, 则
的值为（
）
4． 函数
的定义域是（
）
5． 中，
， 
则
的大小为（
）
或
或
二．填空题：
6． 已知
，若
，则
若
, 则
7． 若
, 则
8． 若
,则
的值为_______
9． 
已知
,则
三．解答题：
10 求值
11 化简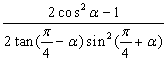
12．设
均为锐角，且
，求
的最大值。
§4-5 三角函数的化简和求值
一．选择题：
1． 在中，若
，则的形状是（ ）
等腰三角形 
直角三角形 
等边三角形 等腰直角三角形
2． 设
，
，则
的值为（ ）
3． 
的值为（ ）
4． 若
，则
的值为（ ）
5． 已知
，
，则
的值为（ ）
二．填空题：
6． 函数
的最小正周期
7． 一个等腰三角形一个底角的正弦值为
，则这个三角形顶点的正切为
8． 若
，则
9．
三．解答题：
10．已知是第二，三象限的角，化简：
11．已知
且
，求
和
的值
12．求值：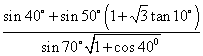
13．已知
，
，
，求
的值。
§4-6 三角函数的恒等变形
1． 求值：
2 求证：
3 求证：
4 试探讨
，
，成立的充要条件（A，B所满足的关系）。
5
已知三个内角A.B.C成等差数列，且
，求
的值（参考公式：
）
6 已知，
为锐角，且
，
，求证
。
§4-7 三角函数的图象
一．选择题：
１．要得到
的图象，只要将函数
的图象（ ）
向左平移
单位
向右平移单位
向左平移
单位 向右平移单位
２．以下给出的函数中，以
为周期的偶函数是（ ）
３．函数
在同一区间内的
处取最大值
，在
处取得最小值
，则函数解析式为（ ）
4．
的图象是（ ）
 |  | ||||
 | |||||
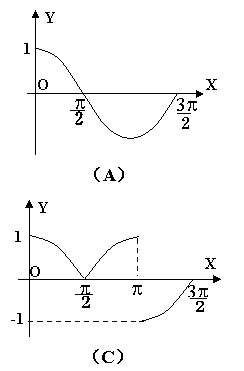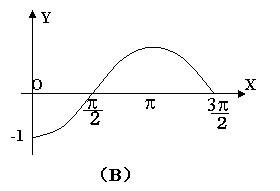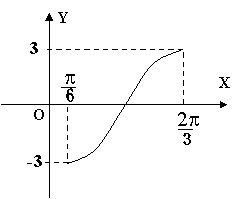5. 三角函数式
①
② 
③
④
其中在
上的图象如图所示的函数是（ ）
③ ①
② ①
② ④ ①
② ③ ④
二．填空题：
6．把函数
的图象向左平移
个单位，所得图象关于y轴对称，则
的最小值是
7。若函数具有以下性质：
⑴关于y轴对称 ⑵对于任意
，都有
则
的解析式
为
（只须写出满足条件的的一个解析式即可）
8．若
，且
，求角的取值范围
9．已知
且的周期不大于1，则最小正常数
三．解答题：
10．已知函数
（1）求函数的最小正周期
（2）求函数的增区间
（3）函数的图象可由函数
的图象经过怎样的变换得出？
（１） 若把函数的图象向左平移
单位得一偶函数，求的最小值
１１．已知函数
（１） 求的定义域
（２） 求函数的单调增区间
（３） 证明直线
是图象的一条对称轴
１２．设
，周期为，且有最大值
（１） 试把化成
的形式，并说明图象可由
的图象经过怎样的平移变换和伸缩变换得到
（２） 若为
的两根（终边不共线），求
的值
１３．已知函数图象y=
上相邻的最高点与最低点的坐标分别为
，求该函数的解析式．
§４－８三角函数的性质
一．选择题：
1．下列函数中同时满足下列条件的是（ ）
①在
上是增函数 ②以
为周期 ③是奇函数
2．如果
且
，则（ ）
3。已知
且
，则
可表示成（ ）
4．若
，则
的值是（ ）
（
不确定
5。下面函数的图象关于原点对称的是（ ）
6．函数
的取值范围是（ ）
二．填空题：
7．函数
的增区间为
8．设是以5为周期的函数，且当
时，
则
9．设
，其中
均为非零实数，若
，则
的值为
三．解答题：
１０．若
，试求
的解析式
１1．已知函数
（１） 求函数的定义域和值域
（２） 用定义判定函数的奇偶性
（３） 作函数在
内的图象
（４） 求函数的最小正周期及单调区间
１2．设函数的定义域为
（１） 求证：函数关于点
对称的充要条件是
（２） 若函数的图象有两个不同对称点，
，证明函数是周期函数．
§４－９ 三角函数的最值
一．选择题：
１．若
的最大值为M，最小值为N，则（ ）
２．在直角三角形中两锐角为
，则
的值（ ）
（A）有最大值和最小值0
（B）有最大值，但无最小值
（C）既无最大值也无最小值 （D）有最大值1，但无最小值
３．函数
，当
时的值域为（ ）
４．函数
，则此函数的最大值，最小值分别为（ ）
１．函数
在区间
上是增函数，且
，则
在区间上（ ）
（A）是增函数 （B）是减函数 （C）可取最大值2
（D）可取最小值
２．函数
的值域为（ ）
二．填空题：
３．函数
的定义域为值域为
４．函数
的最大值为
最小值为
５．设单位圆上的点
，求过点
斜率为的直线在ｙ轴上截距的最大值为
６．设直角三角形两个锐角为Ａ和Ｂ，则
的范围是
三．解答题：
７．求下列函数的最值
8已知关于ｘ的函数
的最小值为
，求 的解析式。13．设函数
的最大值为１，求实数
的值。
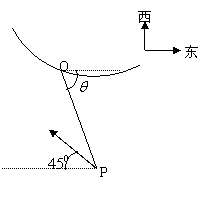
9在某海滨城市附近有一台风，据监测，当台风位于城市Ｏ（如图）的东偏南
方面的
海面处，并以
的速度向西偏北
方向移动。台风侵袭范围为圆形区域，当前半径为
，并以
的速度不断增大，问几小时后该城市开始受到台风的侵袭？并会持续多长时间？
 |
三角函数单元测试题
一．选择题：
１．集合
与
的关系为（ ）
２．下列函数中周期为的奇函数是（ ）
３．函数
在下列区间上为增函数的是（ ）
４．将函数的图象上每点的横坐标缩小为原来的（纵坐标不变），再把所得图象向左平移
个单位，得到的函数解析式为（ ）
５．
的值为（ ）
６．已知为锐角，且
，则
的值为（ ）
７．若
，则为（ ）
８．函数
的最大值是（ ）
非以上答案
９．要得到函数
的图象，可以把函数
的图象（ ）
右移 右移 左移 左移
１０．若对任意实数，函数
在区间
上的值
出现不少于４次且不多于８次，则
的值为（ ）
或
或
二．填空题：
１１．等腰三角形底角的正弦与余弦的和为
，则顶角的弧度数为
1２．若为锐角，且
，则
１３．
的解集区间为
１４．下列命题中正确的序号为
（你认为正确的都写出来）
①
的周期为，最大值为
②若x是第一象限的角，则是增函数
③在中若
则
④
既不是奇函数，也不是偶函数
⑤
且
则
⑥
的一条对称轴为
三．解答题：
15.
化简
16 已知
是方程
的两个实根，
求
的值
17．已知函数
⑴求
的最小正周期
⑵确定函数的递减区间
⑶确定
的最大值与最小值，并写出对应的的集合
⑷该函数图象可由函数
图象经过怎样的变换得到？
18. 已知函数
的图象在y轴右侧的第一个最高点为
，与x轴在原点右侧的第一个交点
，求这个函数的解析式。
19．求证：
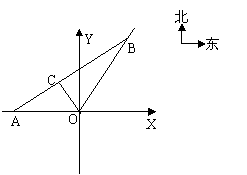
20．如图所示，某市现有自市中心O通往正西和东北方向的两条重要公路。为解决该市区交通拥挤问题，市政府决定修建一条环城公路。分别在到往正西和东北方向的公路上选取A．B两点，使环城公路A．Ｂ间为直线段．要求ＡＢ路段与市中心Ｏ的距离为１０公里，且使Ａ．Ｂ间的距离最小．试求Ａ，Ｂ两点的最短距离（不要求做近似计算）
 |
三角函数参考答案：
ξ４－１．任意角的三角函数．
１．Ｃ，２．Ｃ，３．Ａ，４．Ｂ，５．Ｂ，６．三，一或三，７．
８．
，９．二，１０．
或
，１２．０
ξ４－２．同角三角函数的基本关系及诱导公式．
１．Ａ，２．Ａ，３．Ｃ，４．Ａ，５．Ｂ，６．Ａ，７．
，８．
，９．０，１０．，
１１．⑴．
，⑵．
，１３．
１４．当是
第一象限角时为
，当是第三象限角时为
ξ４－３．两角和与差的三角函数．
１．Ｂ，２．Ａ，３．Ｂ，４．Ｄ，５．
，６．，７．
，８．２，９．１，１１．
ξ４－４．二倍角的正弦、余弦、正切．
１．Ｂ，２．Ｂ，３．Ｄ，４．Ｂ，５．Ａ，６．
，７．
，
８．
，９．
，１０．
，１１．１，１２．
ξ４－５．三角函数的化简与求值．
１．Ａ，２．Ｃ，３．Ｃ，４．Ｂ，５．Ａ，６．，７．
，８．
，９．
，１０．
或
，１１．
，１２．
，１３．
ξ４－７．三角函数的图象．
１．Ｄ，２．Ａ，３．Ｂ，４．Ｃ，５．Ｃ，６．，７．
，８．
，
９．２，１０．⑴．，⑵．
，⑶．左移
个单位，上移２个单位，⑷
．，
１１．⑴
，⑵．
，
１２．⑴．
，⑵．
，１３．
ξ４－８．三角函数的性质．
１．Ｃ，２．Ｃ，３．Ｄ，４．Ａ，５．Ｂ，６．Ｄ，７
，８．
，９．５，１０．
，
１１．⑴．定义域R，值域
，⑵．偶函数，⑷．周期，增区间 
，减区间
ξ４－９．三角函数的最值．
１．Ｃ，２．Ｂ，３．Ａ，４．Ｄ，５．Ｃ，６．Ｂ，７．定义域
，值域
，
８．
，９．，１０．
，１１．⑴．
，⑵．
１２．
，
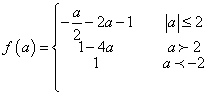
１３．
， １４．１４小时，持续１２小时
单元测试题．
选择题：１．Ｂ，２．Ｃ，３．Ｃ，４．Ｂ，５．Ｃ，６．Ａ，７．Ｂ，８．Ｂ，９．Ａ，１０．Ｄ
填空题：１１．
或
，１２．
，１３．
，１４．①③④⑤⑥
解答题：１５．
，
１６．
，
１７．⑴．
，⑵．
，⑶．当
时，的最小值为－５，当
时，的最大值为５，
１８．
２０．设，则
，则
,
令
而
整理得：
由
得：
此时
（符合条件）
故
即
最小值为