部分重点中学高三年级模拟考试

部分重点中学高三年级模拟考试

数学（理科）试卷

YCY

本试卷满分150分，考试用时120分钟.

参考公式：

①如果事件A、B互斥，那么P（A+B）=P（A）+P（B）　　　　  　　　　　　　

②如果事件A、B相互独立，那么P（A·B）=P（A）·P（B）　　　　　　　　　 

　　　 ③如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率　　　　

④球的表面积公式　（其中R表示球的半径）

　　　 ⑤球的体积公式　　 （其中R表示球的半径）

一、选择题：本大题共10小题，每小题5分；共50分.在每个小题给出的四个选项中，只有一项是符合题目要求的.

1．在下列各点中，不在不等式表示的平面区域内的点为　　　　　　　（ C　 ）

　　　 A．（0，1）　　　　　　　B．（1，0）　　　　　　 C．（0，2）　　　　　　　D．（2，0）

2．若函数）是奇函数，则下列坐标表示的点一定在函数图象上的是　　　　　　　　　　　　（ B　 ）

　　　 A．　　　　 B．　　　C．　　D．

3．复数Z+i在映射f下的象为·i，则－1+2i的原象为　　　　　　　　　　　　　　　　 （A　　）

　　　 A．2　　　　　　　　　　　　B．2－i　　　　　　　　　　C．－2+i　　　　　　　　　D．－1+3i

4．命题p:x=π是y=sinx的一条对称轴，q:2π是y=sinx 的最小正周期.下列复合命题：

　 ①p或q　　②p且q　　③非p　　④非q，其中真命题有　　　　　　　　　　　（　C  ）

　　　 A．0个　　　　　　　　　　B．1个　　　　　　　　　　C．2个　　　　　　　　　　D．3个

5．在的展开式中含项的系数是首项为－2，公差为3的等差

　 数列的　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　B  ）

　　　 A．第19项　　　　　　　B．第20项　　　　　　　C．第21项　　　　　　　D．第22项

6．椭圆=1的左、右焦点是F₁、F₂，P是椭圆上一点，若PF₁=3PF₂，则P点到左

　 准线的距离是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　C  ）

　　　 A．2　　　　　　　　　　　　B．4　　　　　　　　　　　　C．6　　　　　　　　　　　　D．8

7．设m，n是两条不同的直线，是两个不同的平面，则下面四个命题：

　　　 ①　　　　②

　　　 ③　 ④；

　　　 其中正确的命题是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　 D ）

　　　 A．仅①　　　　　　　　　 B．仅②　　　　　　　　　 C．①②③　　　　　　　 D．①③④

8．曲线y=x(x－1)(x－2)…(x－50)在原点处的切线方程为　　　　　　　　　　　　　　　　 （　D  ）

　　　 A．y=1275x　　　　　　　B．y=50²x　　　　　　　　C．y=100x　　　　　　　 D．y=50!x

9．在半径为10cm的球面上有A、B、C三点，如果AB=8，∠ACB=60°，则球心O到

　 平面ABC的距离为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　C  ）

　　　 A．2cm　　　　　　　　　　B．4cm　　　　　　　　　 C．6cm　　　　　　　　　　D．8cm

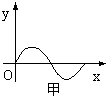
10．已知函数的导函数的图象如图甲所示，

　 则的图象可能是：（　D　）

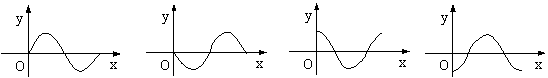　　　  A　　　　　　　　　 B　　　　　　　　　 C　　　　　　　　　 D

二、填空题：本大题共6小题，每小题4分，共24分.把答案填在题中横线上.

11．　 －1　　　　 .

12．已知点和向量，若，则点的坐标为　（7，5）　　　　。

13．在正方体ABCD—A₁B₁C₁D₁中，CC₁中点为E，则AE与BC₁所成的角的大小为　　45　　　 .

14．某城市的绿化建设有如下统计数据：

年　份	2002	2003	2004	2005
绿化覆盖率（%）	17.0	17.8	18.6	19.4

如果以后的几年继续依此速度发展绿化，那么使该城市的绿化覆盖率超过23.5%的最早

年份是　2011　　　　　　　  .

15．不等式的解集为　 {xx>1或x<－1}　

16．在酒泉卫星发射场某试验区，用四根垂直于地面的　　

　　　立柱支撑着一个平行四边形的太阳能电池板，可测

　　　得其中三根立柱、、的长度分别为

　　　、、，则立柱的长度是______25m_____.

16．设立柱的长度的长是，则，即

三、解答题（本大题共6小题，共76分，解答写出文字说明、证明过程或演算步骤）

17．（本小题满分12分）

　　已知△ABC中，角A、B、C对应的边为a、b、c，A=2B，cosB=.

　 （1）求sinC的值；

　 （2）若角A的内角平分线AD的长为2，求b的值.

解：（1）　　　　　　　　　　　　　　　　 …………2分

　　　　　　　　　　　　　　　　　　　　　　　…………4分

　　　　　　　　　　　　　　　　　　　　　　　 …………6分

　　　　　　　　　…………8分

（2）在△ACD中，∵A=2B，∴∠ADC=A，由正弦定理得

　 …………12分

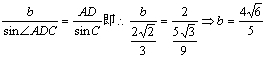18．（本小题满分12分）

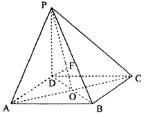
　　　 已知ABCD是正方形，PD⊥平面ABCD，PD=AD=2.

　 （Ⅰ）求PC与平面PBD所成的角；

　 （Ⅱ）求点D到平面PAC的距离；

　

解法一：

　 （Ⅰ）设AC与BD相交于点O，连接PO。

∵ABCD是正方形，∴AC⊥BD。

又∵PD⊥平面ABCD，∴PD⊥AC。

∵BD∩PD=D，　∴AC⊥平面PBD。

∴∠CPO为PC与平面PBD所成的角。

∵PD=AD=2，则OC=，PC=2。

在Rt△POC中，∠POC=90°，

∴

∴PC与平面PBD所成的角为30° …………6分

 （Ⅱ）过D做DF⊥PO于F，∵AC⊥平面PBD，

DF平面PBD， ∴AC⊥DF。

又∵PO∩AC=O， ∴DF⊥平面PAC。

在Rt△PDO中，∠PDO=90°，

∴PO·DF=PD·DO。

∴　…………12分

19．（本小题满分13分）

如图，在一个木制的棱长为3的正方体的表面涂上颜色，将它的棱3等分，然后从等分点把正方体锯开，得到27个棱长为1的小正方体。将这些小正方体充分混合后，装入一个口袋中.

　　　 （Ⅰ）从这个口袋中任意取出1个小正方体，这个小正方体的表面恰好没有涂颜色的概率是多少？

（Ⅱ）从这个口袋中同时任意取出2个小正方体，其中1个小正方体恰好有1个面涂有颜色，另1个小正方体至少有2个面涂有颜色的概率是多少？

解：在27个小正方体中，恰好3个面都涂有颜色的共8个，恰好2个面涂有颜色的

共12个，恰好1个面涂有颜色的共6个，表面没有涂颜色的1个.

（Ⅰ）从27个小正方体中任意取出1个，共有种等可能的结果.………3分

∵在27个小正方体中，表面没有涂颜色的只有1个，

∴从这个口袋中任意取出1个小正方体，这个小正方体的表面恰好没涂颜色的概率是

………………6分

（Ⅱ）从27个小正方体中，同时任取2个，共有种等可能的结果. 在这些结果中，

有1个小正方体恰好有1个面涂有颜色，另1个小正方体至少有2个面涂有颜色包含

的结果有种. ………………………………10分

∴从这个口袋中同时任意取出2个小正方体，其中1个小正方体恰好有1个面涂有颜

色，另1个小正方体至少有2个面涂有颜色的概率是

…………13分

 20.（本题满分12分）

　　　 设.

　 （1）求函数的单调区间；

　 （2）当时, 恒成立, 求实数的取值范围.

　　　 解：（1） ………（2分）

令或………（3分）

令………（4分）

在上为单调增函数………（5分）

在上为单调减函数………（6分）

（2） 令………（7分）

又, 且在上为单调增函数………（8分）

在上为单调减函数………（9分）在时,有极大值,

, 又………（11分）

………（12分）

21．（本小题满分13分）

　　已知数列{a_n}的前n项和S_n=(n+1)b_n, 其中{b­_n­}是首项为1，公差为2的等差数列

　 （1）求数列{a_n}的通项公式；

　 （2）若

_{解：（I）由已知，……2分}

_当

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 …………6分

（II）　 　　　　　…………8分

…………10分

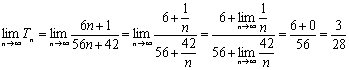　 　　 …………13分

22.（本小题满分14分）

已知

　　（1）求点的轨迹C的方程；

　　（2）若直线与曲线C交于A、B两点，并且A、B在y轴的异侧，求实数k的取值范围.

解析（1）由…………2分

又……4分

，故所求的轨迹方程是……7分

　 (2) 设、，把，得

…11分

∵A、B在y轴的异侧，，得到…………13分

综上，得.…………14分