长外2006届高三第三次月考试卷(文) 2005-10-31
时间:120分钟 满分150分
一 ![]() 选择题:本大题共10小题,每小题5分,共50分
选择题:本大题共10小题,每小题5分,共50分 ![]()
1 ![]() 已知集合
已知集合![]() 则AÇB等于
则AÇB等于
A ![]() F B
F B ![]()
![]() C
C ![]()
![]() D
D ![]()
![]()
2 ![]() 已知等差数列{an}的前
已知等差数列{an}的前![]() 项和为Sn,若a4=18-a5,则S8等于
项和为Sn,若a4=18-a5,则S8等于
A ![]() 18
B
18
B ![]() 36
C
36
C ![]() 54
D
54
D ![]() 72
72
3 ![]() 定义在R上的函数f(x)对任意两个不相等实数a,b,总有
定义在R上的函数f(x)对任意两个不相等实数a,b,总有![]() 成立,则必有
成立,则必有
A ![]() 函数f(x)是先增加后减少
B
函数f(x)是先增加后减少
B ![]() 函数f(x)是先减少后增加
函数f(x)是先减少后增加
C ![]() f(x)在R上是增函数
D
f(x)在R上是增函数
D ![]() f(x)在
f(x)在![]() 上是减函数
上是减函数
4 ![]() 命题A:x-1<3,命题B:(x+2)(x+a)<0且A是B的充分而不必要条件,则a的取值范围是
命题A:x-1<3,命题B:(x+2)(x+a)<0且A是B的充分而不必要条件,则a的取值范围是
A ![]() (4,+¥) B
(4,+¥) B ![]()
![]() C
C ![]() (-¥,-4) D
(-¥,-4) D ![]()
![]()
5 ![]() f(x)=ax
f(x)=ax![]() +3x
+3x![]() +2,若f¢ (-1)=3,则a的值等于
+2,若f¢ (-1)=3,则a的值等于
A ![]() 3
B
3
B ![]() 2
C
2
C ![]() 1
1 ![]() 5 D
5 D ![]() 4
4
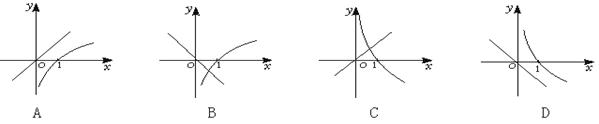
6 ![]() 当a>1时,函数y=logax和y=(1-a)x的图象只能是
当a>1时,函数y=logax和y=(1-a)x的图象只能是
7 ![]() 已知-9,a1,a2,-1四个实数成等差数列,-9,b1,b2,b3,-1五个实数成等比数列,则
已知-9,a1,a2,-1四个实数成等差数列,-9,b1,b2,b3,-1五个实数成等比数列,则![]()
A ![]() 8 B
8 B ![]() -8 C
-8 C ![]() ±8 D
±8 D ![]()
8 ![]() 下列判断错误的是
下列判断错误的是
A
![]() 命题“若q则p”为真命题,则
命题“若q则p”为真命题,则![]() 为
为![]() 成立的必要条件
成立的必要条件
B
![]() “
“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
C
![]() 命题“若
命题“若![]() ,
,![]() 方程
方程![]() 的根,则
的根,则![]() 或
或![]() ”的否命题为“若
”的否命题为“若![]() ,
,
![]() 不是方程
不是方程![]() 的根,则
的根,则![]() 且
且![]() ”
”
D ![]() 命题“
命题“![]() 且
且![]() ”为真命题
”为真命题
9 ![]() 已知定义在R上的奇函数f(x),对任意x值都有f(1+x)= f(1-x)成立,且当
已知定义在R上的奇函数f(x),对任意x值都有f(1+x)= f(1-x)成立,且当![]() 时f(x)=x2+x,则f(10
时f(x)=x2+x,则f(10 ![]() 5)值等于
5)值等于
A ![]()
![]() B
B ![]()
![]() C
C ![]() 0 D
0 D ![]() —2
—2
10 ![]() 已知函数f(x)满足
已知函数f(x)满足![]() ,且
,且![]() ,设有数列
,设有数列![]() ,
,![]() 为任意实数),则
为任意实数),则
A ![]()
![]() 与
与![]() 均成等比数列
B
均成等比数列
B ![]()
![]() 与
与![]() 均成等差数列
均成等差数列
C ![]()
![]() 成等比数列,
成等比数列,![]() 成等差数列
D
成等差数列
D ![]()
![]() 成等差数列,
成等差数列,![]() 成等比数列
成等比数列
二 ![]() 填空题:本大题共5小题,每小题4分,共20分
填空题:本大题共5小题,每小题4分,共20分
![]()
11
![]() 曲线
曲线![]() 在点
在点![]() 处的切线的切线方程___________
处的切线的切线方程___________ ![]()
12 ![]() Sn=12 -22+32
-42+…+(2n -1)2
-(2n)2=______________;
Sn=12 -22+32
-42+…+(2n -1)2
-(2n)2=______________;
13 ![]() 已知函数f(x)=ax+2a+1,当x
已知函数f(x)=ax+2a+1,当x![]() [-1,1]时,f(x)有正值也有负值,则实数a的取值范围是__________;
[-1,1]时,f(x)有正值也有负值,则实数a的取值范围是__________;
14 ![]() 设
设![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() _______________
_______________ ![]()
15 ![]() 把下面不完整的命题补充完整,能使之成为真命题的是
把下面不完整的命题补充完整,能使之成为真命题的是
![]()
若函数![]() 的图象与
的图象与![]() 的图象关于
对称,则函数
的图象关于
对称,则函数![]() =
=
![]() ①x轴,
①x轴,![]() ②y轴,
②y轴,![]() )
)
③原点,![]() ④直线
④直线![]()
(注:填上你认为可以成为真命题的一种情形即可,不必考虑所有可能的情形)
答题卷(文科) 姓名 学号 得分
一 ![]() 选择题(50分)
选择题(50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二,填空题(20分)
11 ![]() 12
12 ![]() 13
13 ![]()
14 ![]() 15
15 ![]()
三 ![]() 解答题:本大题共6小题,共80分
解答题:本大题共6小题,共80分
![]() 解答应写出文字说明,证明过程或演算步骤
解答应写出文字说明,证明过程或演算步骤 ![]()
16 ![]() (12分)设
(12分)设![]()
![]()
(1)若![]() ,求
,求![]() 的值; (2)若
的值; (2)若![]() ,求
,求![]() 的值
的值 ![]()
17 ![]() (12分) 已知函数f(x)=3x+1+9x-12的反函数是f-1 (x)
(12分) 已知函数f(x)=3x+1+9x-12的反函数是f-1 (x)
(1) 求f -1 (6) 的值; (2)要使f -1 (a)有意义,求a的取值范围 ![]()
18 ![]() (14分)已知
(14分)已知![]() 是等差数列,
是等差数列,![]() 是等比数列,且
是等比数列,且![]()
![]() ,
,![]() ,又
,又![]()
![]()
![]() (1)求数列
(1)求数列![]() 的通项公式和数列
的通项公式和数列![]() 的通项公式;
的通项公式;
(2)设![]() ,其中
,其中![]() ,求
,求![]() 的值
的值 ![]()
19 ![]() (14分)已知数列
(14分)已知数列![]() 的前
的前![]() 项和为
项和为![]()
![]()
(1)试写出![]() 中
中![]() 与
与![]() 的关系式,并求数列
的关系式,并求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,如果对一切正整数
,如果对一切正整数![]() 都有
都有![]() ,求
,求![]() 的最小值
的最小值 ![]()
20 ![]() (14分) 轻纺城的一家私营企业主,一月初向银行贷款一万元作开店基金,每月月底获得的利润是该月初投入资金的
(14分) 轻纺城的一家私营企业主,一月初向银行贷款一万元作开店基金,每月月底获得的利润是该月初投入资金的![]() ,每月月底需要交纳房租和所得税为该月所得金额(包括利润)的
,每月月底需要交纳房租和所得税为该月所得金额(包括利润)的![]() ,每月的生活费开支300元,余款作为资金全部投入再经营,如此继续,问该年年底,该私营企业主有现款多少元?如果银行贷款的年利率为
,每月的生活费开支300元,余款作为资金全部投入再经营,如此继续,问该年年底,该私营企业主有现款多少元?如果银行贷款的年利率为![]() ,问私营企业主还清银行贷款后纯收入还有多少元?
,问私营企业主还清银行贷款后纯收入还有多少元?
21 ![]() (14分)已知
(14分)已知![]() 是函数
是函数![]() 的一个极值点,其中
的一个极值点,其中![]() ,
,
(1)求![]() 与
与![]() 的关系式;(2)求
的关系式;(2)求![]() 的单调区间;
的单调区间;
(3)若![]() ,求证:函数
,求证:函数![]() 的图象与
的图象与![]() 轴只有一个交点
轴只有一个交点 ![]()
数学(文科)参考答案
一 ![]() 选择题(50分)
选择题(50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | D | C | C | A | B | B | B | B | C |
二,填空题(20分)
11 ![]()
![]() 12
12 ![]()
![]() 13
13 ![]()
![]()
14 ![]() 0
15
0
15 ![]() ④,
④,![]() 或①,
或①,![]()
三,解答题;
16解;∵![]()
![]()
(1)![]() ,①若
,①若![]()
![]() ,则△=
,则△=![]()
②若![]()
若![]() ,此时
,此时![]() 无解
无解
若![]()
若![]()
综上;![]()
(2)![]()
∵ ![]()
17解;(1)∵![]()
则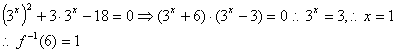
(2)要使![]() 有意义,则
有意义,则![]() 有解
有解
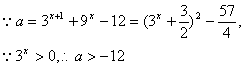
18解;(1)![]() 是等比数列,且
是等比数列,且![]() ,则公比
,则公比![]()
![]()
![]() 等差,设公差为
等差,设公差为![]() ,首项为
,首项为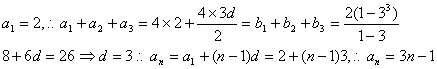
(2)∵![]() 等比,∴
等比,∴![]() 也成等比,且公比为
也成等比,且公比为![]()
∴![]()
19 解;(1)∵![]() ① ∴
① ∴![]() ②
②
①-②得;![]()
∴![]() 等差,且首项2为,公差为2 ∴
等差,且首项2为,公差为2 ∴![]()
(2)由(1)知![]()
∵![]() 恒成立,则
恒成立,则![]()
又![]() ,当
,当![]() 时
时![]() ,当
,当![]() 时,
时,![]()
当![]() 时
时 ![]() 当
当![]() 时,
时,![]()
∴![]()
20解;有现款略为19488 ![]() 6元,还贷后纯收入为8988
6元,还贷后纯收入为8988
![]() 6元
6元
21略解;(1)![]()
(2)递增区间为![]() ,递减区间为
,递减区间为![]()
(3)证明略